
今回は”惑星トンネル”の問題です.惑星の中心を通るように穴を掘って物体を落とす話しです.リオオリンピックの閉会式でマリオが土管を設置して惑星トンネルをつくっていたね.(動画はきえてしまっているようです。)

でも惑星の内部に入ると何か変わるの?

惑星の中心にいくほど万有引力が小さくなります.やがて中心にたどり着くと,万有引力がほぼ0となります.

地球の質量は変わらないのに?
たしか,質量をもっているもの同士は万有引力がはたらくんだったよね.
質量$m$と質量$M$の重心間の距離を$r$とする.万有引力定数を$G$とすると,万有引力の大きさ$F$は
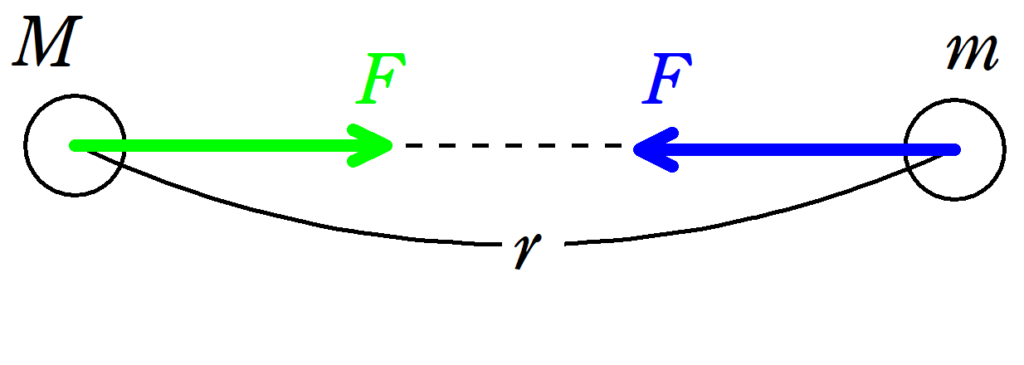
$F=G\dfrac{Mm}{r^2}$
となります.

実は,惑星の内部にいる場合,自分より外側にある質量の分の万有引力は受けないんです.たとえば,下図であったら,惑星Xの表面にいる赤の人は半径$R$の惑星Xの質量分の万有引力を受けますが,惑星Xの内部にいる青い人は,内側の緑の斜線部分の質量の万有引力しか受けません.
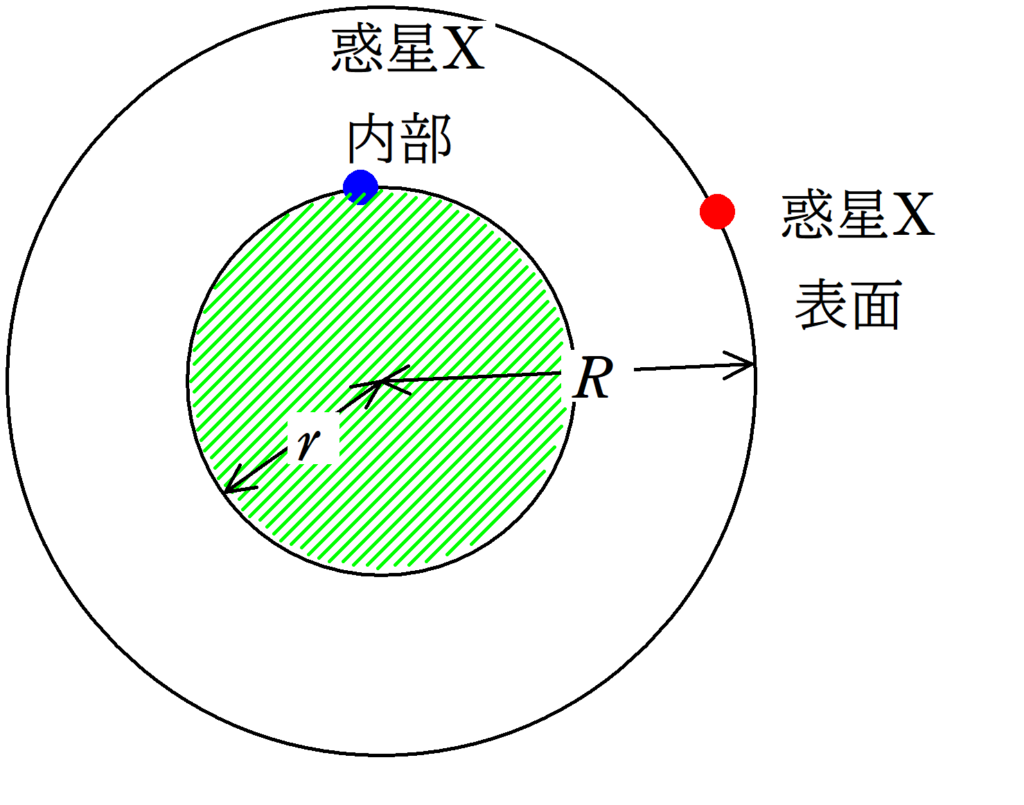

不思議!外側の万有引力は受けないんだ.なんで・・・?

それでは,まず薄い球殻を考えてみましょう.球の風船をイメージしてもらえればいいです.風船の内部にある物体と風船の膜部分との万有引力の和が0になったら,地球の内部に物体があるとき,物体の外側の地球の質量分の万有引力は0であることがわかります.
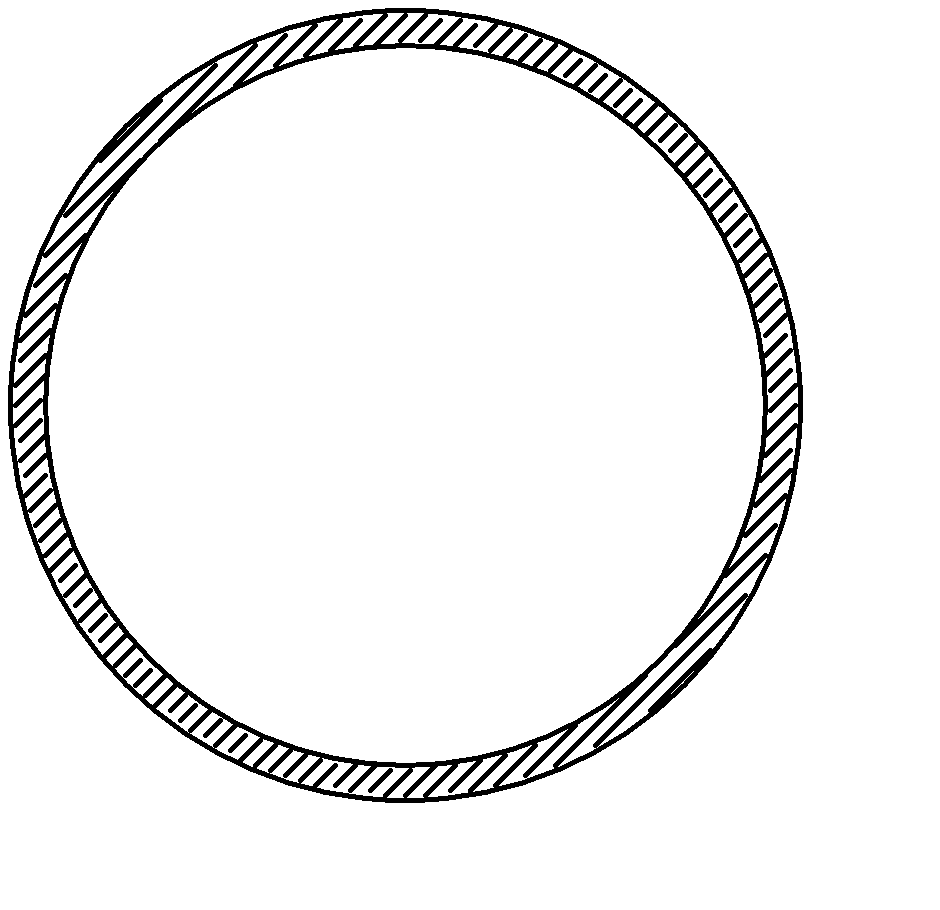

外側は薄い膜を集めたものだからね.
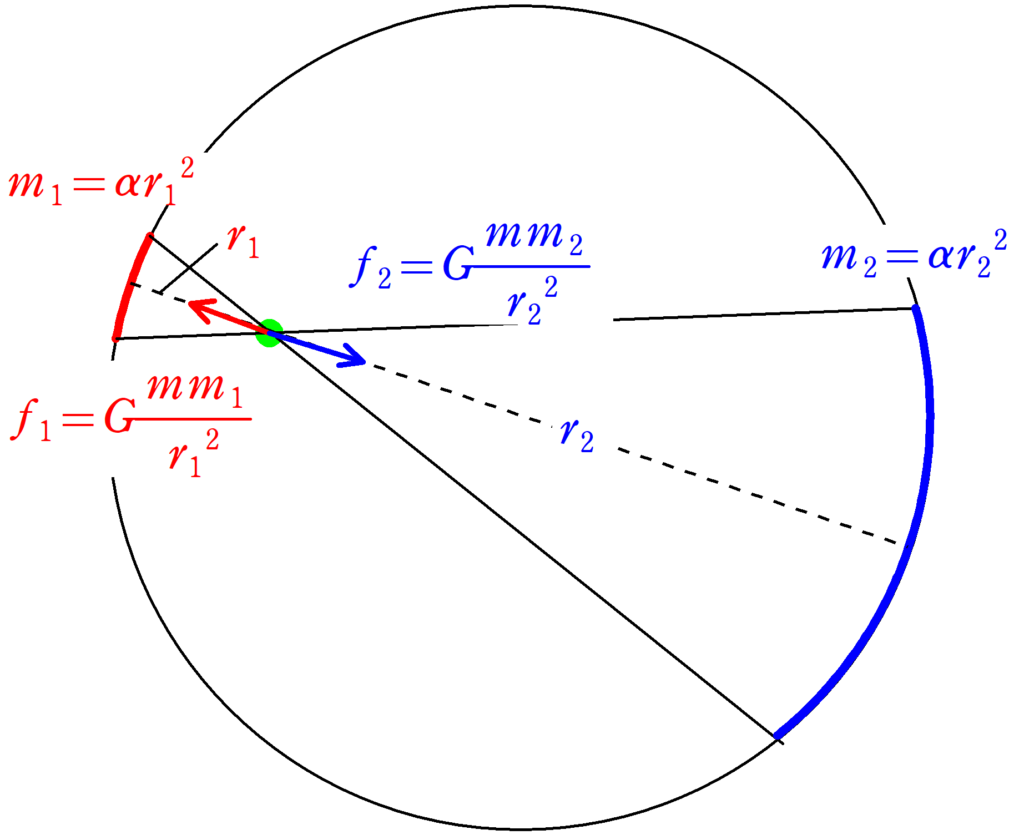
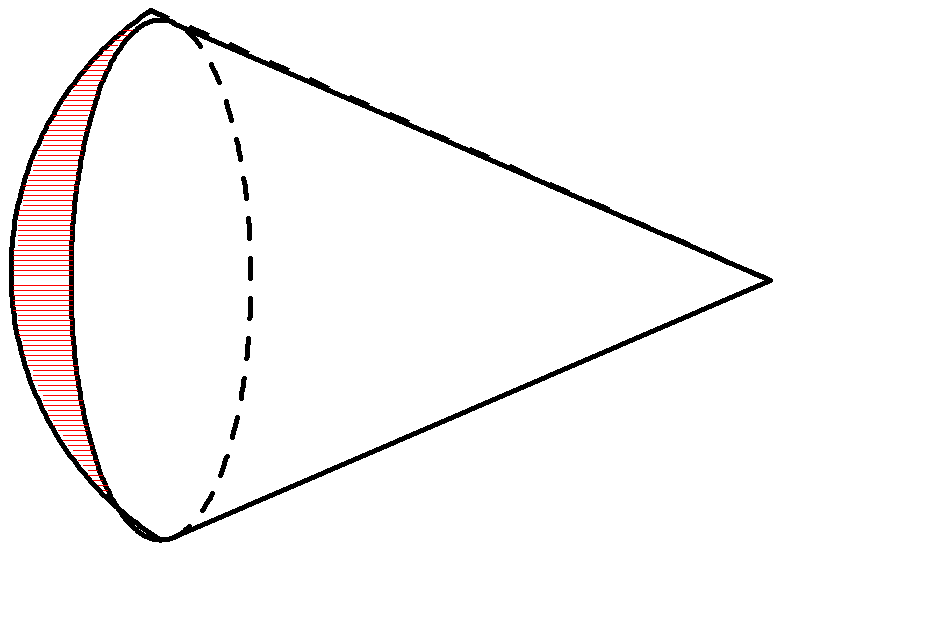

球殻の内部にある質量$m$の緑の物体について考えます.そこで,上図の球殻の赤い部分と青い部分の質量がおよぼす緑の物体の万有引力を計算してみます.緑の物体から赤い部分,青い部分との距離は$r_{1}$,$r_{2}$です.また,赤い部分と青い部分のそれぞれの端と緑の物体を結ぶと,相似な図形ができます.
赤の図形と青の図形相似比は$r_{1}:r_{2}$になるので,面積比は$r_{1}^2:r_{2}^2$ですね.なので,比例定数$\alpha$を使って,赤い方の質量を$m_{1}=\alpha r_{1}^2$,青い方の質量を$m_{2}=\alpha r_{2}^2$としましょう.
その上で赤い方が緑に及ぼす万有引力の大きさ$F_{赤\rightarrow 緑}$と青い方が緑に及ぼす万有引力の大きさ$F_{青\rightarrow 緑}$はそれぞれ次のようになります.
$\eqalign{F_{赤\rightarrow 緑}&=G\dfrac{mm_{1}}{r_{1}^2}\\&=G\dfrac{m\alpha \cancel{r_{1}^2}}{\cancel{r_{1}^2}}\\&=Gm\alpha}$
$\eqalign{F_{青\rightarrow 緑}&=G\dfrac{mm_{2}}{r_{2}^2}\\&=G\dfrac{m\alpha \cancel{r_{2}^2}}{\cancel{r_{2}^2}}\\&=Gm\alpha}$

$F_{赤\rightarrow 緑}$と$F_{青\rightarrow 緑}$は力の向きが逆だから打ち消すんだ!
ということは下のように,打ち消す対になる球殻部分があるってことかな?赤の部分も打ち消すし,青の部分も打ち消す,黄色の部分も打ち消す.
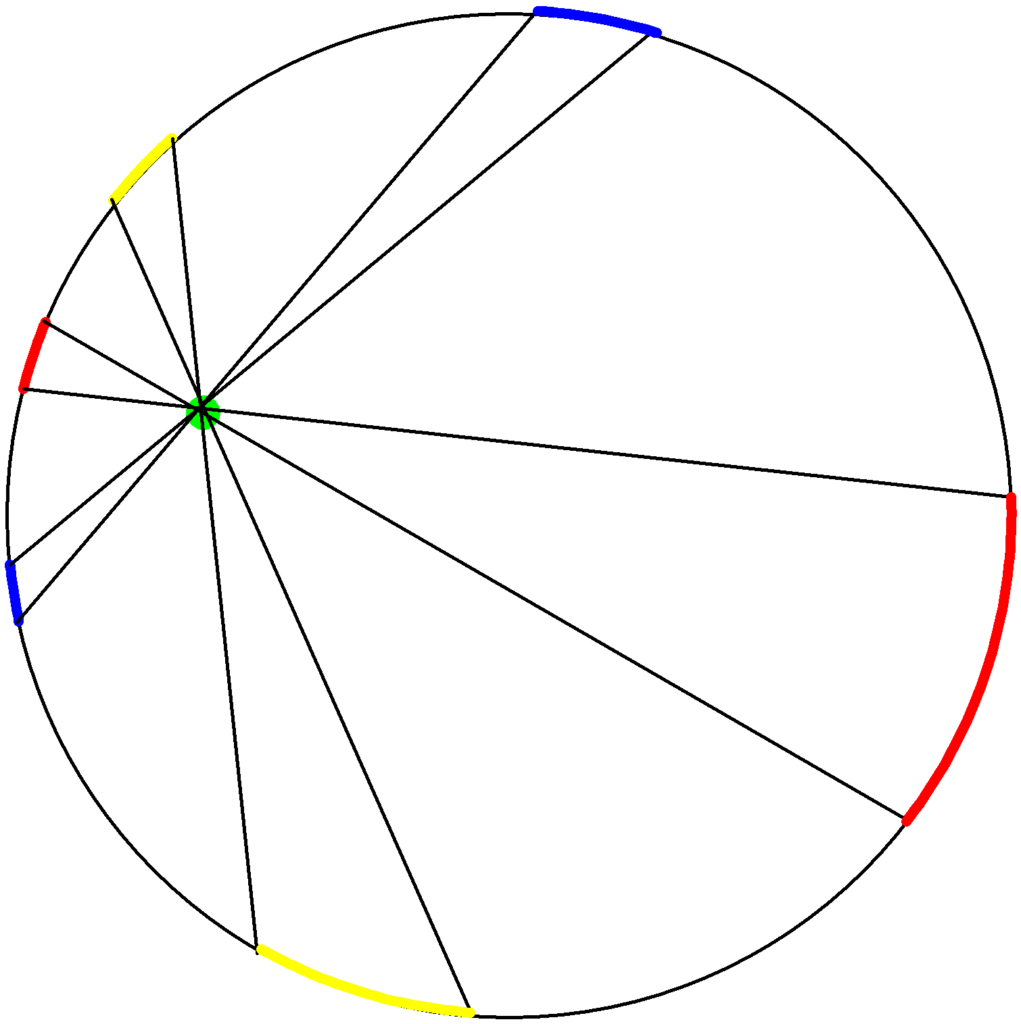

そういうことです.結論,惑星内部の物体にはたらく万有引力は惑星を中心とした物体を通る部分の球の質量分しかはたらかない,ということです.

なるほど!じゃあ早速問題を解いてみよう!
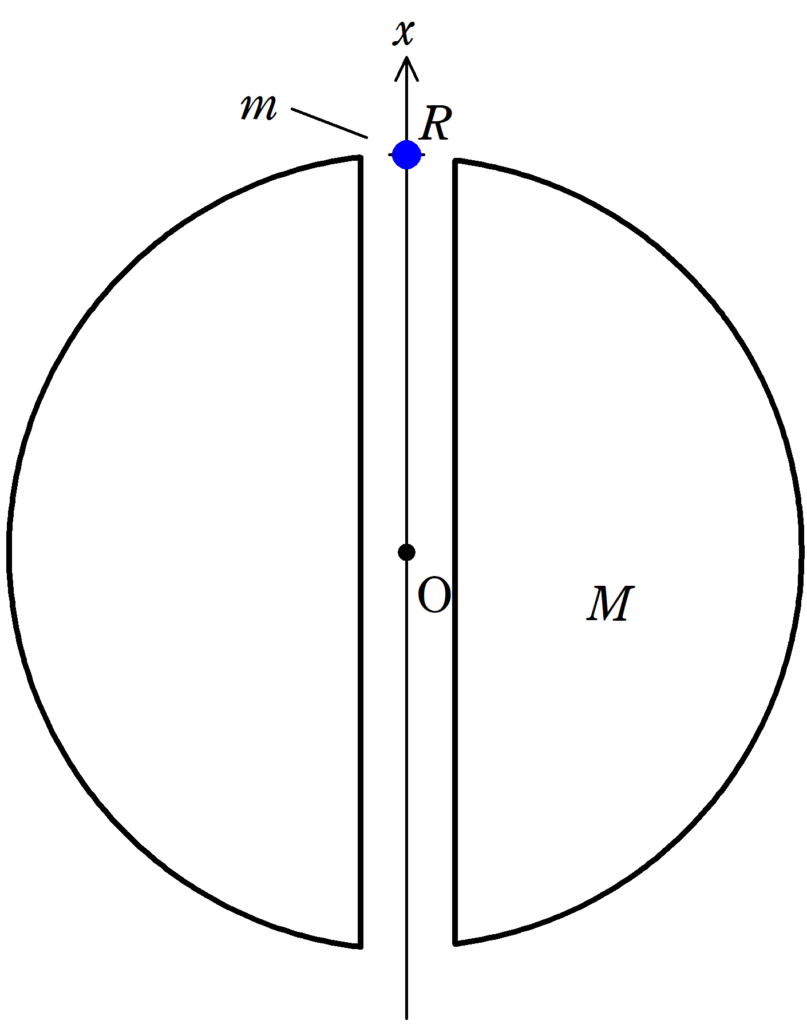
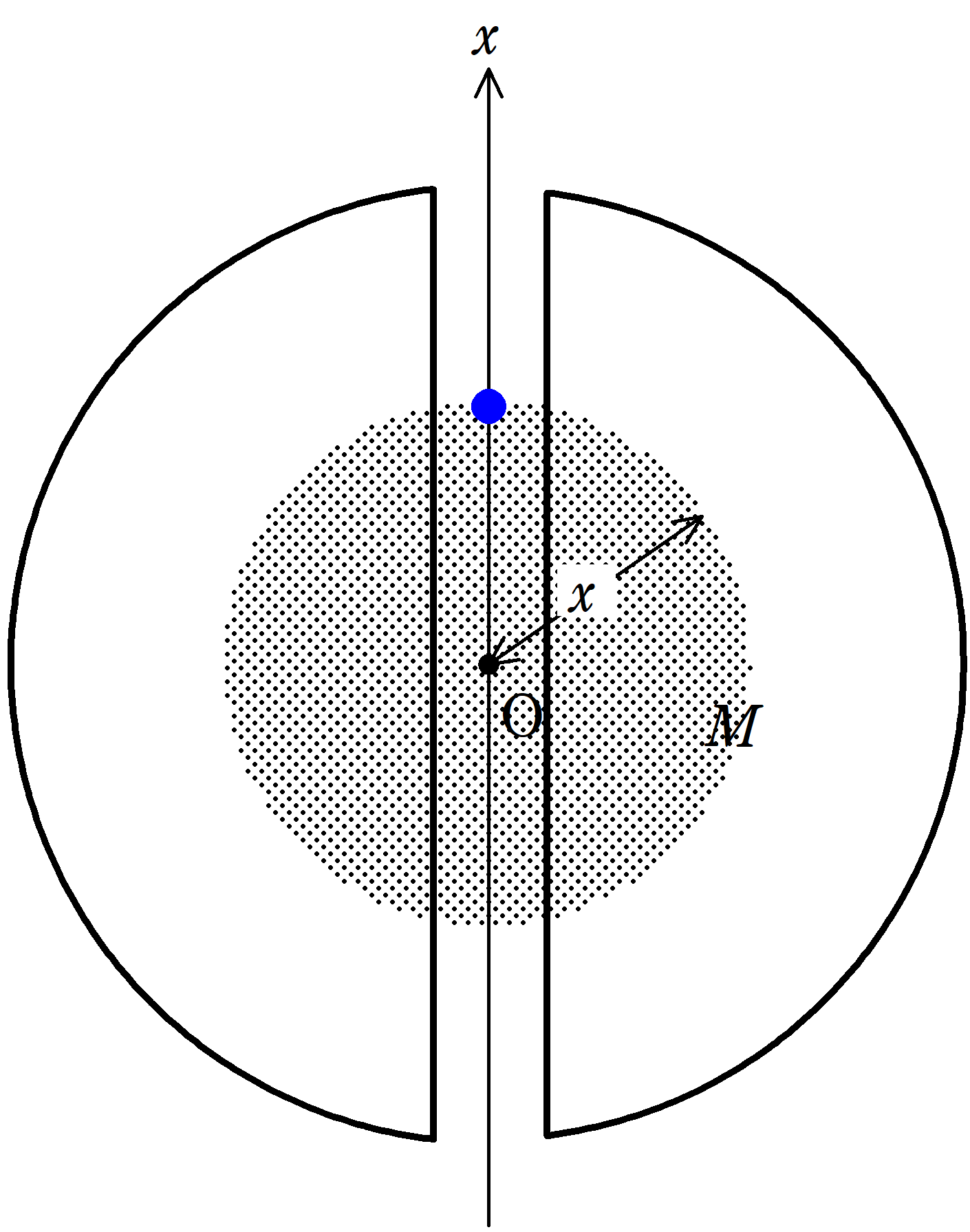
質量$M$,半径$R$で一様な密度の惑星Xがある.惑星Xは自転をしていないものとする.惑星Xの表面から中心を通るように穴を掘り,反対側まで貫通させる.惑星Xの中心を座標の原点Oとし,上図の向きに$x$座標をとる.惑星Xの表面$x=R$に質量$m$の物体おき,時刻$t=0$で静かにはなしたところ,物体は惑星Xとは衝突をせず落下運動をはじめた.物体のその後の運動について次の問いに答えよ.ただし,万有引力定数を$G$とし,空気抵抗は無視をする.また,惑星X内部の物体にはたらく万有引力は惑星Xを中心とした物体を通る部分の球の質量分しかはたらかない.
(1) $0\leqq x\leqq R$のときに物体にはたらく万有引力を$G$,$M$,$m$,$R$,$x$を用いて表せ.
(2) $-R\leqq x\leqq 0$のときに物体にはたら万有引力を$G$,$M$,$m$,$R$,$x$を用いて表せ.
(3) $t>0$において,物体の位置が$x$であるときの加速度を$x$軸の正の向きに$a$とする.このときの物体の運動方程式を$a$,$G$,$M$,$m$,$R$,$x$を用いて立式せよ.
(4) 物体の単振動の中心$x_{0}$,振幅$A$,角振動数$\omega_{0}$,周期$T$を$G$,$M$,$m$,$R$から必要なものを用いて表せ.
(5) 時刻$t$における物体の位置$x$を$G$,$M$,$m$,$R$,$t$を用いて表せ.
(6) 物体の中心における速さを求めよ.
<解答>
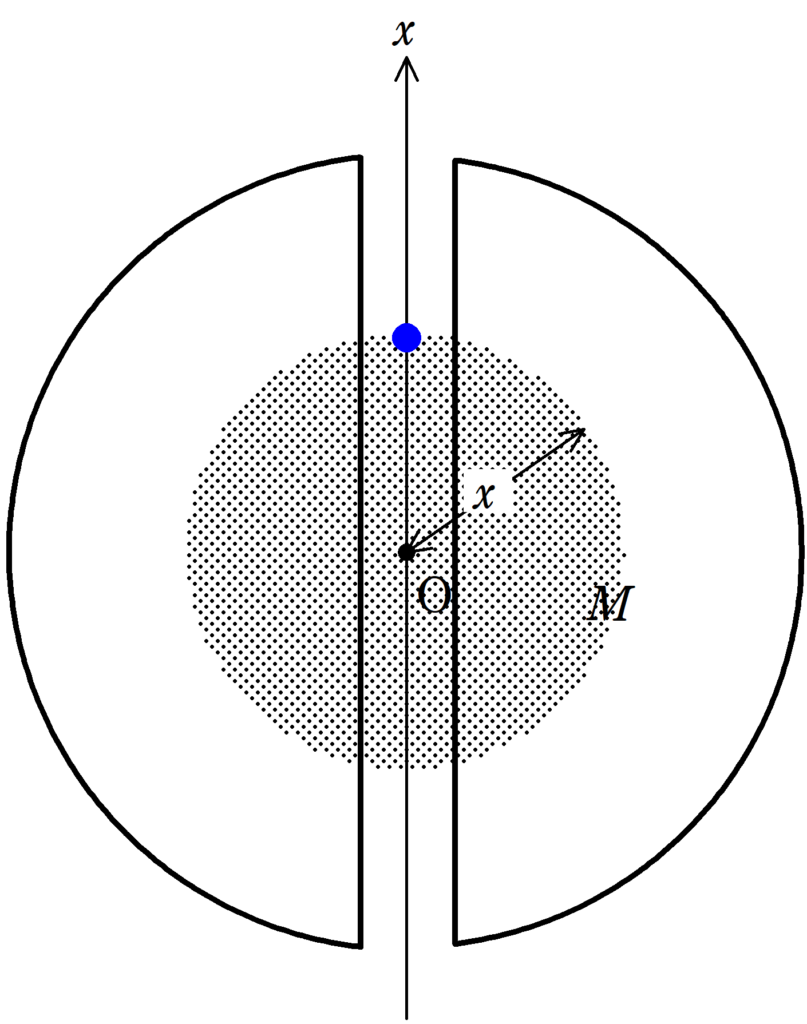
(1) 位置$0\leqq x\leqq R$にいる物体があるときは上図の黒色塗り部分の質量$M^{\prime}$の万有引力しかはたらきません.質量は体積に比例するので
$\eqalign{M:M^{\prime}&=\dfrac{4\pi R^3}{3}:\dfrac{4\pi |x|^3}{3}\cr M:M^{\prime}&=R^3: |x|^3\cr M^{\prime}&=\dfrac{|x|^3}{R^3}M\cr M^{\prime}&=\dfrac{x^3}{R^3}M}$
最後の式変形では,$x>0$であることから,$|x|=x$と絶対値をはずしました.
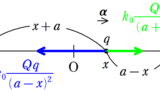
さて,求めるのは”万有引力”です.“万有引力の大きさ”ではありません.$x\leq 0$のときは,万有引力は惑星Xの中心である$x$軸の負の向きにかかることに注意して,万有引力$F_{+}$は
$\eqalign{F_{+}&=-G\dfrac{M^{\prime}m}{x^2}=-G\cdot \dfrac{x^3}{R^3}M \cdot \dfrac{m}{x^2}&=-\dfrac{GMm}{R^3}x}$
したがって,求める力は$F_{+}=-\dfrac{GMm}{R^3}x$となります.
(2) $-R\leqq x\leqq 0$のときは質量$M^{\prime}$は
$M^{\prime}=\dfrac{|x|^3}{R^3}M=-\dfrac{x^3}{R^3}M$
となります.$x<0$のとき,$|x|=-x$となるからですね.
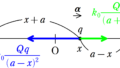
$x<0$における万有引力は$x$軸の正の向きなので,求める力$F_{-}$は
$\eqalign{F_{-}&=G\dfrac{M^{\prime}m}{x^2}=G\cdot (-\dfrac{x^3}{R^3}M) \cdot \dfrac{m}{x^2}&=-\dfrac{GMm}{R^3}x}$
したがって,求める力は$F_{-}=-\dfrac{GMm}{R^3}x$となります.

結局$0\leqq x$でも$x<0$でも力は$-\dfrac{GMm}{R^3}x$とあらわすことができるんだね!

そういうことです.
(3) (1),(2)より,位置$x$における運動方程式は
$ma=-\dfrac{GMm}{R^3}x$
(4) (3)の運動方程式より,振動の中心は$x_{0}=0$,角振動数は$\omega=\sqrt{\dfrac{GM}{R^3}}$,周期は$T=2\pi \sqrt{\dfrac{R^3}{GM}}=2\pi R\sqrt{\dfrac{R}{GM}}$です.また,$x=R$で速度0からスタートするので,この場所が上端,中心が$x=0$なので,上端と中心との距離は$R$となります.これが振幅ですね.$A=R$
(5) $x=R$から速度0でスタートして,$x$軸の負の方向にいくので,$\cos$型です.
$\eqalign{x&=x_{0}+A\cos \omega t \\&=R\cos \sqrt{\dfrac{GM}{R^3}}t}$
(6) 単振動のエネルギー保存で解いてみましょう.
$ma=-\dfrac{GMm}{R^3}x$
を変形して
$\dfrac{1}{2}mv^2+\dfrac{1}{2}\dfrac{GMm}{R^3}x^2=$一定
です.$x=R$のとき,$v=0$であって,中心である$x=0$のときの速さを$v=V$とすると上式より
$\eqalign{\dfrac{1}{2}m\cdot 0^2+\dfrac{1}{2}\dfrac{GMm}{R^3}R^2&=\dfrac{1}{2}mV^2+\dfrac{1}{2}\dfrac{GMm}{R^3}\cdot 0^2\cr \dfrac{1}{2}mV^2&=\dfrac{1}{2}\dfrac{GMmR^2}{R^3}\cr V^2&=\dfrac{GM}{R} \cr V&=\sqrt{\dfrac{GM}{R}}}$
したがって,求める速さは$V=\sqrt{\dfrac{GM}{R}}$です.

これなら,東京を$x=R$,リオを$x=-R$として,単振動をして$x=-R$の位置でリオにある土管につかまればうまくたどり着くことができるね!

実際は,自転をしているし,空気抵抗もあるからそううまくはいきませんけどね.理想的には確かにそうです.ところで,単振動の周期$T$はどのような値になるでしょうか.

(4)から$T=2\pi R\sqrt{\dfrac{R}{GM}}$だよね.惑星Xが地球だった場合$R=6.4×10^6 \rm{m}$と,$G=6.7×10^{-11} \rm{Nm^2/kg^2}$と,$M=6.0×10^{24} \rm{kg}$を代入して,約5000秒.つまり約83分,その半分だから40分少しでつくんだ!

はやいですね.かなり理想化した問題ですが,高校物理の問題を解くことでこのような面白い結果も得られるわけです.

コメント
[…] […]