
今回は共通テスト対策問題です!
電位の問題ですが,電位の公式はただ覚えているだけ,となっていませんか?
その確認として以下の問題を解いてみましょう.
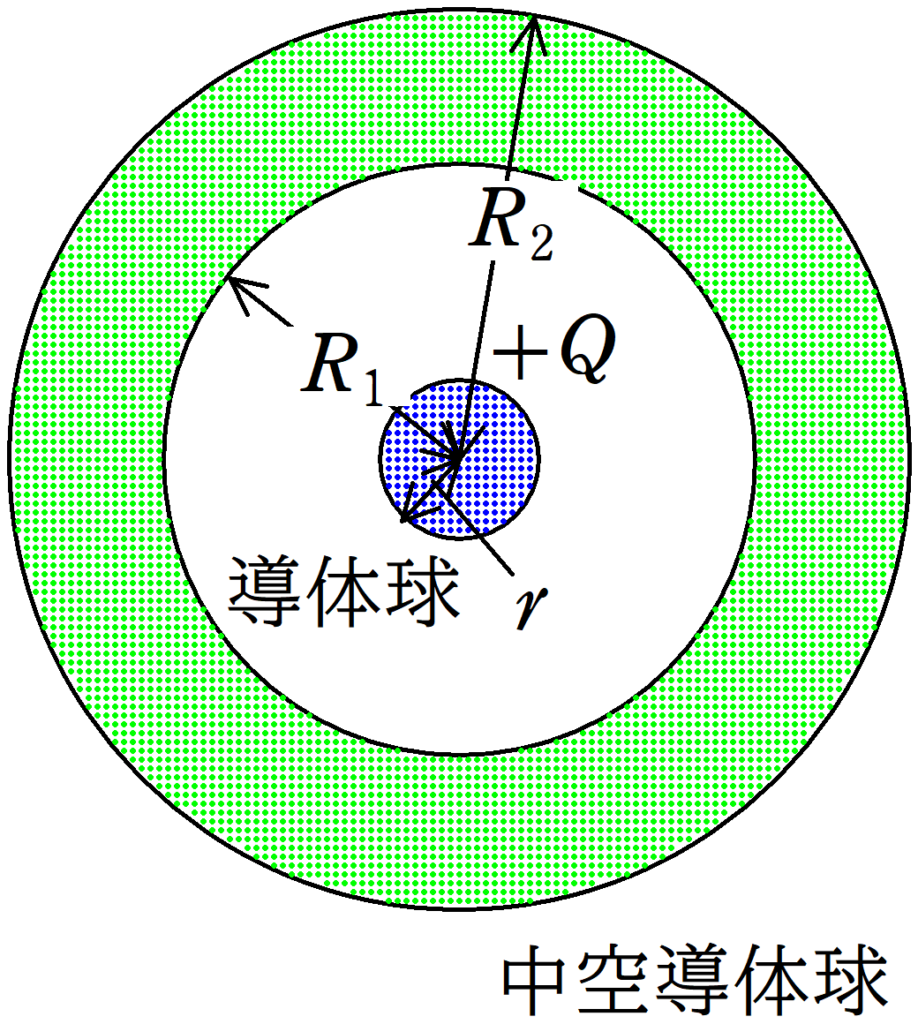
図のように,電気量$Q$$(Q>0)$の電荷が帯電している半径$r$の導体球の外側に,球心を一致させた内半径$R_{1}$,外半径$R_{2}$の帯電していない中空導体球を設置した.
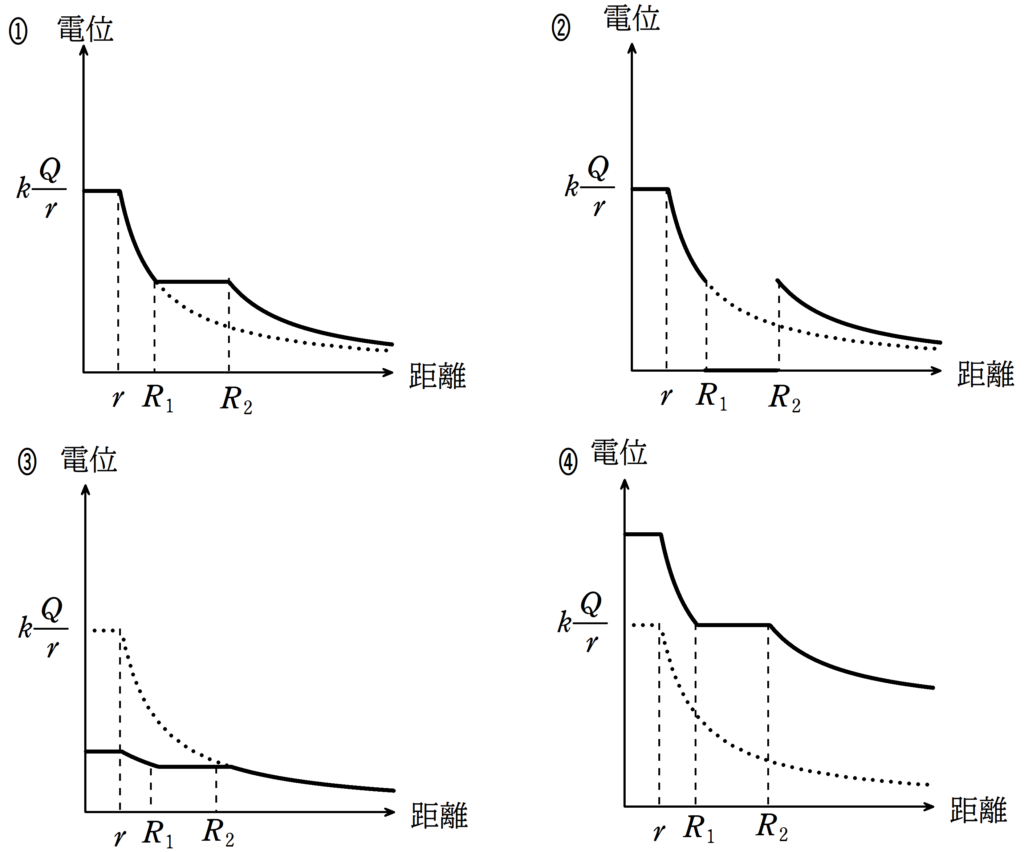
無限遠を基準としたときに導体球の中心からの距離と電位の関係を表したグラフとして最も適当なものを①~④の中から選べ.
ただし,グラフの点線で示されているものは中空導体球がない場合の距離と電位の関係であり,実線が中空導体球を設置したときの距離と電位の関係である.
また,点線部分が書かれていないところは実線と重なっていると考えてよい.

答えは一番最後にあります.(答えだけ見たい人は目次からとんでくだい)
さて,そもそも電位とは何かについて話しておきましょう.
電位とは何か
電位は1$\rm{C}$の電荷がもつ静電気力による位置エネルギーです.
無限遠を電位の基準とすると,点電荷$Q$が距離$r$の位置につくる電位$V$は
$V=k\dfrac{Q}{r}$
と表されます.電位の計算では$Q$に絶対値をとらないようにしましょう.
重力による位置エネルギーの例1
まずは,重力による位置エネルギーの復習です.
位置エネルギーは,物体をつり合わせながらゆっくりと動かしたときに外力が仕事をした分だけ蓄えられます.
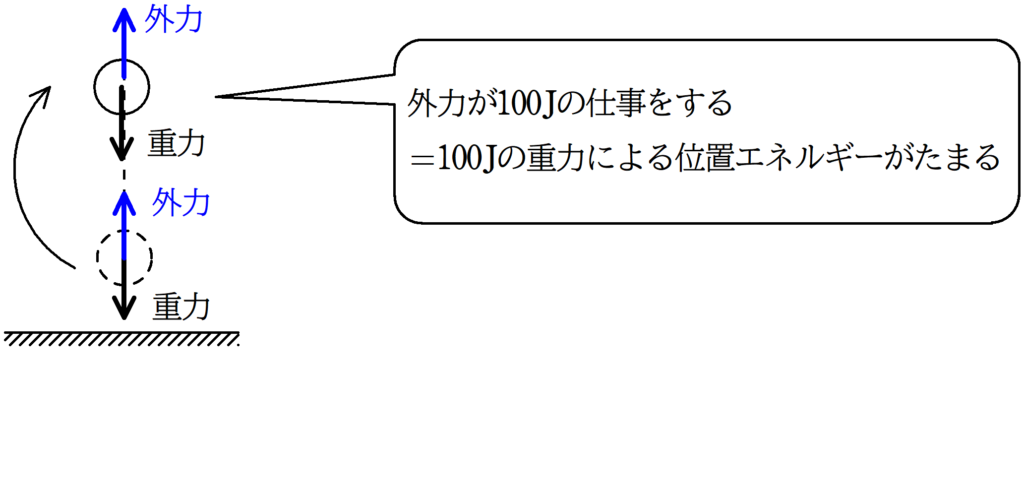
たとえば,重力がはたらいている状況で重力とは逆向きに重力と同じ力の外力を加えます.
そして,物体を外力の方向に動かすと外力が$100\rm{J}$の仕事をしました.
このとき,物体は$100\rm{J}$の位置エネルギーを蓄えます.
外力を加えるのをやめると,運動を開始します.
物体は運動エネルギーを得て,最初の位置と同じ場所につくころには$100\rm{J}$の運動エネルギーをもっています.
重力による位置エネルギーの例2
もし,外力が仕事をしなければ,位置エネルギーは変化しません.
たとえば,次のような場合です.
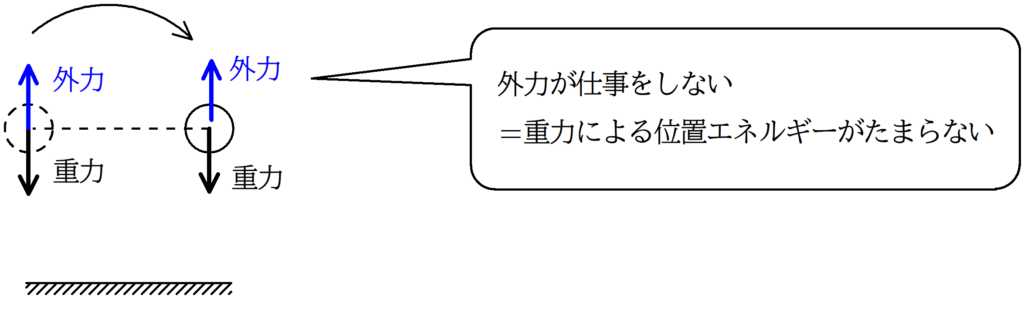
このとき,外力の加えた方向と垂直な方向に物体が動いているので,外力は仕事をしません.
すると位置エネルギーは蓄えられません.
まとめ 重力による位置エネルギーの計算の仕方
重力による位置エネルギーは基準点からゆっくりと動かす際に,外力がした仕事の分だけ蓄えられます.もし,外力が仕事をしなかったら重力による位置エネルギーは蓄えられません.
導体球と中空導体球によってつくられる電場を求める.
電位を計算するにはどのくらいの外力を加えて動かすのかを計算する必要があります.
なので,あらかじめ電場を計算しておく必要があります.
無数の点電荷があり,対称性がある→ガウスの法則
今回の問題では,導体球に電気量$Q$の電荷が蓄えれていますが,この電荷は導体球の表面に分布しています.
しかし,無数の電荷をベクトルの足し算で計算するのは困難です.(できなくはないですが)
そこで,便利なのガウスの法則です.ガウスの法則は特に次のような問題と相性がよいです.
点電荷が無数にある,電荷が分布している物体に対称性がある
今回はガウスの法則を使って電場の計算をしましょう.
ガウスの法則
電場の大きさを次のように決めます.
電場の大きさを$1\rm{m^2}$あたりに閉曲面を垂直に貫く電気力線の本数と決める.
電荷があるとまわりに電気力線をつくります.
電荷$Q$がつくる電気力線の本数$N$は誘電率を$\varepsilon_{0}$,クーロンの比例定数を$k_{0}$とすれば
$N=4\pi k_{0}|Q|=\dfrac{|Q|}{\varepsilon_{0}}$
です.
したがって,ガウスの法則より電場の大きさ$E$は
$E=\dfrac{N}{S}=\dfrac{4\pi k_{0}|Q|}{S}=\dfrac{|Q|}{\varepsilon_{0}S}$
ガウスの法則で電場を求める.
ガウスの法則を使う前に,電荷分布について確認しておきます.
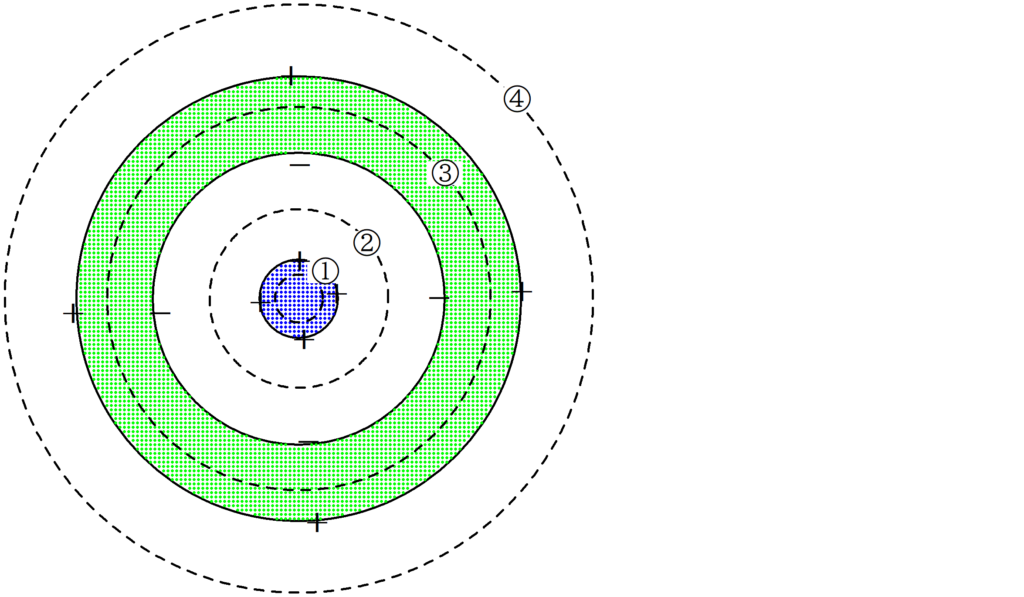
導体球の表面には電気量$+Q$が一様に分布しています.
もともと中空導体球は電荷0であったのですが,導体球の電荷にひきつけられて内側部分に電荷$-Q$が外側部分に$+Q$の電荷が分布します.
そこで,上図の①,②,③,④の部分における電場を求めてきましょう.
以下,球心からの距離を$x$としましょう.
①について$(0\leqq x\leqq r)$
①内部には電荷がありません.
また,①が囲む閉曲面の面積は球の表面積$4\pi x^2$なので,ガウスの法則より
$E_{1}=\dfrac{4\pi k_{0}\cdot 0}{4\pi x^2}=0$
つまり,導体球の内部の電場は0となります.
②について$(r\leqq x\leqq R_{1})$
②内部の電荷は$Q$です.
また,②が囲む閉曲面の面積は球の表面積$4\pi x^2$なので,ガウスの法則より
$E_{2}=\dfrac{4\pi k_{0}\cdot Q}{4\pi x^2}=k_{0}\dfrac{Q}{r^2}$
③について$(R_{1}\leqq x \leqq R_{2})$
③内部の電荷は$Q+(-Q)=0$です.
また,③が囲む閉曲面の面積は球の表面積$4\pi x^2$なので,ガウスの法則より
$E_{3}=\dfrac{4\pi k_{0}\cdot 0}{4\pi x^2}=0$
④について$(R_{2}\leqq x) $
④内部の電荷は$Q+(-Q)+Q=Q$です.
また,④が囲む閉曲面の面積は球の表面積$4\pi x^2$なので,ガウスの法則より
$E_{4}=\dfrac{4\pi k_{0}\cdot Q}{4\pi x^2}=k_{0}\dfrac{Q}{r^2}$
となります.
電場のグラフ
以上より,電場の大きさと導体球の中心からの関係のグラフは次のようになります.
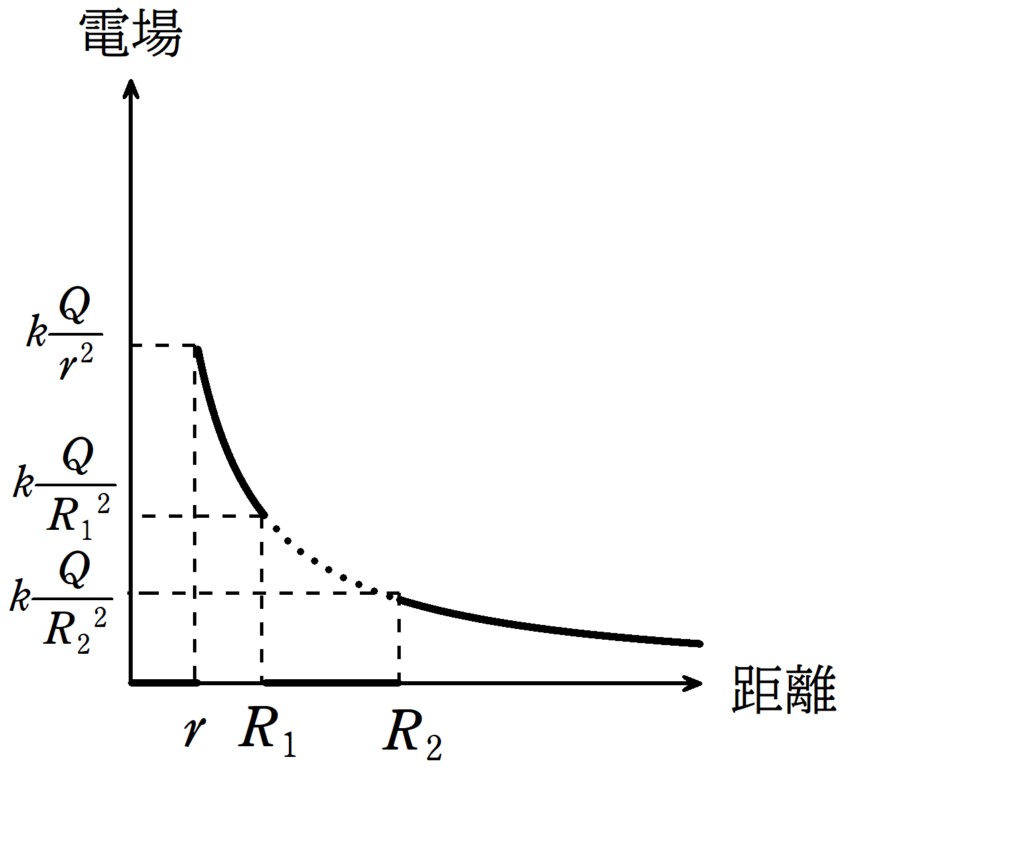
この電場のグラフによると,$0\leqq x\leqq r$と$R_{1}\leqq x \leqq R_{2}$の範囲では電場が0で静電気力がかからないことがわかります.
ちなみに点線部分は中空導体球がない場合です.
点線部分以外のところは中空導体球があってもなくても同じです.
正しい電位のグラフはどれか
電位の計算の仕方
電位の計算の仕方は重力のよる位置エネルギーと同じです.
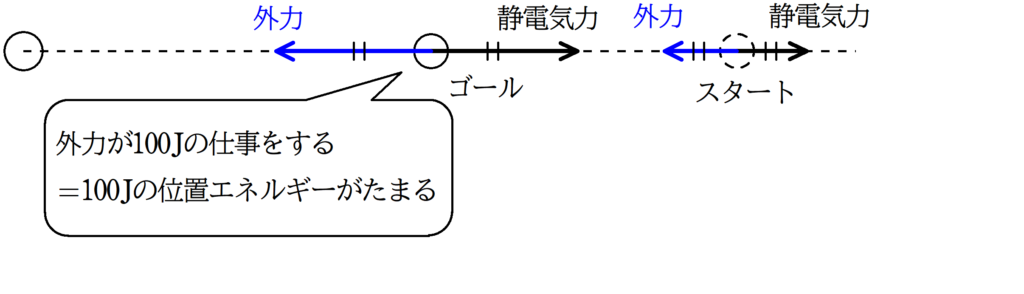
$1\rm{C}$の電荷に外力を加えてゆっくりと動かしたときに,外力が仕事をした分だけ電位がたまると考えます.
もし,外力を加える必要がない場合は電位はたまりません.
解答
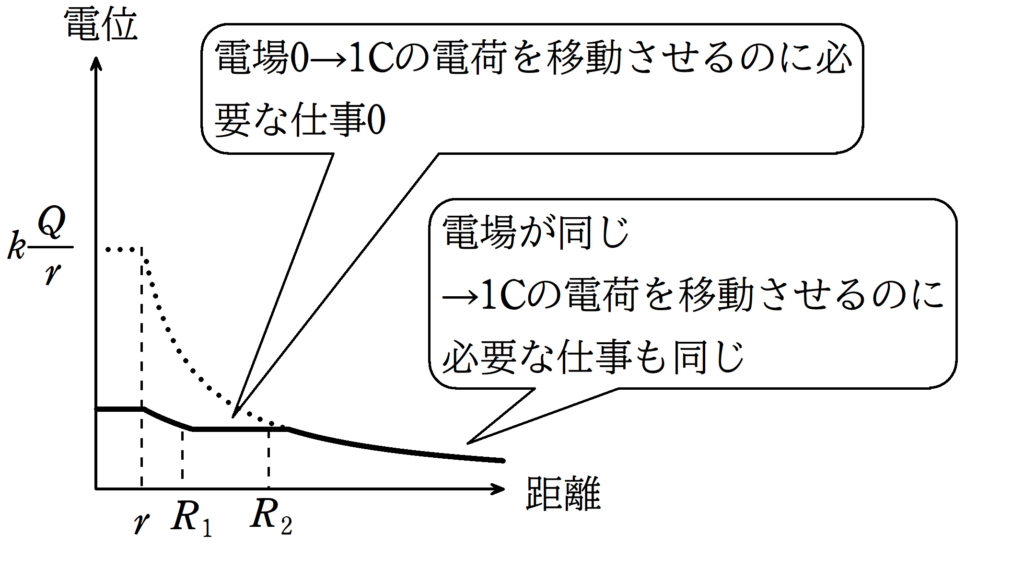
さて,位置エネルギーの基準点は無限遠です.
ここを$0\rm{V}$として$1\rm{C}$の電荷を動かしていきます.
$R_{2}\leqq x$では中空導体球があってもなくても電場は同じなので,電荷にはたらく静電気力も同じで,したがって外力も同じとなります.
つまり,外力がする仕事は中空導体球があってもなくても同じになるので$R_{2}\leqq x$では電位のグラフは点線部分と重なります.
そして,$R_{1}\leqq x \leqq R_{2}$では電場が0なので,静電気力もはたらきません.
したがって,$1\rm{C}$の電荷をゆっくりと動かすには外力を加えてはいけません.
外力がする仕事は0です.つまり,電位は変化しません.
その後,$r\leqq x\leqq R_{1}$では再び電場があるので,静電気力がはたらき,外力を必要とします.
したがって,外力が仕事をした分だけ電位が増えます.
最後に$0\leqq x\leqq r$では電場が0なので,静電気力も0.外力が仕事をしないので,電位は変化しません.

ということで,答えは③です.
ついつい①や④にしてしまいそうな気がしますね.
でも今,電位の基準点は無限遠なんです.
無限遠から$1\rm{C}$の電荷を動かしたときに外力が仕事をした分だけ電位が変化します.(なんとなく球の中心を基準にしないでくださいね)
そのとき,外力が仕事をしなかったら電位は変化しません.
なんか,受験勉強みたいですね.努力したら伸びるけど勉強しなかったら伸びない・・・.




コメント