
今回はばねつきピストンの問題です.次のことを要チェック!
- 熱力学の問題で立てて欲しい3つの式
- 気体がする仕事の計算の3つの方法
では,さっそく問題を解きましょう.
ちなみに,解答は一番最後に書いてあります.
図のように,水平な床の上に断熱容器が置かれている.断熱容器内部は断面積$S$のピストンによって2つの空間に分けられている.ピストンの上側は真空で,下側には単原子分子理想気体が封入されている.また,ピストンの質量は$m$であり,ピストンにはばね定数$k$のばねが取り付けられている.また,断熱容器の内側部分の底には,ヒーターが取り付けられており,気体に熱を与えることができるようになっている.はじめ,ばねは自然長にあったものとして,この状態を状態Aとする.
ただし,重力加速度の大きさを$g$として,ピストンはなめらかに動けるようになっているものとする.
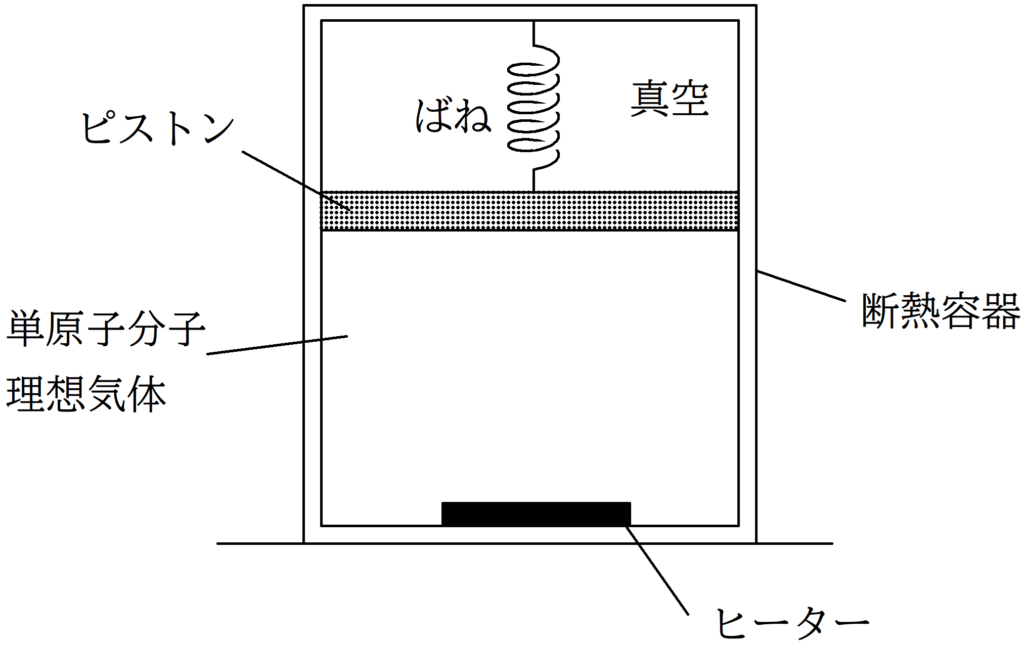
(1) 状態Aにおける,単原子分子理想気体の圧力$p_{\rm{A}}$を表す式として正しいものを次の中から選べ.
$① p_{\rm{A}}=mg$ $② p_{\rm{A}}=mgS$ $③ p_{\rm{A}}=\dfrac{mg}{S}$ $④ p_{\rm{A}}=\dfrac{mS}{g}$
(2) ヒーターを稼働させて気体をゆっくりと加熱したところ,ピストンはゆっくりと上昇し,自然長より$H$だけ縮んだところでヒーターを止めた.このときの状態を状態Bとする.状態Aから状態Bまでに気体がした仕事を$W_{1}$,弾性力による位置エネルギーの変化を$\Delta U_{1}$,ピストンの重力による位置エネルギーの変化$\Delta U_{2}$とするとき成り立つ関係式として,正しいものを次の中から選べ.
$① W_{1}+\Delta U_{1}+\Delta U_{2}=0$
$② W_{1}-\Delta U_{1}+\Delta U_{2}=0$
$③ W_{1}+\Delta U_{1}-\Delta U_{2}=0$
$④ W_{1}-\Delta U_{1}-\Delta U_{2}=0$
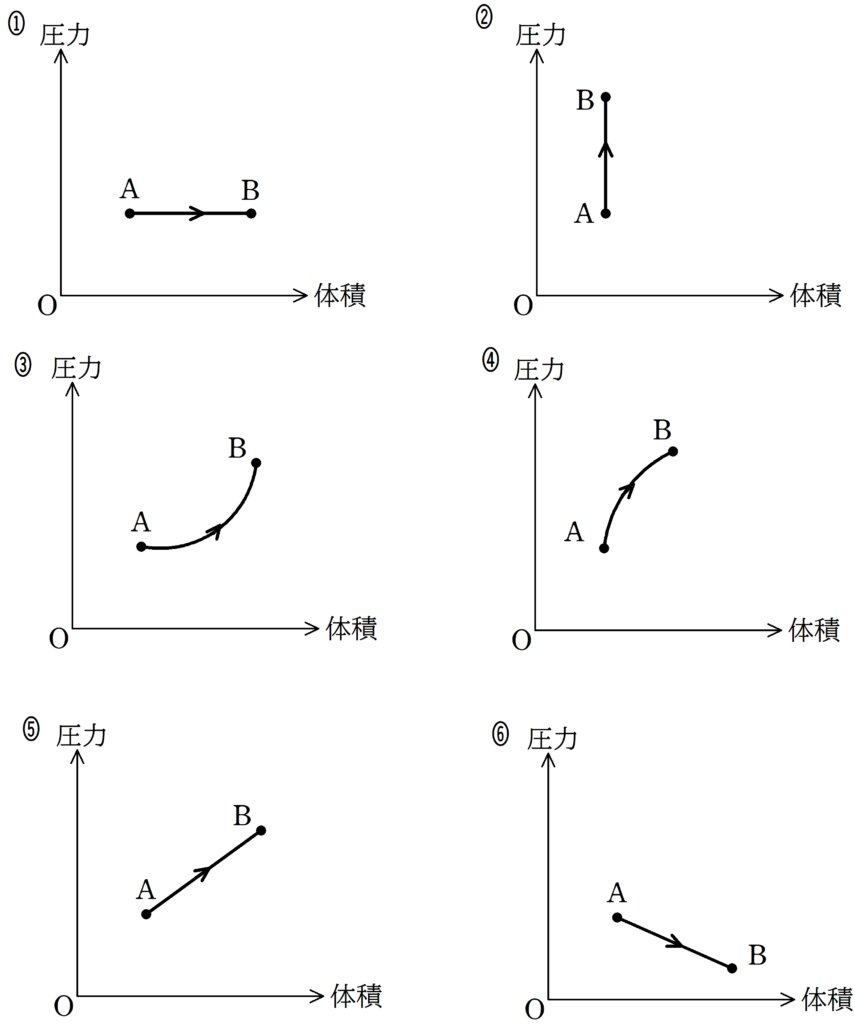
(3) 状態Aから状態Bまでの単原子分子理想気体の圧力と体積の変化のグラフとして最も適当なものを次の中から選べ.
熱力学の問題で立てて欲しい3つの式

熱力学の問題と言ったら次の3つの式を立てましょう!
- 可動部分のつり合いの式 → 力の情報が出てくる
- 理想気体の状態方程式(ボイルシャルルの法則)
- 熱力学第一法則 → エネルギーの情報が出てくる

何の式を立てればいいかわからなくなったら上の3つの式のどれを立てればいいかを考えましょう.
1.可動部分のつり合いの式
熱力学の問題のほとんどは”ゆっくり”と変化する,準静的変化です.つまり,可動部はつり合いを保ちながら動くとみなすことができます.
なので,1.可動部分のつり合いの式を立てることができます.
この式を立てることで,圧力や外部の力,質量や密度のような力に関係する物理量を求めることができます.また,どのような状態変化をするのかを考えるときもこの式を立てるとよいでしょう.
2.理想気体の状態方程式(ボイルシャルルの法則)
気体の圧力を$p$,体積を$V$,物質量を$n$,気体定数を$R$,絶対温度を$T$とするときに
$pV=nRT$
の関係を理想気体の状態方程式といいます.圧力,体積,絶対温度の関係式なので,これらを聞かれたら立てるとよいです.
また,$nR=一定$のとき
$\dfrac{pV}{T}=一定$
となり,これをボイル・シャルルの法則といいます.
3.熱力学第1法則
内部エネルギーの変化を$\Delta U$,気体が吸収する熱量を$Q$,気体がした仕事を$W$とすると,次の関係が成り立ちます.
$Q=\Delta U+W$
内部エネルギーの変化,熱量,仕事について聞かれたらこの式を立てるとよいでしょう.
(1)の解答
気体の圧力について聞かれているので,真っ先に立てる式は
1.可動部分のつり合いの式
です.
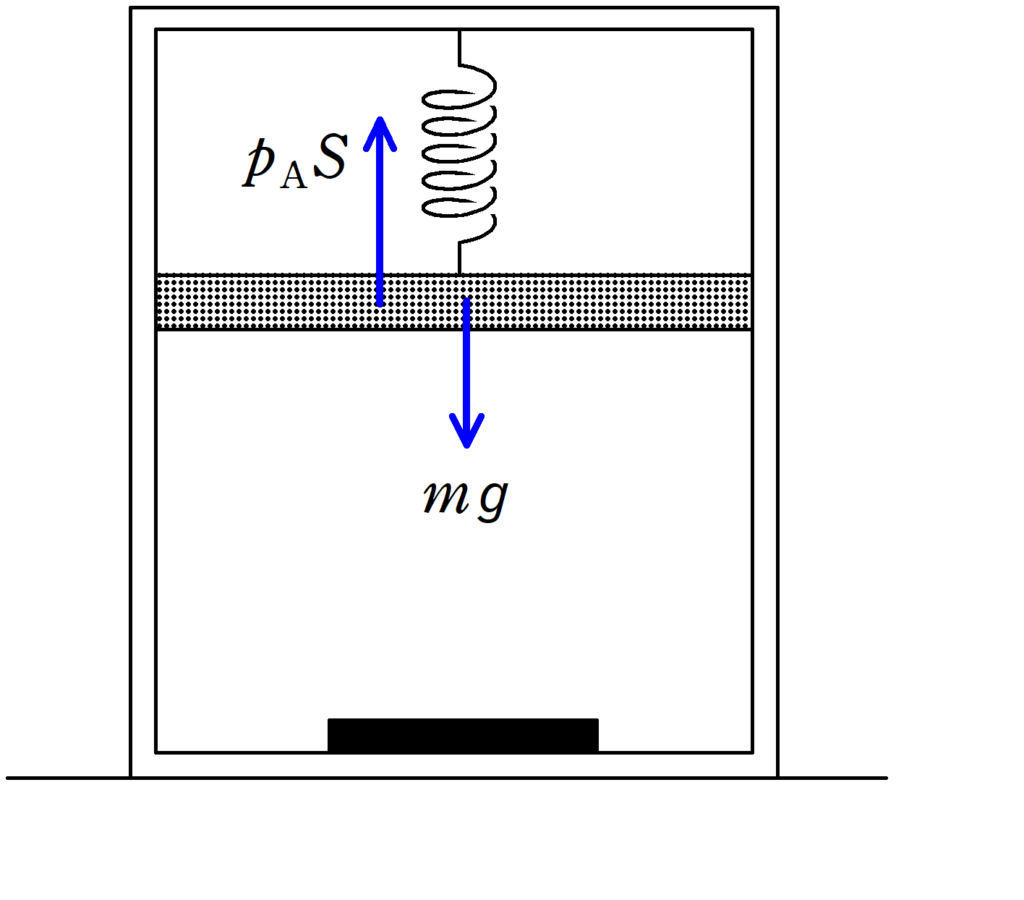
今回の可動部分というのはピストンのことです.”ある程度自由に動く”ところを対象として考えましょう.
ピストンにばねがついているものの,自然長なので,弾性力ははたらきません.
状態Aにおける圧力を$p_{\rm{A}}$とすると,気体がピストンを押す力は上向きに$p_{\rm{A}}S$となります.
また,ピストンにかかる重力が$mg$なので,つり合いの式は
$p_{\rm{A}}S=mg$ $\therefore p_{\rm{A}}=\dfrac{mg}{S}$
したがって,解答は$③$です.

これくらいだったら,単位を考えるだけでもわかっちゃうね!
気体がする仕事を求める3つの方法

“気体がする仕事”と聞かれたら次の3つを思い浮かべるようにしましょう!
- $pV$グラフの面積を求める.
- 熱力学第1法則から求める.
- 可動部分のエネルギー保存から求める.
1.$pV$グラフの面積を求める.
$pV$図に関してはこちらに詳しく書いてあるので参考にしてください.
2.熱力学第1法則から求める.
こちらは先ほど紹介した,熱力学の問題で立てる3つの式と同じです.
3.可動部分のエネルギー保存から求める.
こちらは意外と抜けがちです.例えば,今回であれば,ピストンに関するエネルギー保存を考えます.
熱力学というより,力学の問題としてとらえると一気に求めたいものにたどり着くことができます.
(2)の解答+気体がする仕事の計算
ピストンに着目してエネルギー保存則を立てます.ピストンには保存力である重力と弾性力,そして,非保存力である単原子分子理想気体がピストンに与える力がはたらきます.
また,運動エネルギーの変化は最初と最後が静止してるため0です.
力学的エネルギーの変化=非保存力がした仕事
の式を立てると
$\Delta U_{1}+\Delta U_{2}=W_{1}$ $\dots (\clubsuit)$
したがって
$W_{1}-\Delta U_{1}-\Delta U_{2}=0$
より,答えは$④$です.
では,ついでに気体がする仕事$W_{1}$を計算してみましょう.
弾性力による位置エネルギーの変化$\Delta U_{1}$は
$\Delta U_{1}=\dfrac{1}{2}kH^{2}-\dfrac{1}{2}k\cdot 0^{2}=\dfrac{1}{2}kH^{2}$
重力による位置エネルギーの変化$\Delta U_{2}$は状態Aの位置を基準として
$\Delta U_{2}=mgH-mg\cdot 0=mgH$
$(\clubsuit)$より
$W_{1}=\dfrac{1}{2}kH^{2}+mgH$ $\dots (\ast)$
(3)の解答+気体がする仕事の計算
$pV$グラフは,状態変化の途中の可動部分のつり合いの式を立てればよいです.
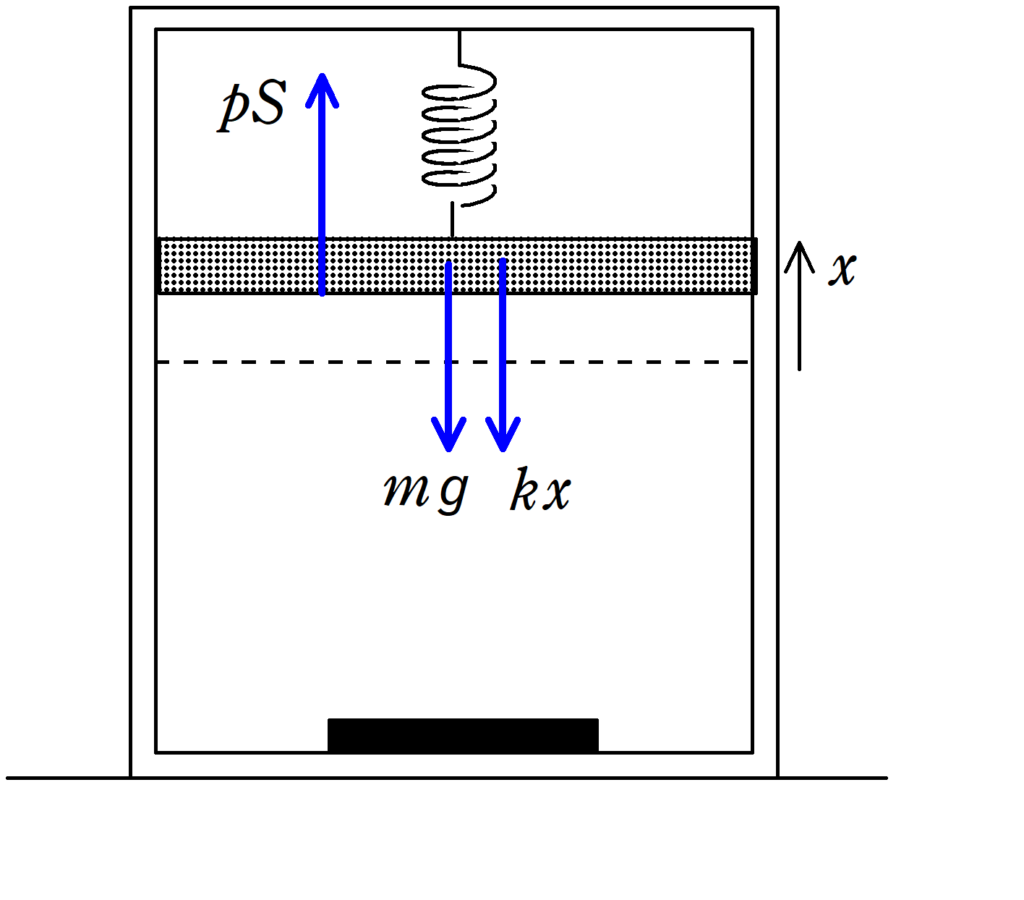
上図はばねが自然長より$x$縮んだときの図です.
ピストンにはたらく力は鉛直下向きに重力$mg$と,同じく下向きに弾性力$kx$,そして,気体の圧力を$p$とすれば,上向きに$pS$がはたらきます.
つり合いの式より
$pS=kx+mg$ $\therefore p=\dfrac{kx}{S}+\dfrac{mg}{S}$ $\dots (2\ast)$
さて,状態Aでの容器内部の底からピストンまでの距離を$L$とすれば,ばねが$x$だけ縮んだときの気体の体積$V$は
$V=S(L+x)$
です.すなわち
$x=\dfrac{V}{S}-L$ $\dots (3\ast)$
$(3\ast)$を$(2\ast)$に代入すると
$p=\dfrac{k}{S}(\dfrac{V}{S}-L)+\dfrac{mg}{S}=\dfrac{k}{S^2}V+\dfrac{mg-kL}{S}$
となります.ここで,$pV$グラフをかくので,$p$と$V$に注目すると
$p$$=\dfrac{k}{S^2}$$V$$+\dfrac{mg-kL}{S}$
これは,$y$$=a$$x$$+b$の形になっているので,$pV$グラフは直線になります.しかも,$V$の係数である$\dfrac{k}{S^2}$は正の数なので,傾きが正の直線ですね.
したがって,答えは$⑤$です.
さて,$pV$グラフから気体がした仕事を計算してみましょう.果たして可動部分のエネルギー保存から得た$(\ast)$と同じ式になるのでしょうか.
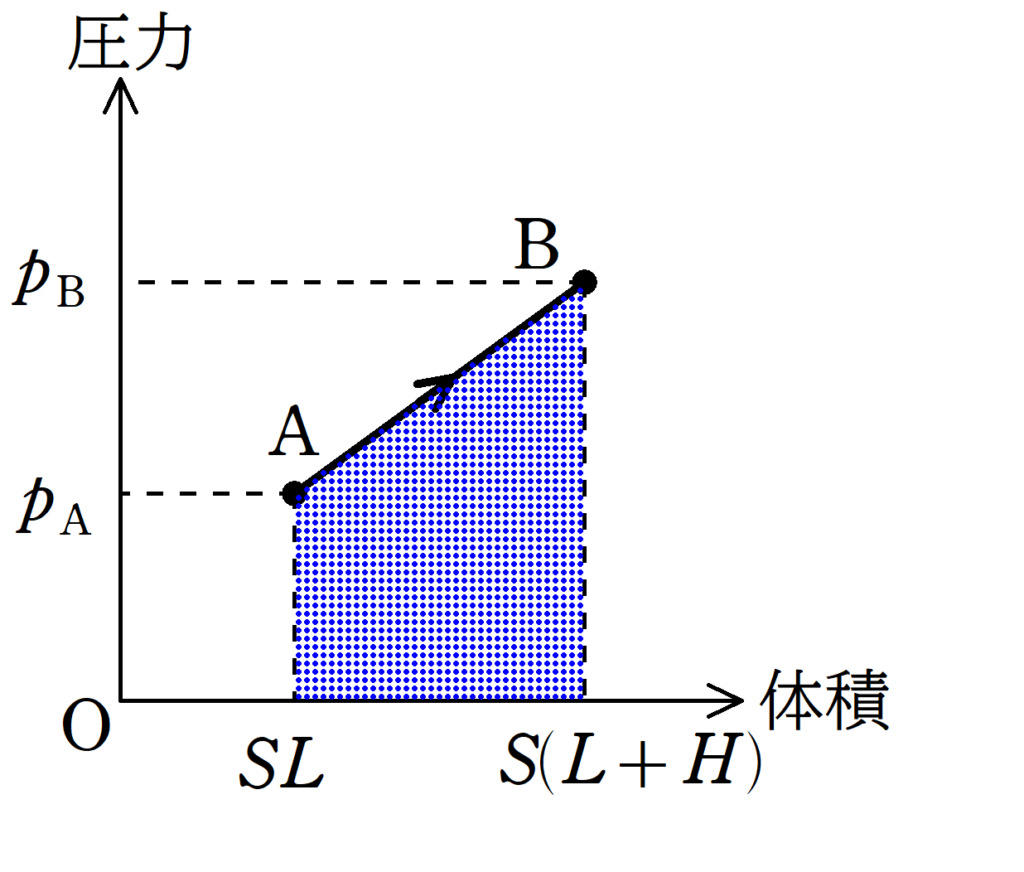
まず,上図の$p_{\rm{A}}$は(1)で考えたように,$p_{\rm{A}}=\dfrac{mg}{S}$です.
また,$p_{\rm{B}}$は,状態Bでのつり合いの式を立てると,重力$mg$と弾性力$kH$と気体がピストンをおす力$p_{\rm{B}}S$の関係は
$p_{\rm{B}}S=mg+kH$ $\therefore p_{\rm{B}}=\dfrac{mg+kH}{S}$
したがって,上図の台形の面積が気体がした仕事$W_{1}$なので
$\eqalign{W_{1}&=\dfrac{1}{2}(p_{\rm{A}}+p_{\rm{B}})\cdot SH\\&=\dfrac{1}{2}(\dfrac{mg}{S}+\dfrac{mg+kH}{S})SH\\&=\dfrac{1}{2}kH^{2}+mgH} $

たしかに一緒になったね!
2次試験対策のためにも2通りの解き方で計算できるようにしておきましょう!
解答
(1) ③ (2) ④ (3) ⑤





コメント
[…] […]