※ ”作図”という言葉より,”描き方”の方が適切でしょう.

自由端反射と固定端反射の描く問題がむずかしい..
描き方の手順をみればできるけど,すぐ忘れてしまうし,自由端と固定端の区別がいまいちつかない.

そうですね.今回は自由端反射と固定端反射の描き方についての話をしましょう.
この記事は次の方におすすめです.
- 自由端反射と固定端反射の図を描く際に,意味を確認しながら解きたい人
- いざ,問題が出たときに思い出すステップを整理したい人

意味を確認しながらなら忘れにくいね!
自由端反射と固定端反射の描き方まとめ

はじめに,理屈抜きで自由端反射と固定端反射の描き方をまとめておきましょう.
・自由端反射
- 反射面がなかったものとして,仮想入射波を描く.
- 仮想入射波を反射面について折り返す.
・固定端反射
- 反射面がなかったものとして,仮想入射波を描く.
- 仮想入射波を横軸について折り返す.
- 2で折り返した波を反射面について折り返す.
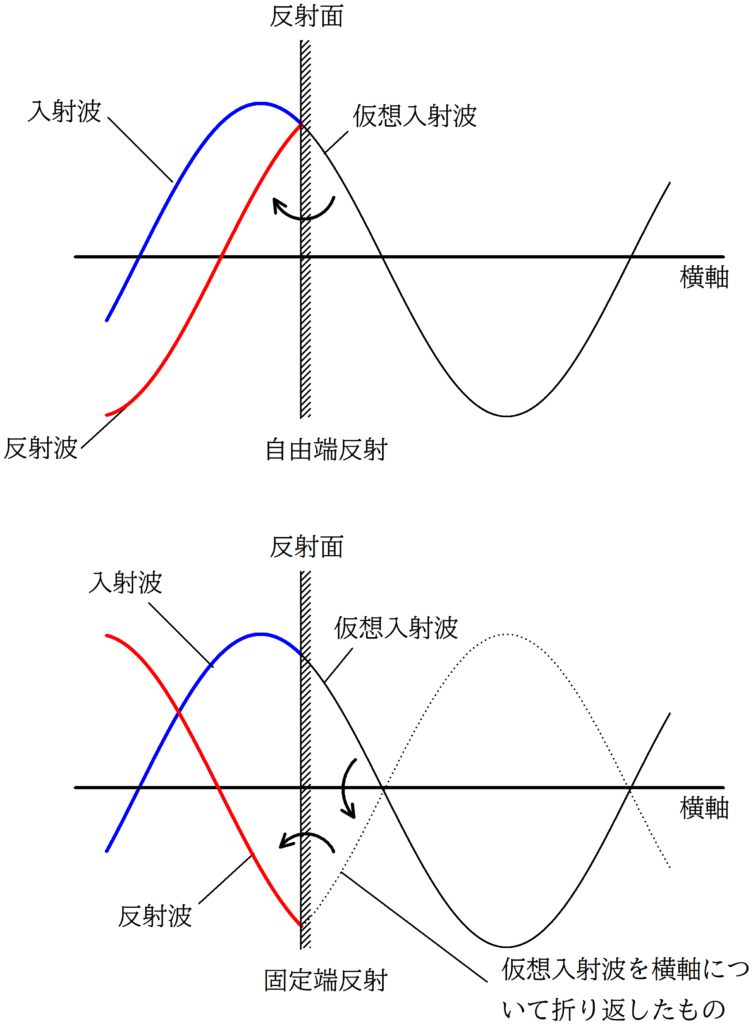
固定端反射・自由端反射とは
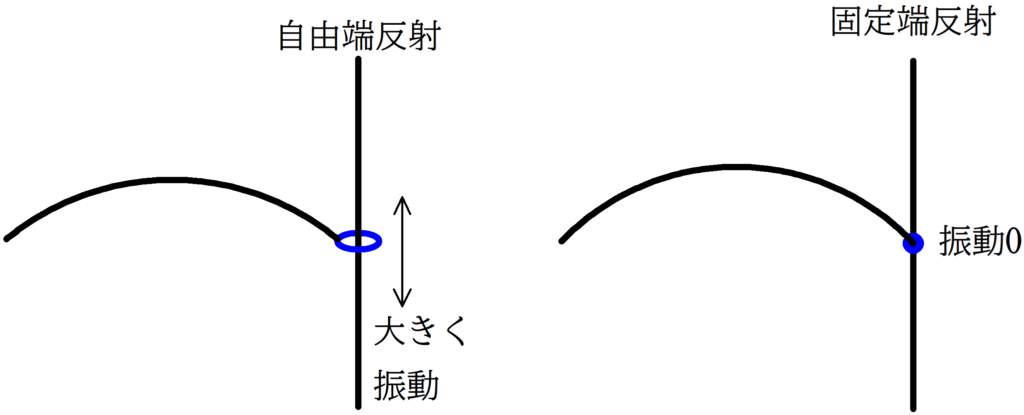
自由端反射では反射する場所で大きく振動し,固定端反射では反射する場所で振動が0になります.
これは次のように考えることができます.
・自由端反射
入射波と反射波の反射面での媒質の振動の位相(タイミング)が同じだから大きく振動する.
・固定端反射
入射波と反射波の反射面での媒質の振動の位相(タイミング)が$\pi$ずれているから振動しない.
・自由端反射では入射波と反射波の位相(タイミング)のずれはない.
・固定端反射では入射波と反射波の位相(タイミング)は$\pi$ずれる.
位相が$\pi$ずれるとは?

そもそも位相が$\pi$ずれるってどういう意味?

下の単位円をみてください.
位相が$\pi$ずれると単位円上の$x$座標も$y$座標も真逆になっていることがわかります.
媒質の振動が真逆→位相(タイミング)が$\pi$ずれている
と言えます.
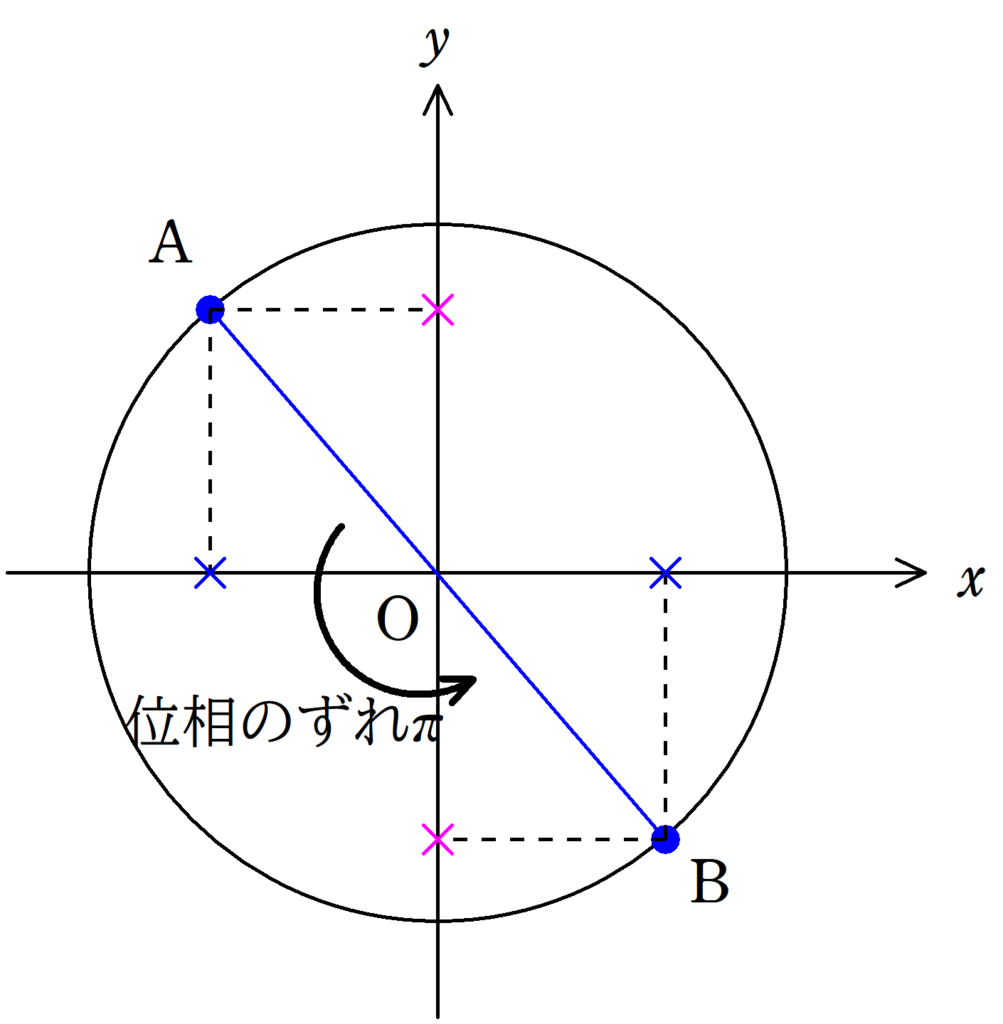

これは$\sin(\theta +\pi)=-\sin \theta$の公式を使えば,計算でも確認できるよね.
$\sin(\theta +\phi +\pi)=-\sin(\theta +\phi)$

そうですね.
そして,一般的に,$y=f(x)$と$y=-f(x)$は$x$軸対称の関係にあります.
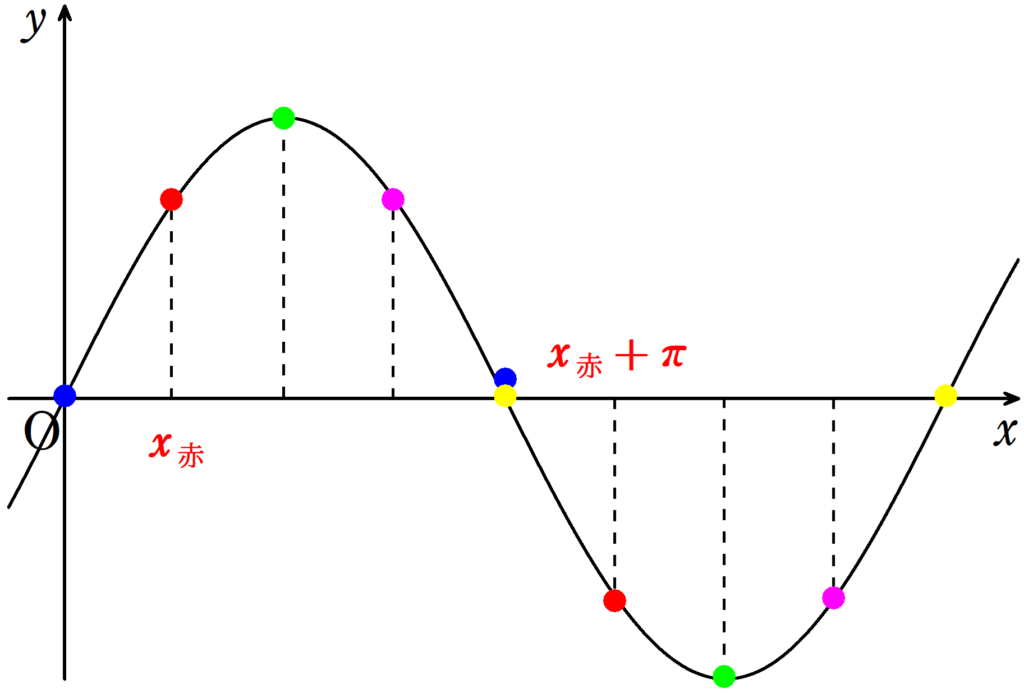

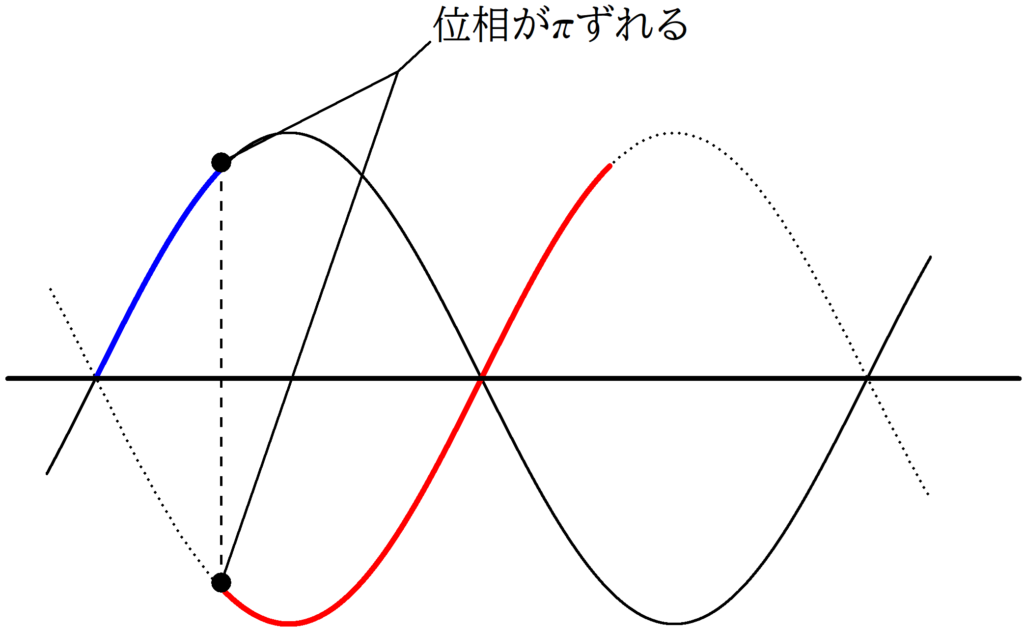
上の図の同じ色どうしの点はそれぞれ位相の差が$\pi$となっています.
たとえば,左側の赤い点の$x$座標を$x_{赤}$として,右側の赤の点の$x$座標を$x_{赤}+\pi$としましょう.
$x_{赤}$の点で急に位相が$\pi$ずれたらどのような点にうつるのでしょうか?
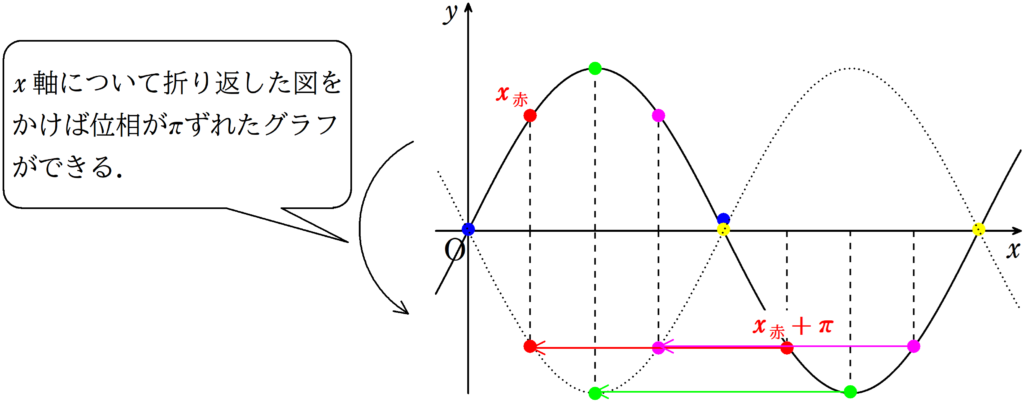

位相が$\pi$ずれた点をかくには,次のようにすればよいでしょう.
$x_{赤}$にある点を$x$軸について折り返す.
すると,位相が$\pi$ずれた点をかくことができます.

さっき,計算したように,位相が$\pi$ずれるということは
$\sin(x_{赤} +\pi)=-\sin(x_{赤})$
の関係があって,
$y=f(x)$と$y=-f(x)$は$x$軸対称の関係
にあるからからだよね.

そういうことです.
もちろん,青や緑やピンクの点,それぞれについても同じことが言えます.
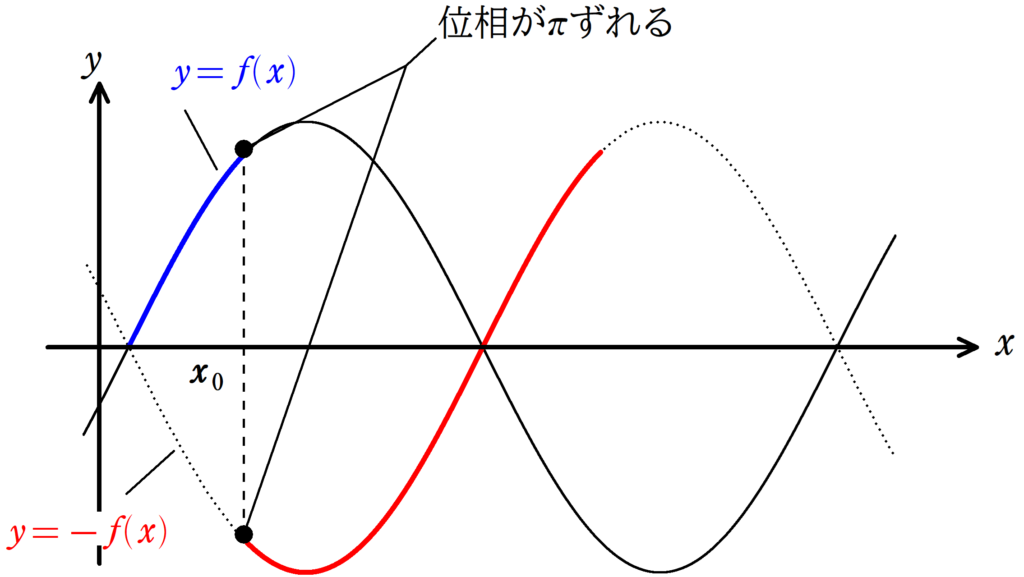
正弦関数$y=f(x)$において,$x=x_{0}$から位相が$\pi$ずれたグラフは次の手順で描く.
- $y=f(x)$のグラフを$x$軸について折り返したグラフ$y=-f(x)$のグラフを描く.
- $x=x_{0}$の点を境に$y=-f(x)$のグラフにうつして描く.
自由端反射の反射波の描き方

自由端反射では位相のずれはないから,そのままはねかえるんだね!
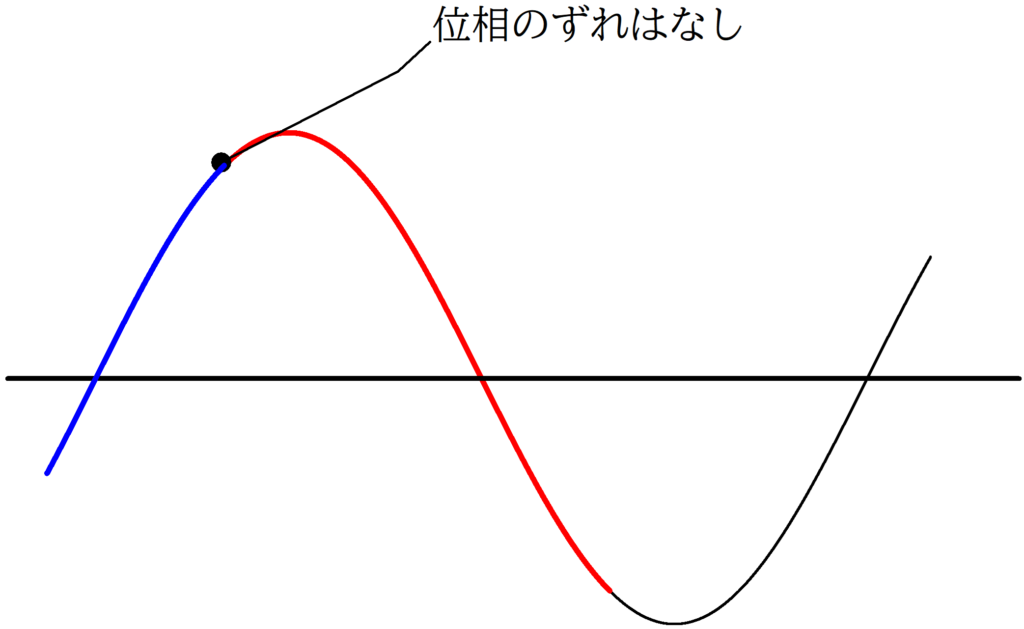

そういうことです.
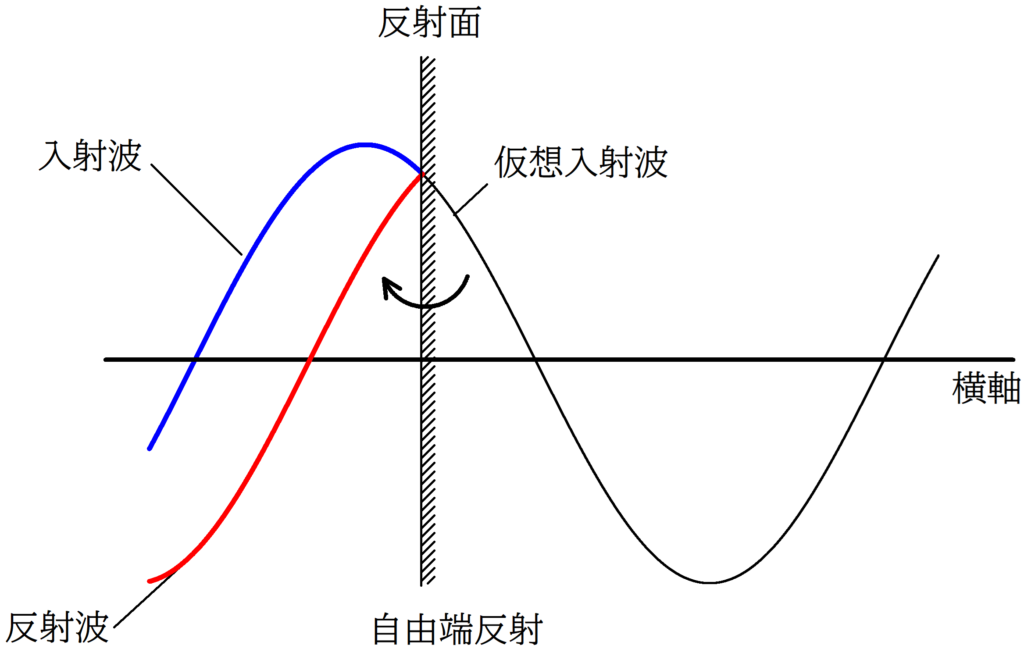
たとえば,上図の黒点のところで位相のずれがなかったら青部分と赤部分をつなげて描けばよいでしょう.
そして,下図のように,自由端反射をすれば,そのまま赤い部分が左側にいくだけです.
つまり,反射面について折り返せばいいんです.
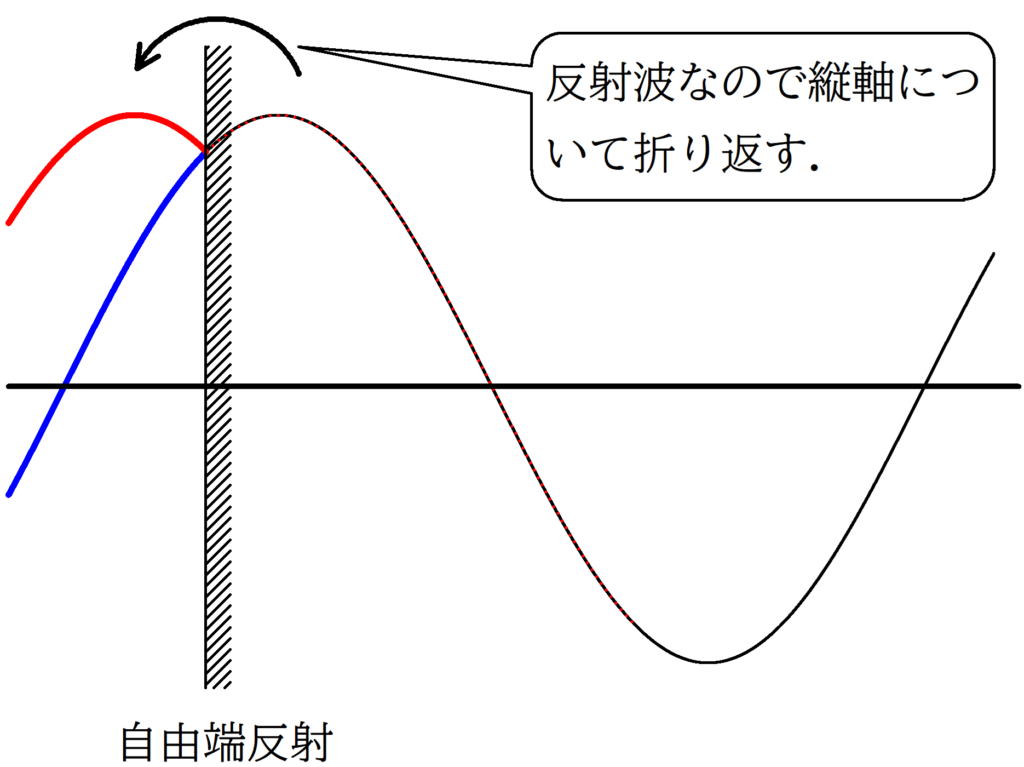
・自由端反射
- 反射面がなかったものとして,仮想入射波を描く.
- 仮想入射波を反射面について折り返す.
※ 自由端反射では位相がずれないので,そのまま折り返せばよい.
固定端反射の反射波の描き方

固定端反射をすると,位相が$\pi$ずれます.
位相が$\pi$ずれる点の描き方は
- $y=f(x)$のグラフを$x$軸について折り返したグラフ$y=-f(x)$のグラフを描く.
- $x=x_{0}$の点を境に$y=-f(x)$のグラフにうつして描く.
でした.
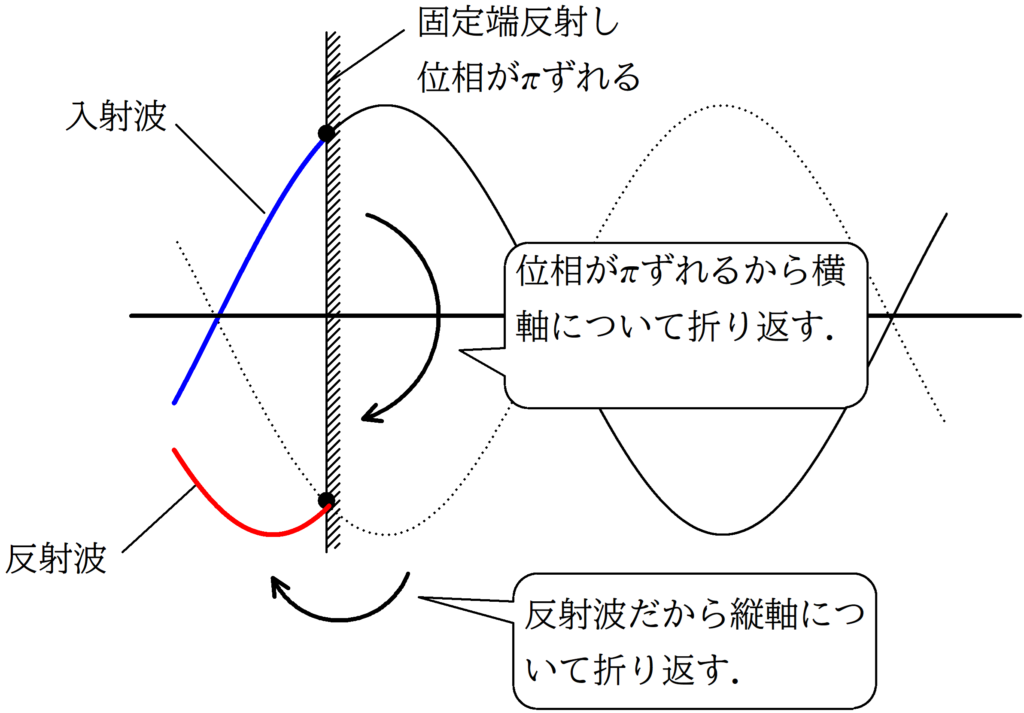

そして,位相が$\pi$ずれたグラフが反射されて伝わっていくんだね!
- 位相が$\pi$ずれるから横軸について折りかえす.
- 反射波を考えるから縦軸(反射面)について折りかえす.
意味がわかれば忘れにくそう!
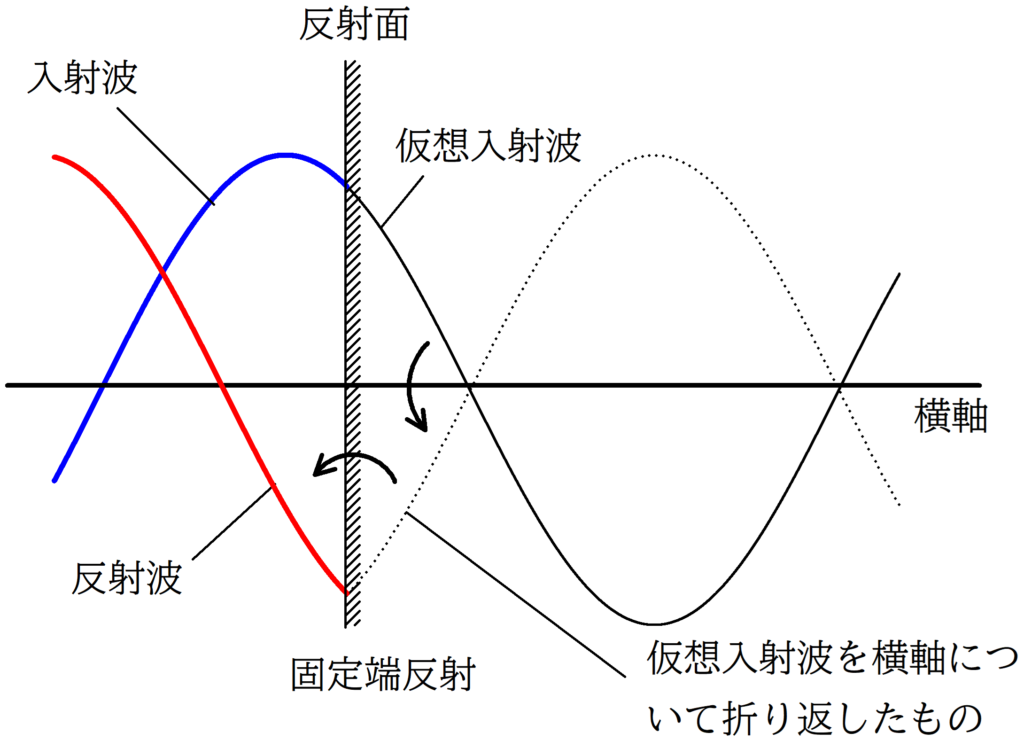
・固定端反射
- 反射面がなかったものとして,仮想入射波を描く.
- 仮想入射波を横軸について折り返す.
- 2で折り返した波を反射面について折り返す.
※固定端反射では位相が$\pi$ずれるから,横軸で折り返す.反射波だから縦軸に折り返す.
演習問題

では,演習問題を解いて確認してみよう.
次の(1),(2)において,入射波が描かれている.この時刻における反射波のグラフを,自由端反射の場合と固定端反射の場合,それぞれについて描け.
(1)
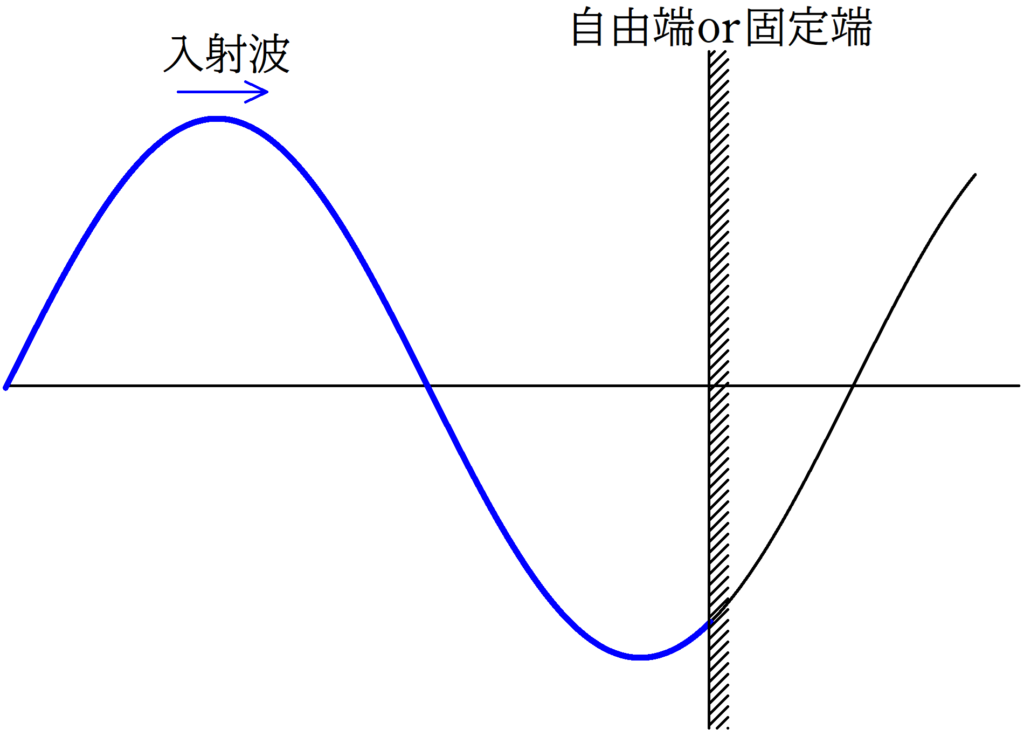
(2)
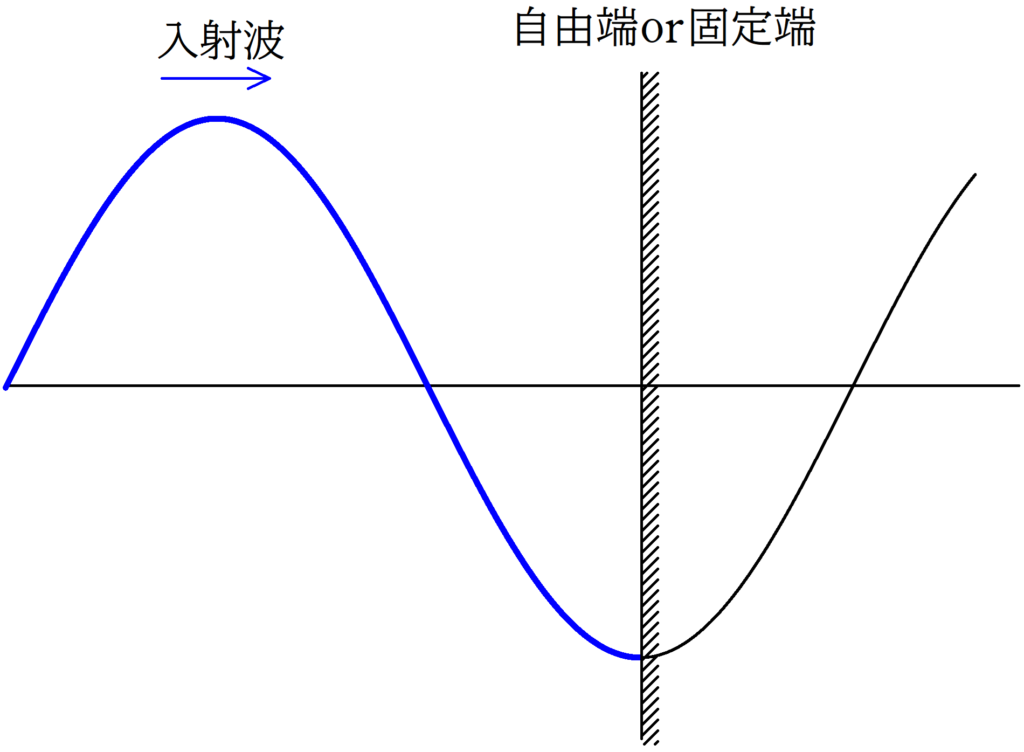
演習問題解答
(1)解答
★自由端反射の場合
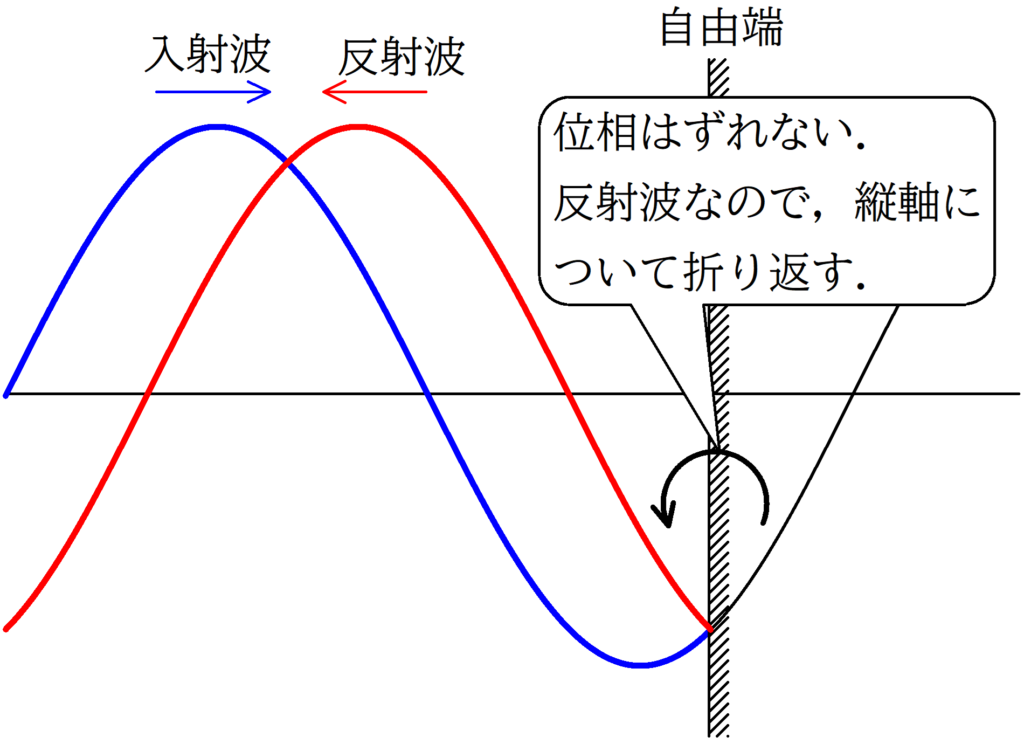
★固定端反射の場合
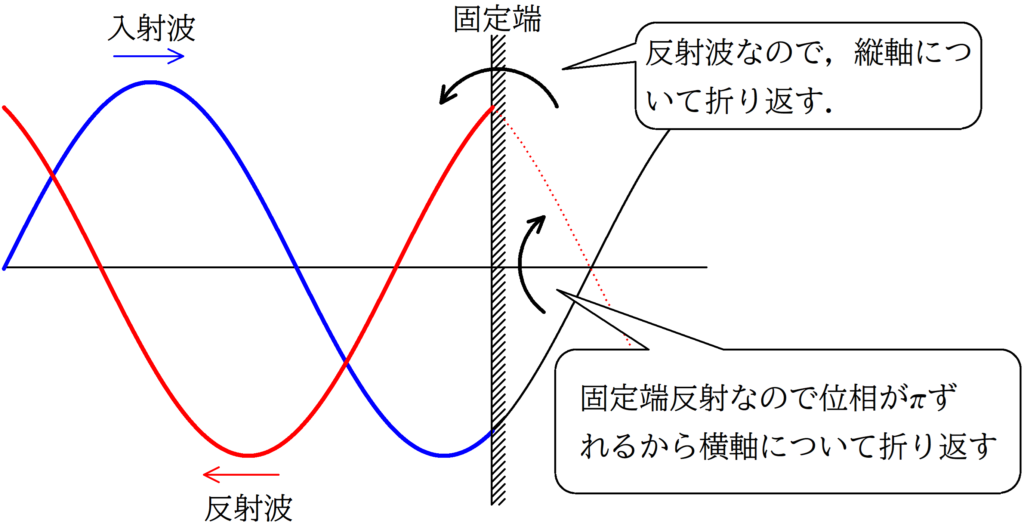
(2)の解答
★自由端反射の場合
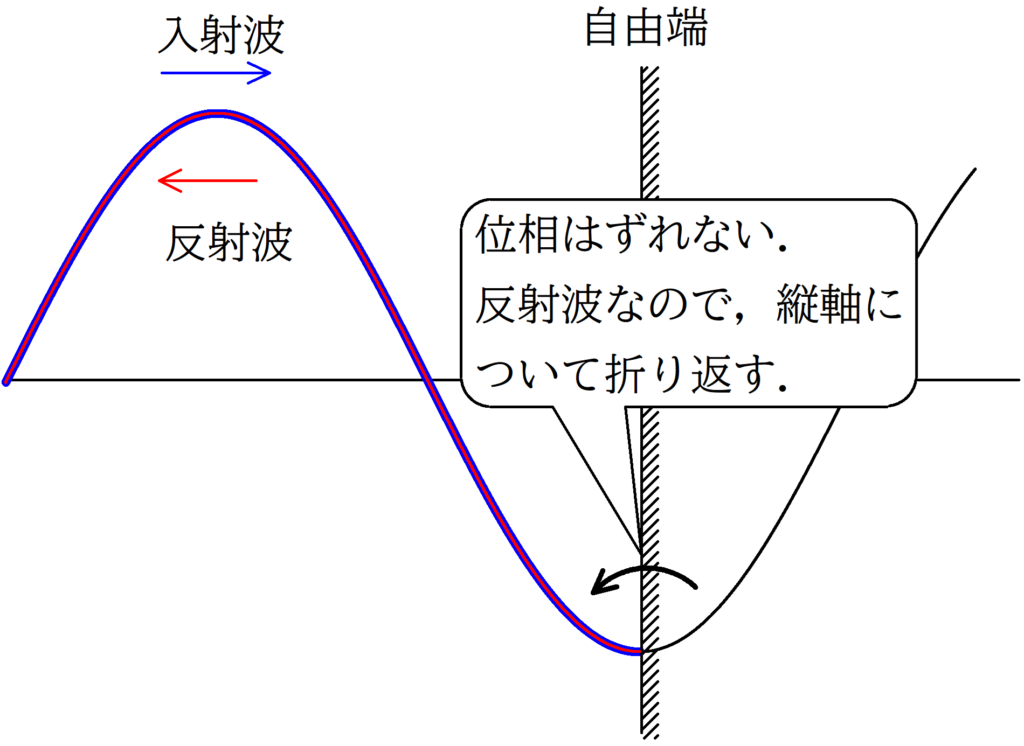
★固定端反射の場合
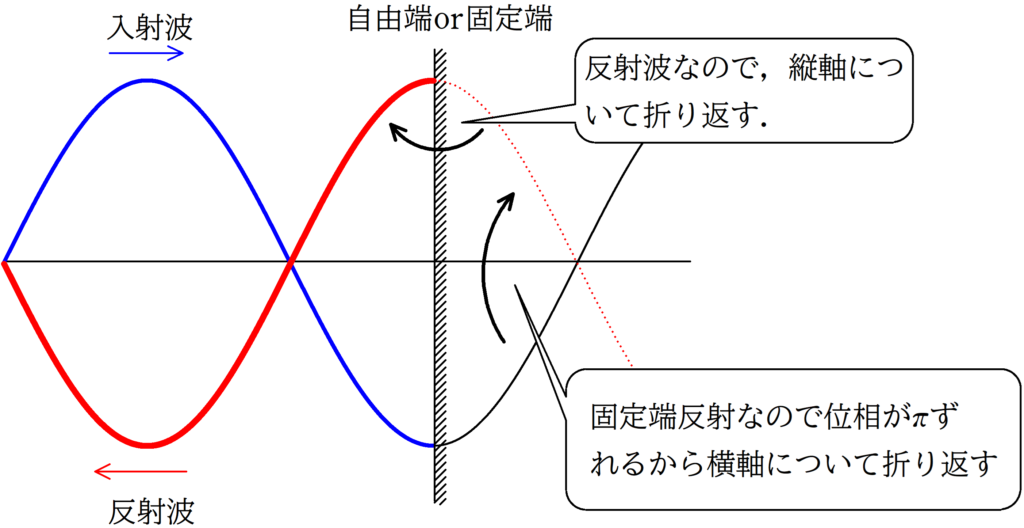

最後のまとめです!
グラフを折り返す理由のまとめ
- 横軸について折り返す理由→位相が$\pi$ずれるから
- 縦軸について折り返す理由→反射波は波の向きが真反対になるから

折り返す理由を覚えておくと,忘れにくいと思います!




コメント
[…] […]
[…] […]
[…] 自由端反射と固定端反射の描き方[作図] […]