
物体が半円筒に接しながら円運動をして,最高点に達する条件について話です.
問題文には,「半円筒に接しながら,」の部分は書かれていないことも多いです.
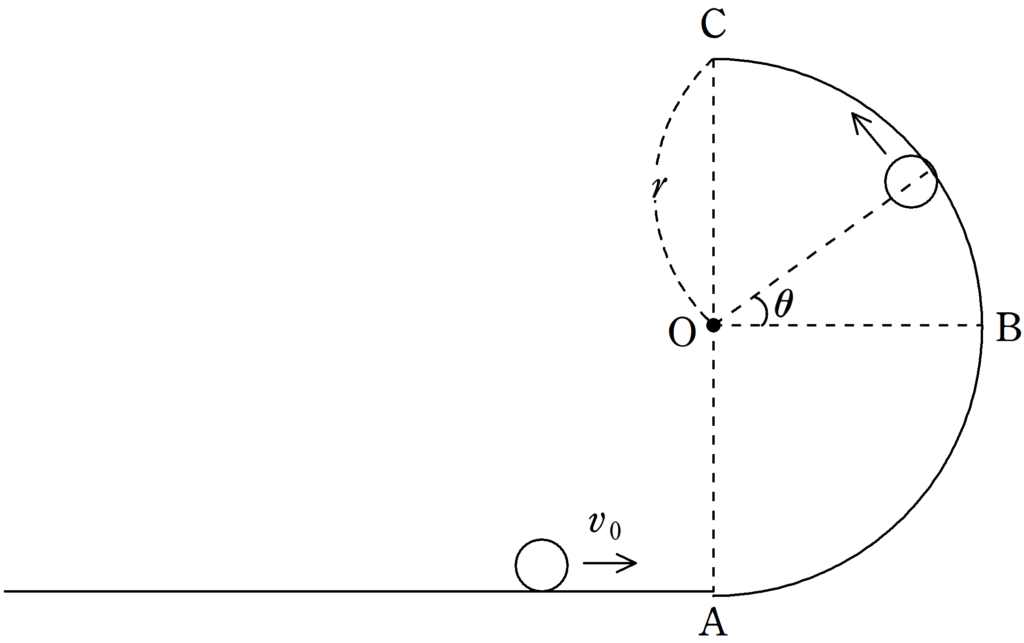

上図のように,水平面で初速度を与えて,鉛直面内を円運動します.
A→B→Cと最高点Cに達する条件は,次のようになります.
最高点Cでの垂直抗力$>0$

よくある間違いとしては,
Aでの運動エネルギー$>$Cでの重力による位置エネルギー
としてしまうことです.
なぜ,これではだめなのかも話していきます.

では,まず途中経過を考えましょう.
A→Bでは円筒面から離れることはないのでよいでしょう.
B→Cの間のPにいるときを考えます.
$\angle \rm POB=\theta$としましょう.
今回は次の2つの式を立てます.
- 力学的エネルギー保存則
- Pにおける向心方向の運動方程式
★ 力学的エネルギー保存則
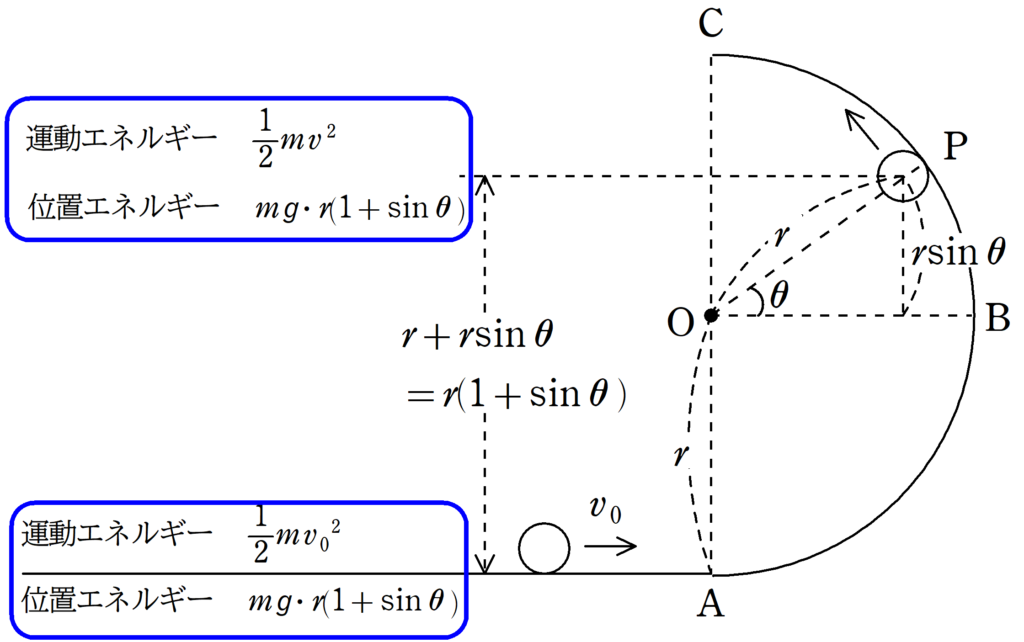
Aの位置を重力の位置エネルギーの基準点とします.また,円筒の半径を$r$としましょう.
AとPとの高さの差は
$r+r\sin\theta=r(1+\sin\theta)$
Aにおける速さを$v_{0}$,Pにおける速さを$v$とすると,力学的エネルギー保存則より
$\dfrac{1}{2}mv_{0}^{2}+0=\dfrac{1}{2}mv^{2}+mgr(1+\sin\theta)$
これを$v^{2}$について解くと
$v^{2}=v_{0}^{2}-2gr(1+\sin\theta)$ $\dots (\ast)$
★ 向心方向の運動方程式
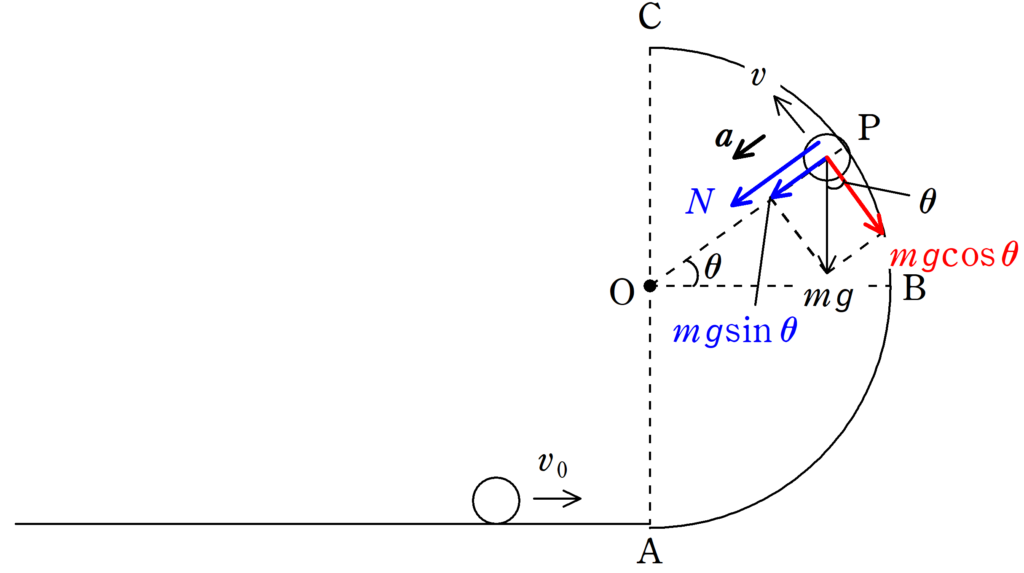
PにおけるO方向の加速度は$\dfrac{v^{2}}{r}$です.
Oの方向には,円筒面からの垂直抗力(大きさを$N$とする)と重力を分解した成分$mg\sin\theta$があります.
したがって,PにおけるO方向の運動方程式は
$m\dfrac{v^{2}}{r}=N+mg\sin\theta$ $\dots (2\ast)$

$(\ast)$を$(2\ast)$に代入して,垂直抗力の大きさ$N$を$\theta$の関数として表してみましょう.
$(\ast)$を$(2\ast)$に代入して
$\eqalign{\dfrac{m}{r}\cdot \{v_{0}^{2}-2gr(1+\sin\theta)\}&=N+mg\sin\theta \cr m\dfrac{v_{0}^{2}}{r}-2mg(1+\sin\theta)&=N+mg\sin\theta \cr N=m\dfrac{v_{0}^{2}}{r}-(3+2\sin\theta)mg}$

$\sin\theta$は$0\leqq\theta\leqq\dfrac{\pi}{2}$の範囲では,$\theta$が大きくなると,$\sin\theta$も大きくなります.
上の式からわかるように,$\theta$が大きくなると,$N$がだんだんと小さくなっていきます.
$N$が0になると,その地点で円筒から離れます.
なので,BからCの各地点で$N>0$であればよいのですが,最高点に達する条件を考えるだけであれば,
最高点での$N>0$
だけでよいです.
理由は明白.$\theta$が大きい,つまり,上にいけば上にいくほど,$N$が小さくなっていくのがわかったので,最高点で$N>0$であれば,他の点でも$N>0$であることが保証されているからです.
つまり,最高点に達する条件は,$\theta =\dfrac{\pi}{2}$のとき,$N>0$つまり
$\eqalign{m\dfrac{v_{0}^{2}}{r}-(3+2\sin\dfrac{\pi}{2})mg&>0 \cr m\dfrac{v_{0}^{2}}{r}&>5mg \cr v_{0}&>\sqrt{5gr}}$

言い換えれば,$v_{0}>\sqrt{5gr}$を満たす$v_{0}$でなければ,途中で円筒を離れてしまうことになります.

では,Aでの運動エネルギー$>$Cでの位置エネルギーでは,なぜだめなのかを確かめましょう.
Cでの位置エネルギーは$mg\cdot 2r=2mgr$であるから
$\dfrac{1}{2}mv_{0}^{2}>2mgr$
$\therefore v_{0}>\sqrt{4gr}$

これでは,$v_{0}>\sqrt{5gr}$を満たしませんね...
今回は,離れずに最高点に達する条件を考えているんです.
円筒面が動かない場合,円筒面を離れず最高点に達する条件は
最高点での垂直抗力$>0$
である.この条件式をつくるのに,以下の2つの式を立てる.
- 力学的エネルギー保存則
- 向心方向の運動方程式




コメント
[…] [鉛直面内の円運動]最高点に達する条件 […]