圧力が一定である条件のもとで,気体の体積[$\rm m^{3}$]と温度[$\rm ^{\circ}C$]の関係を調べる実験を行った.
その結果について,気体の体積と温度の関係をグラフにしたところ,図1のようになった.図1のように,温度が$0 \rm ^{\circ}C$のときの気体の体積は$v_{0}$[$\rm m^{3}$]であった.
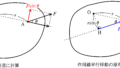
さらに,図1のグラフの直線を伸ばし,目盛りを読み取ると,横軸と交わる点が$-t_{0}[\rm ^{\circ}C]$であった.ただし,$t_{0}>0$である.(図2)
このことから,体積$v$[$\rm m^{3}$]と温度$t$[$\rm ^{\circ}C$]の関係式は次のようになる.
$v=v_{0}(1+\dfrac{t}{t_{0}})$ $\dots (\ast)$

問 体積$v$[$\rm m^{3}$]と温度$t$[$\rm ^{\circ}C$]について$(\ast)$が成り立つとき,$v$と$t$の関係として正しい記述を次の中から選べ.
① $v$と$t$は比例関係にある.
② $v$と$t$は反比例の関係にある.
③ $v$と$t^{2}$は比例関係にある.
④ $v$と$t+t_{0}$は比例関係にある.
⑤ $v$と$t+t_{0}$は反比例の関係にある.
⑥ $v$と$(t+t_{0})^{2}$は比例関係にある.

さて,答え合わせです!
$t_{0}$が何かを知っていれば,答えはすぐにわかるのですが,$(\ast)$の式を考察してみることにしましょう.
$v=v_{0}(1+\dfrac{t}{t_{0}})$ $\dots (\ast)$
について,$v_{0}$と$t_{0}$は定数で,$v$と$t$は変数です.
$(\ast)$を変形して
$v$$=\dfrac{v_{0}}{t_{0}}$$t$$+v_{0}$
の形にすると,$y$$=a$$x$$+b$の形から,$v$と$t$は比例関係にないことはすぐにわかると思います.
比例関係にあるときは,原点を通るときで,$y$$=a$$x$の形になるときです.
そして,式の形から反比例や2乗に比例でもないことはすぐにわかります.
そこで,次のように考えます.
$v=v_{0}(1+\dfrac{t}{t_{0}})$ $\dots (\ast)$
を
$v$$=\dfrac{v_{0}}{t_{0}}$$(t_{0}+t)$ $\dots (2\ast)$
とみれば,$\dfrac{v_{0}}{t_{0}}$を比例定数として$v$と$t_{0}+t$は比例関係にあります.
それでは,$t_{0}+t$は一体何者なのでしょうか??
実は,$t_{0}+t$は絶対温度なんです.
$t_{0}+t=T$とおくと,$(2\ast)$は
$v=\dfrac{v_{0}}{t_{0}}T$
$\dfrac{v}{T}=\dfrac{v_{0}}{t_{0}}=一定$
となり,いわゆるシャルルの法則が導かれます.
知ってのとおり,シャルルの法則(またはボイルシャルルの法則)では,絶対温度を使わなくてはいけません.
理由は,絶対温度にしないと体積と温度に比例関係がなくなってしまうからなんです.
ということで,答えは④です.



コメント