
前回の続きです.
今回は質量が異なる場合についてです.
前回の内容はこちら.
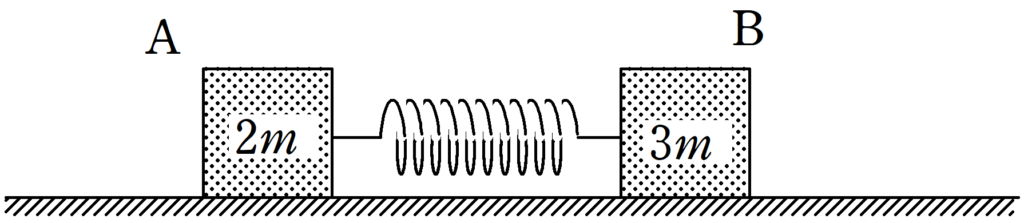
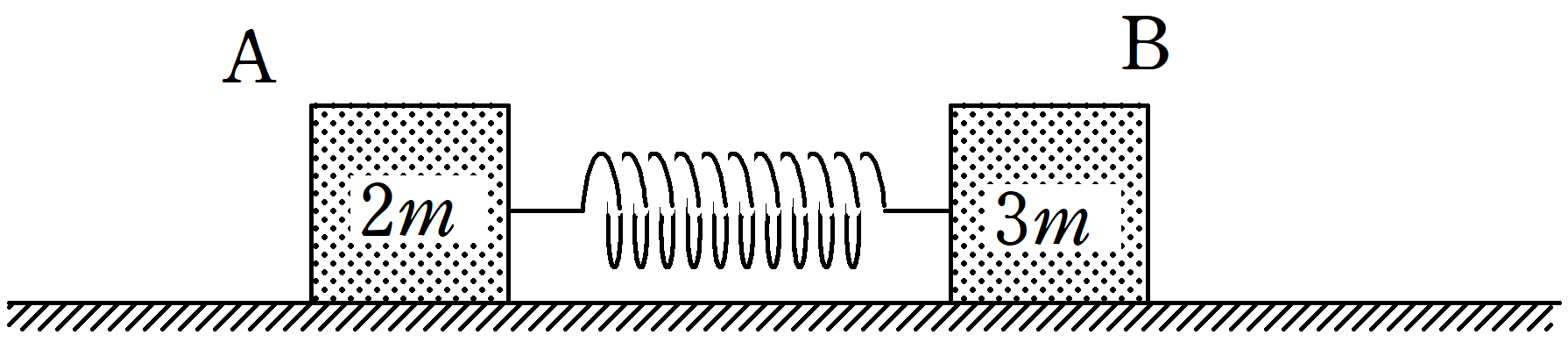
図のように水平で滑らかな床の上に質量$2m$,$3m$の2つ物体A,Bがばね定数$k$の軽いばねによってつながれている.
自然長の状態からAとBに力を加えてばねを$l$だけ伸ばして静かにはなした.
その後の運動について,次の問いに答えよ.
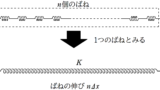
(1) AとBの重心でばねを分割して考える.A側のばね定数$k_{\rm A}$とB側のばね定数$k_{\rm B}$を求めよ.
(2) 重心から見たBの運動について考える.自然長の位置を原点として,ばねが伸びる方向に座標をとる.はじめ,重心から見たB側のばねはどれほど伸びていたか.$l$を用いて答えよ.
(3) B側の物体の運動方程式を立てることによって,重心からみたBの角振動数$\omega_{\rm B}$を求めよ.
(4) 同じく,A側の物体の角振動数$\omega_{\rm A}$を求めよ.
(5) 手をはなした時刻を$t=0$とする.時刻$t$におけるAとBの速度を求めよ.ただし,速度の向きは上図の右方向を正とする.
(6) 重心からみた運動量の和が0であることを確かめよ.
<解答>
(1)

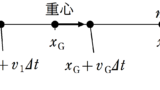
この問題でも,前回と同様に重心の初速度は0で,重心の加速度も0なので,重心は常に静止しています.
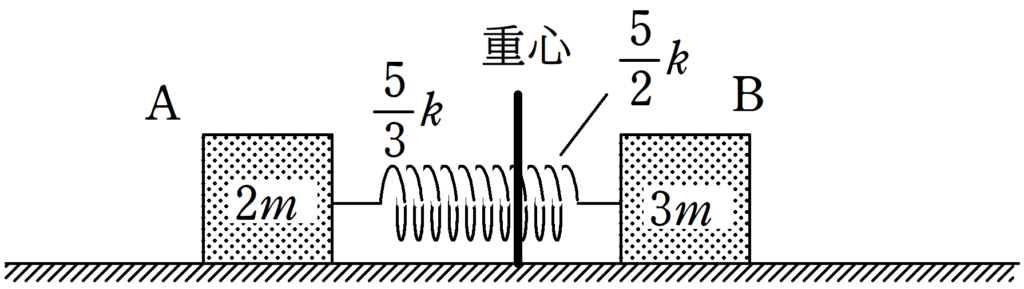

重心はABを$3:2$に内分した場所にあるね.
だから,重心の左側のばねの長さと右側の長さの比は$3:2$です.
ばね定数は長さに反比例することから次の計算ができます.
ちなみに,なぜ,ばね定数は長さに反比例するのかを知りたい人は,次の記事を読んでみてください.
★ ばね定数を求める.
A側のばね定数について
$k:k_{\rm A}=1:\dfrac{1}{\dfrac{3}{5}}$
$\therefore$ $k_{\rm A}=\dfrac{5}{3}k$
B側のばね定数について
$k:k_{\rm B}=1:\dfrac{1}{\dfrac{2}{5}}$
$\therefore$ $k_{\rm B}=\dfrac{5}{2}k$
(2)
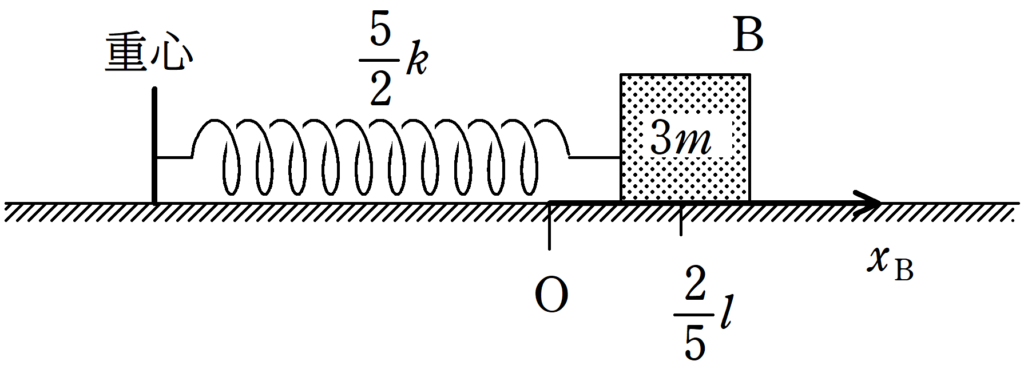

材質が同じで軽いばねは,力を加えると各部分が均等に伸びます.
つまり,ばねが長ければ長いほど伸びが大きくなります.
いま,A側のばねとB側のばねの長さの比が$3:2$なので,はじめの伸びも$3:2$となります.
ばね全体の伸びが$l$なので,A側のばねの伸びは$\dfrac{3}{5}l$,B側のばねの伸びは$\dfrac{2}{5}l$となります.
(3)
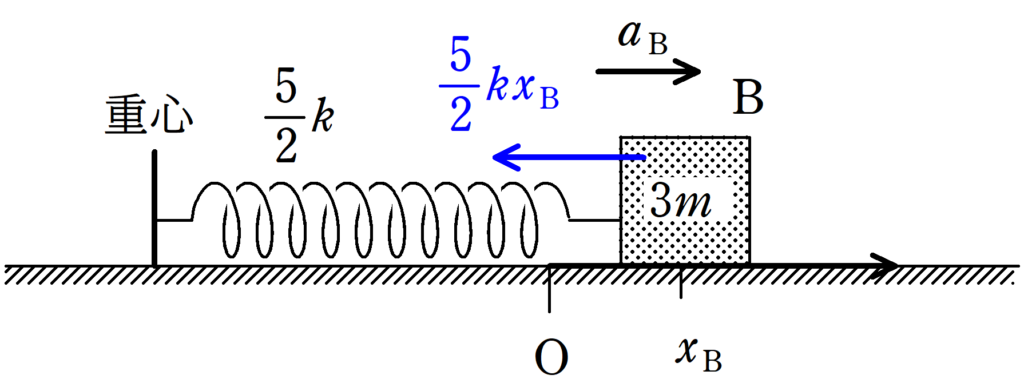

さあ,運動方程式を立てましょう.
問題文の指定通り,自然長となる位置を原点ととり,伸びる方向を正とします.
Bが座標$x_{\rm B}$にあるときの加速度を$a_{\rm B}$とします.
このとき,Bにはたらく水平方向の力は弾性力のみですね.
★ 物体Bの運動方程式
$3ma_{\rm B}=-\dfrac{5}{2}kx_{\rm B}$

この運動方程式から,中心座標は$x_{\rm B}=0$,角振動数$\omega_{\rm B}$は
$\omega_{\rm B}=\sqrt{\dfrac{5k}{6m}}$
周期$T_{\rm B}$は
$T_{\rm B}=2\pi\sqrt{\dfrac{6m}{5k}}$
また,中心から右端までの距離が$\dfrac{2}{5}l$なので,振幅は$\dfrac{2}{5}l$となります.
ついでに,手をはなした時刻を$t=0$とすれば,時刻$t$におけるBの座標$x_{\rm B}$の位置は
$x_{\rm B}=\dfrac{2}{5}l\cos\sqrt{\dfrac{5k}{6m}}t$ $\dots (\ast)$
です!
(4)
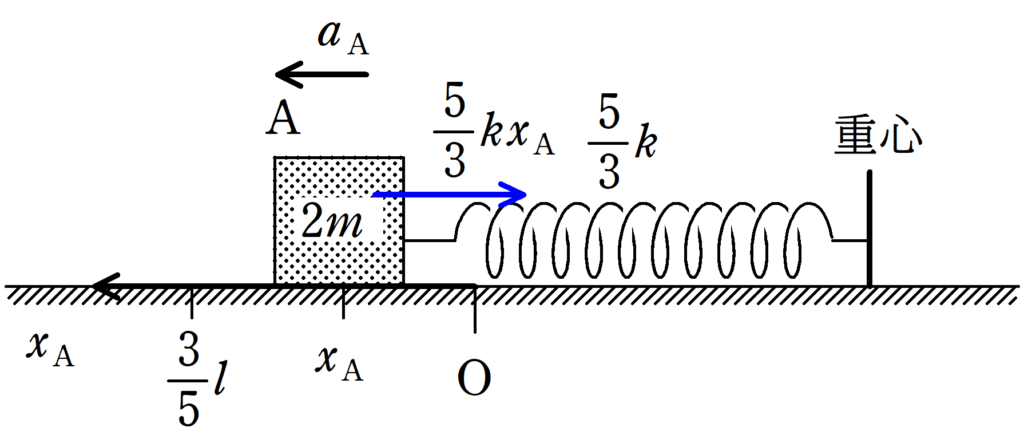

同じく,Aの方の運動方程式も立てましょう.
自然長の位置を原点として,伸びる方向に座標をとります.
位置$x_{\rm A}$における加速度を$a_{\rm A}$として,
★ 物体Aの運動方程式
$2ma_{\rm A}=-\dfrac{5}{3}kx_{\rm A}$

この運動方程式から,中心座標は$x_{\rm A}=0$,角振動数$\omega_{\rm A}$は
$\omega_{\rm A}=\sqrt{\dfrac{5k}{6m}}$
となります.
$\omega_{\rm A}=\omega_{\rm B}$となってるね!
だから,周期も同じ$T_{\rm A}=2\pi\sqrt{\dfrac{6m}{5k}}$となります.
振幅は$\dfrac{3}{5}l$なので,時刻$t$における座標$x_{\rm A}$は
$x_{\rm A}=\dfrac{3}{5}l\cos\sqrt{\dfrac{5k}{6m}}t$ $\dots (2\ast)$
となります.
(5)

(3)(4)で求めた$(\ast)$と$(2\ast)$の式
$x_{\rm B}=\dfrac{2}{5}l\cos\sqrt{\dfrac{5k}{6m}}t$
と
$x_{\rm A}=\dfrac{3}{5}l\cos\sqrt{\dfrac{5k}{6m}}t$
をそれぞれ$t$微分すれば速度ができますが,ここで注意することがあります.
Aの座標は左方向を正としましたが,問題文では,右方向が正であると指定されています.
なので,$(2\ast)$の式を$t$で微分をした後に座標が逆向きであることを考慮してさらに$-$をとる必要があります.

こういうのは”あるある”だよね.
自分の設定したものと問題文の設定がことなるっていう..
じゃあ,
$\dfrac{dx_{\rm B}}{dt}=-\dfrac{2}{5}l\sqrt{\dfrac{5k}{6m}}\sin\sqrt{\dfrac{5k}{6m}}t$
$\dfrac{dx_{\rm A}}{dt}=-\dfrac{3}{5}l\sqrt{\dfrac{5k}{6m}}\sin\sqrt{\dfrac{5k}{6m}}t$
から,BとAの速度$v_{\rm B}$と$v_{\rm A}$はそれぞれ
$v_{\rm B}=\dfrac{dx_{\rm B}}{dt}=-\dfrac{2}{5}l\sqrt{\dfrac{5k}{6m}}\sin\sqrt{\dfrac{5k}{6m}}t$
$v_{\rm A}=-\dfrac{dx_{\rm A}}{dt}=\dfrac{3}{5}l\sqrt{\dfrac{5k}{6m}}\sin\sqrt{\dfrac{5k}{6m}}t$
となるんだね.
(6)

最後に,重心からみた運動量の和が0であることを確かめます.
実際はこれを用いて(5)を求めてもよいです.
重心からみた運動量の和が0になる理由がわからない方は,こちらの記事を読んでみてください.
★ 重心から見た運動量の和
$\eqalign{3mv_{\rm B}+2mv_{\rm A}&=3m(-\dfrac{2}{5}l\sqrt{\dfrac{5k}{6m}}\sin\sqrt{\dfrac{5k}{6m}}t)+2m(\dfrac{3}{5}l\sqrt{\dfrac{5k}{6m}}\sin\sqrt{\dfrac{5k}{6m}}t)\\&=0}$

確かに運動量の和は0となったね!
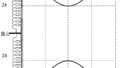
ちなみに今回は時間とともに次の振動します.
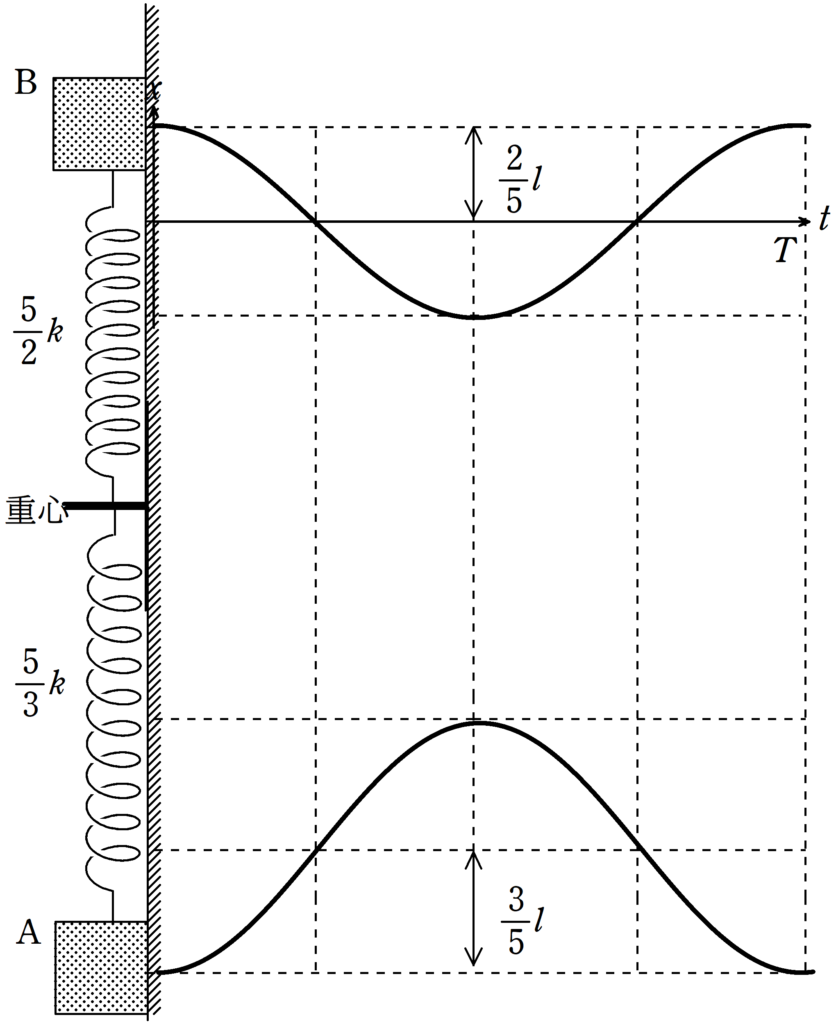


コメント
[…] [発展]単振動の演習問題② 2つの物体の単振動②(質量が異なる場合)NEKO… 問題 […]