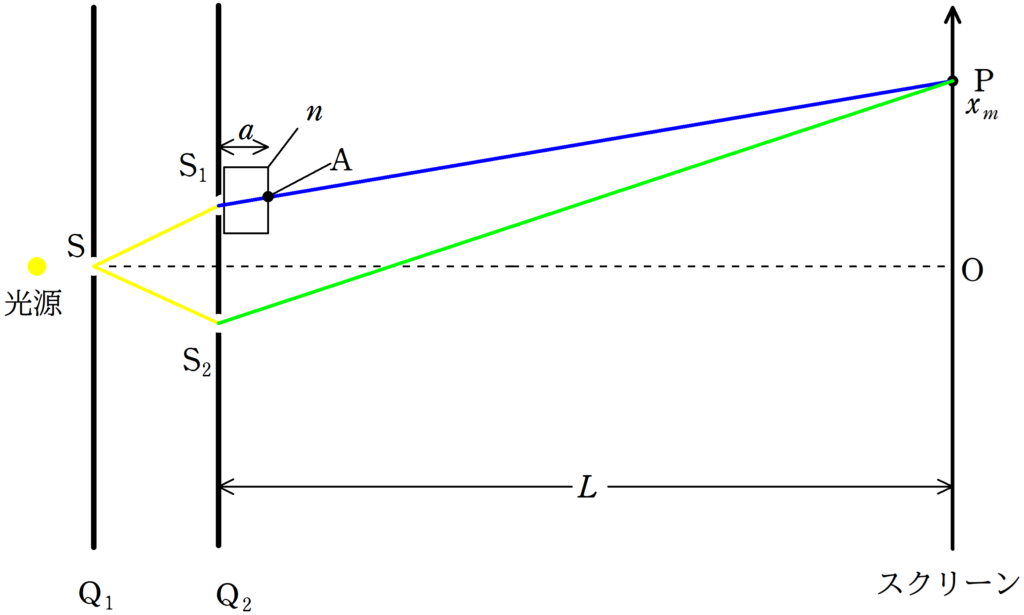
ついたて$\rm Q_{1}$,$\rm Q_{2}$,スクリーンが平行に設置されている.
$\rm Q_{2}$とスクリーンの距離は$L$である.
$\rm Q_{2}$には間隔$d$のスリットがあり,スリットの垂直二等分線と$\rm Q_{1}$との交点にスリット$\rm S$がある.
2スリット$\rm S_{1}$,$\rm S_{2}$の垂直2等分線とスクリーンとの交点を原点$\rm O$としスクリーン上に$x$軸をとる.
スリット$\rm S$の左側より,波長$\lambda$の単色光を当てたところ,スクリーンに明暗の縞模様ができた.
この状態から,スリット$\rm S_{1}$の後方(右)に厚さ$a$,空気に対する相対屈折率$n$の薄膜をおいたところ,明暗の縞模様が移動した.
縞模様はどの方向に,どれだけ移動したか.
ただし,$d$は$L$に比べて十分小さいとする.
<解答>

こちらは前回の内容です.
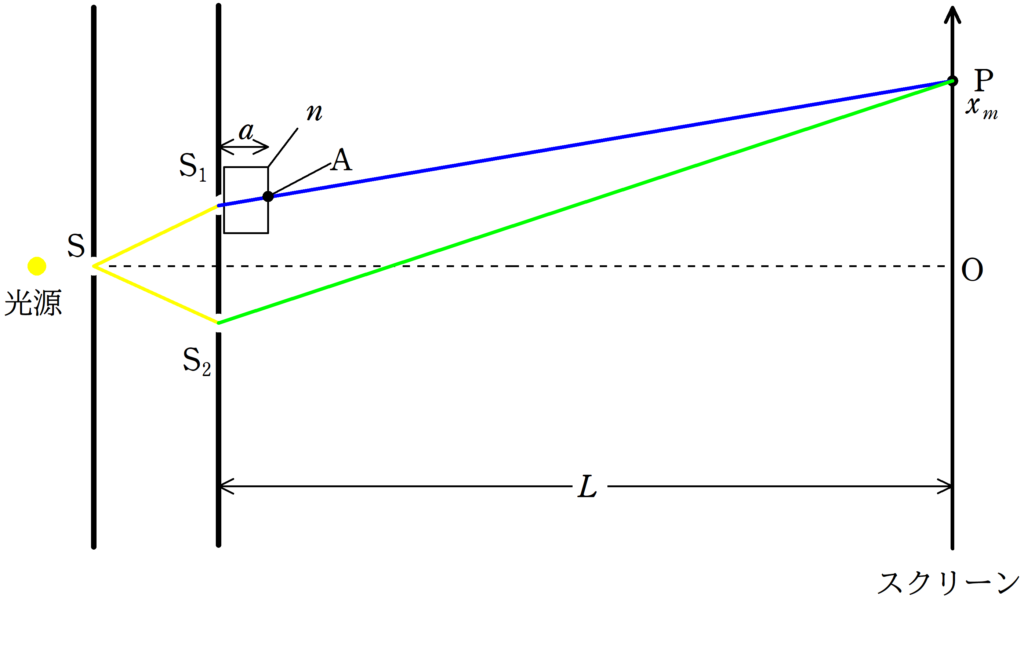

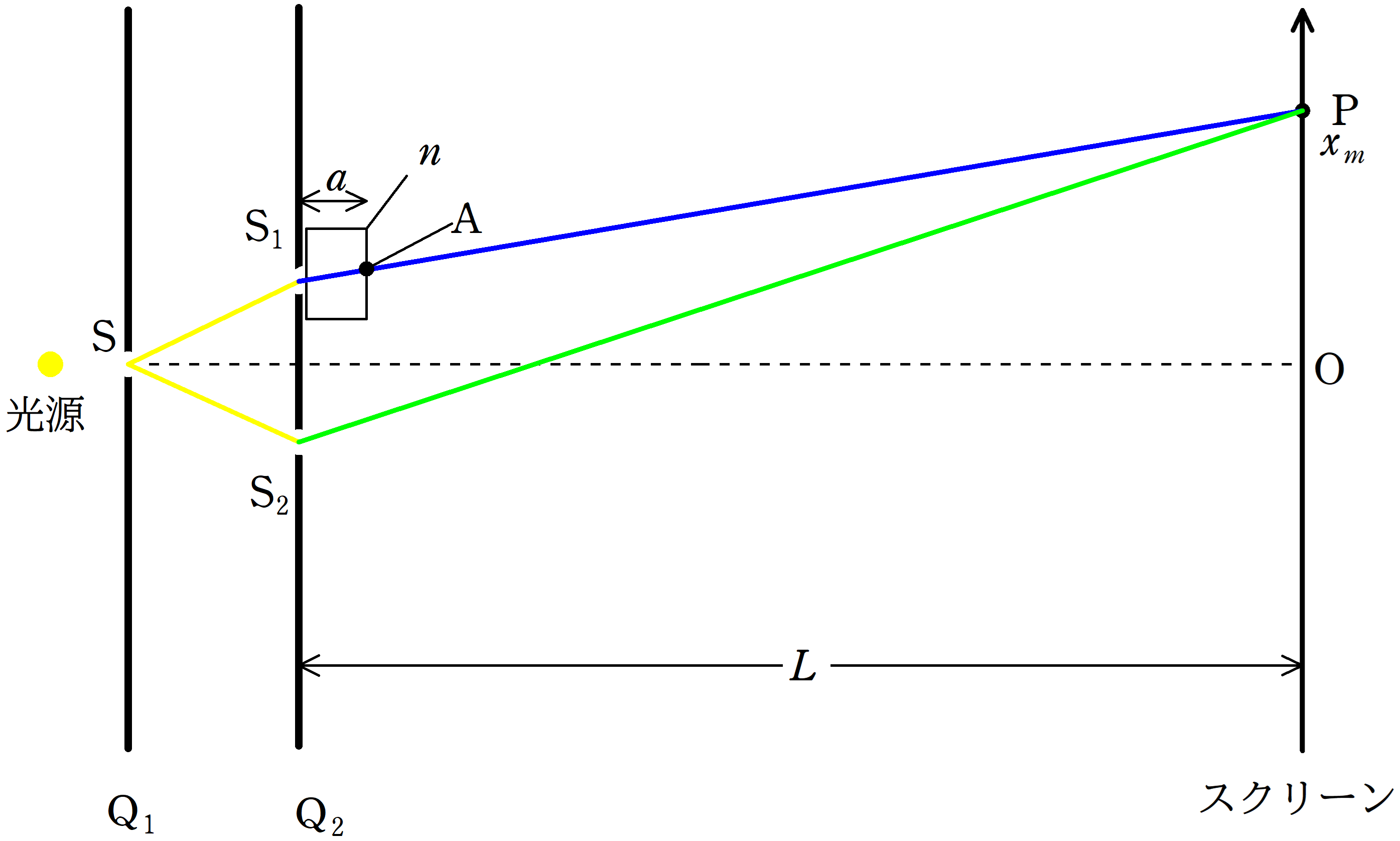
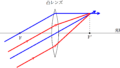
上図において,緑の方の経路の波の数$N_{緑}$は
$N_{緑}=\dfrac{\rm S_{2}P}{\lambda}$
です.
そして,青の方の経路の波の数$N_{青}$は
$N_{青}=\dfrac{\rm S_{1}A}{\dfrac{\lambda}{n}}+\dfrac{\rm AP}{\lambda}$
そして,今まで通り,次数$m$を使って,明線条件は次のようになるね.
$N_{緑}-V_{青}=m$
$\dfrac{\rm S_{2}P}{\lambda}-\left(\dfrac{\rm S_{1}A}{\dfrac{\lambda}{n}}+\dfrac{\rm AP}{\lambda}\right)$ $\dots (\ast)$

そうですね.
ところで,今までの演習問題でずっと使ってきた近似式
${\rm S_{2}P-S_{1}P}\approx d\dfrac{x_{m}}{L}$
を使いたいと思うのですが,$(\ast)$どのように変形すればよいでしょうか.

$\rm AP$を$\rm {AP=S_{1}P-S_{1}A}$とすればいいのかな?

そうですね,それでは,計算を実行していきましょう.
$\eqalign{\dfrac{\rm S_{2}P}{\lambda}-\left(\dfrac{\rm S_{1}A}{\dfrac{\lambda}{n}}+\dfrac{\rm S_{1}P-S_{1}A}{\lambda}\right)&=m\cr \dfrac{\rm S_{2}P}{\lambda}-\dfrac{n\cdot \rm S_{1}A}{\lambda}-\dfrac{\rm S_{1}P-\rm S_{1}A}{\lambda}&=m \cr ({\rm S_{2}P-S_{1}P})-n\cdot {\rm S_{1}A}+{\rm S_{1}A}&=m\lambda }$
${\rm S_{2}P-S_{1}P}=d\dfrac{x_{m}}{L}$,${\rm S_{1}A}=a$を代入して
$\eqalign{d\dfrac{x_{m}}{L}-(n-1)a&=m\lambda\cr x_{m}&=\dfrac{mL\lambda}{d}+\dfrac{L(n-1)a}{d}}$

もとの明線の位置は$x_{m}=\dfrac{mL\lambda}{d}$だったから,答えは$\dfrac{L(n-1)a}{d}$だけ上にずれる移動するですね!

コメント