
今回は凸面鏡の式です.
凸面鏡の式をどのように導出するかを確認します.
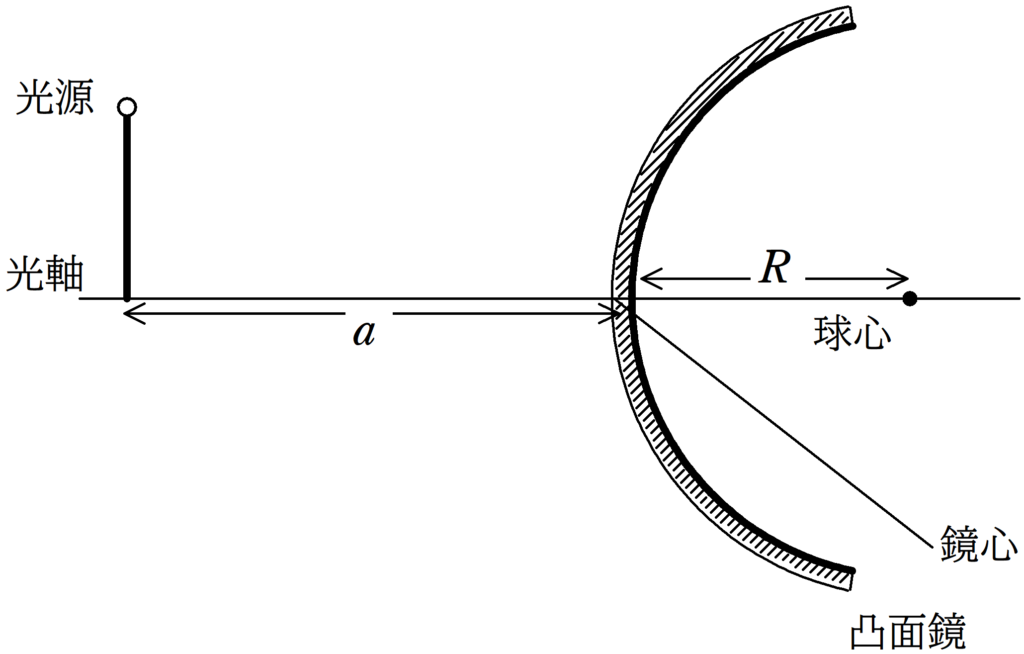
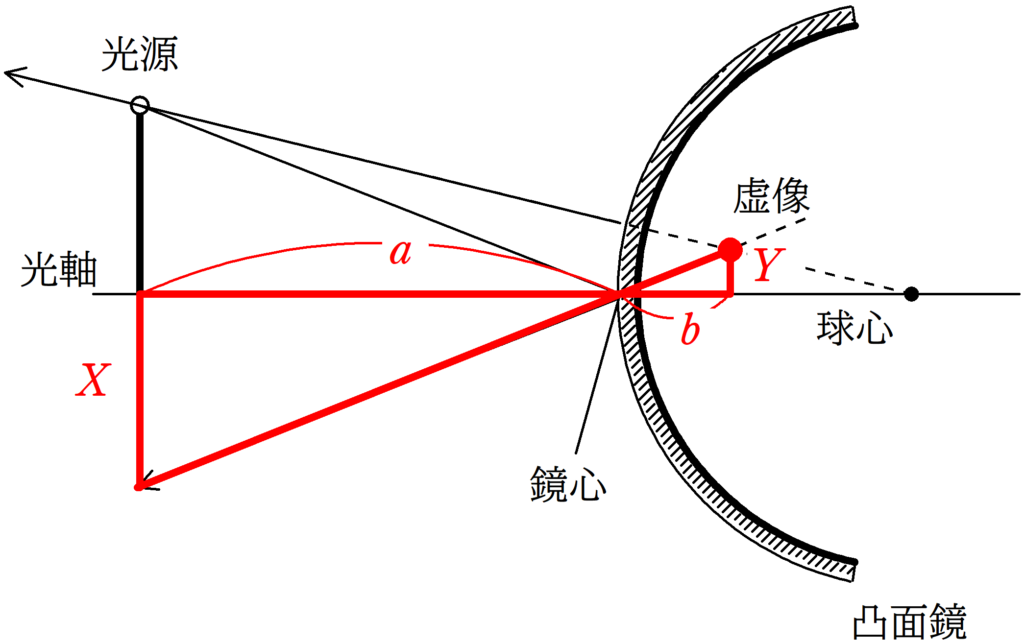
上図のように,凸面鏡と光源が設置されている.
凸面鏡の鏡心から光源までの距離を$a$,凸面鏡の曲率半径を$R$,光源が凸面鏡に反射することによってできる像と鏡心との距離を$b$とする.
このとき,$a, b , R$の関係式を導け.
<解答>

まずは,代表光線をかいて像を作図しましょう.
凸面鏡の代表光線は次の2つを覚えておきましょう.
1. 鏡心にあたる光は反射の法則にしたがって,反射する.
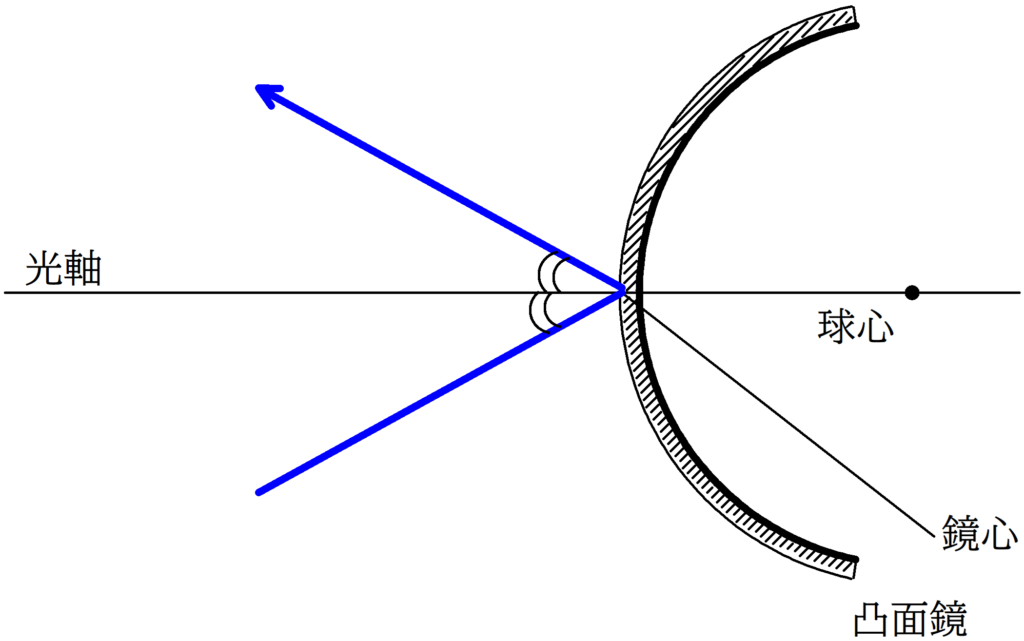
2. 球心を通る光線の入射角は90°なので,反射角も90°である.すなわち,反射光線は入射経路と同じ経路をたどる.
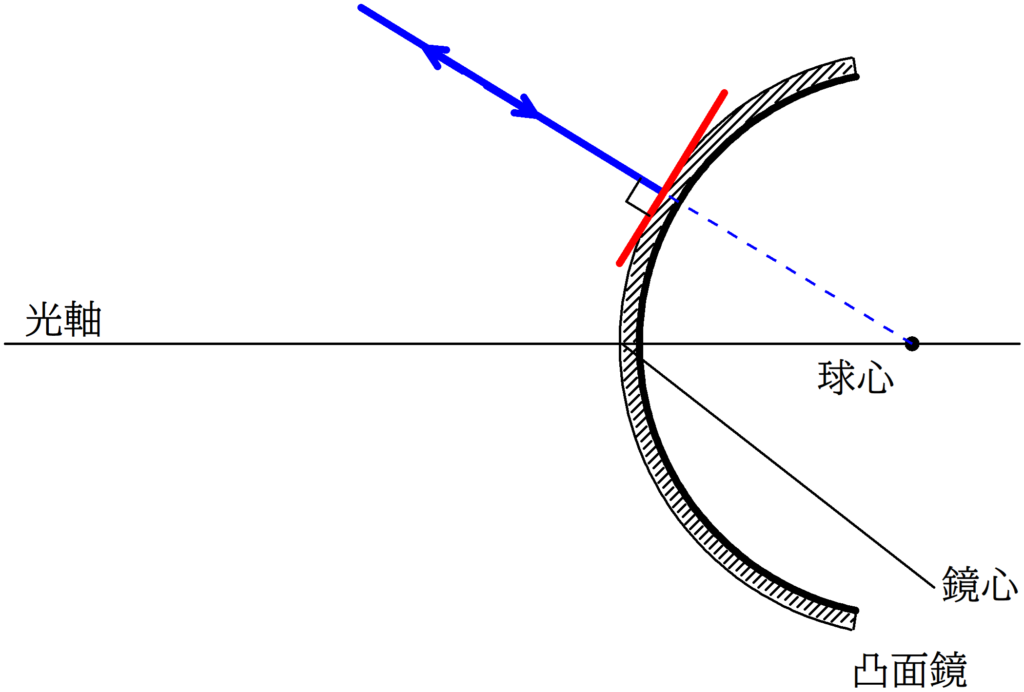
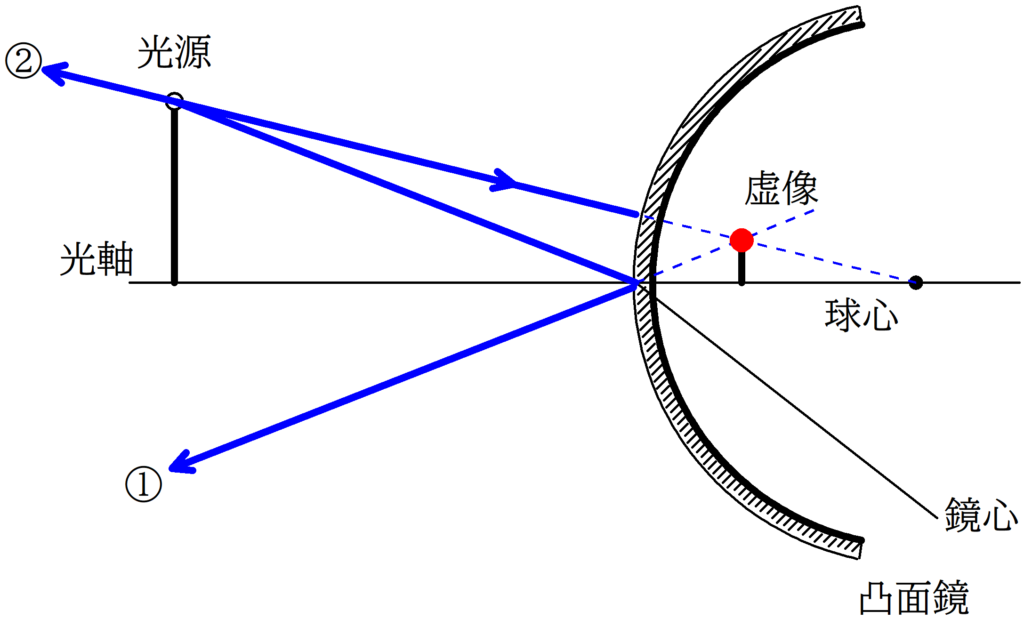

上図の①は鏡心にあたる光線で,②は球心に向かう光線だね.
これらの光線は反射後に交わらないので,反対側に線を伸ばして交点を探します.
交点(赤い点)が虚像です.
今までと同様に,光源の高さを$X$,虚像の高さを$Y$として,2組の相似な図形を見つけましょう.
\begin{enumerate}[(1)]
\end{enumerate}
★ 赤の相似比
$\dfrac{Y}{X}=\dfrac{b}{a}$ $\cdots (\ast)$
★ 緑の相似比
$\dfrac{Y}{X}=\dfrac{R-b}{a+R}$ $\cdots (2\ast)$
$(\ast),(2\ast)$より
$\eqalign{\dfrac{b}{a}&=\dfrac{R-b}{a+R}\cr b(a+R)&=a(R-b)\cr ab+bR&=aR-ab\cr bR-aR&=-2ab}$
両辺$abR$で割って
$\eqalign{\dfrac{bR}{abR}-\dfrac{aR}{abR}&=\dfrac{-2ab}{abR}\cr \dfrac{1}{a}-\dfrac{1}{b}&=-\dfrac{2}{R}}$
したがって,
$\dfrac{1}{a}-\dfrac{1}{b}=-\dfrac{2}{R}$

レンズの式の対応させて符号の意味を考えると
$a\dots$ 実光源だから正
$b\dots$ 虚像がだから負
ってことかな?
とすると,凹面鏡のときは$R>0$で,凸面鏡のときは$R<0$となるんだね.

そういうことですね.
そして,凹面鏡と同様に,焦点の場所を探しましょう.
$a\rightarrow \infty$のときに平行光線とみなすことができます.
このとき,反射されて光軸と交わる位置を焦点とします.
$a\rightarrow \infty$のとき,$b\rightarrow f$として
$a\rightarrow \infty$のとき,$\dfrac{1}{a}\rightarrow 0$より
$\eqalign{0-\dfrac{1}{f}&=-\dfrac{2}{R}\cr f&=\dfrac{R}{2}}$

焦点は鏡心と球心の中点にあるんだね!
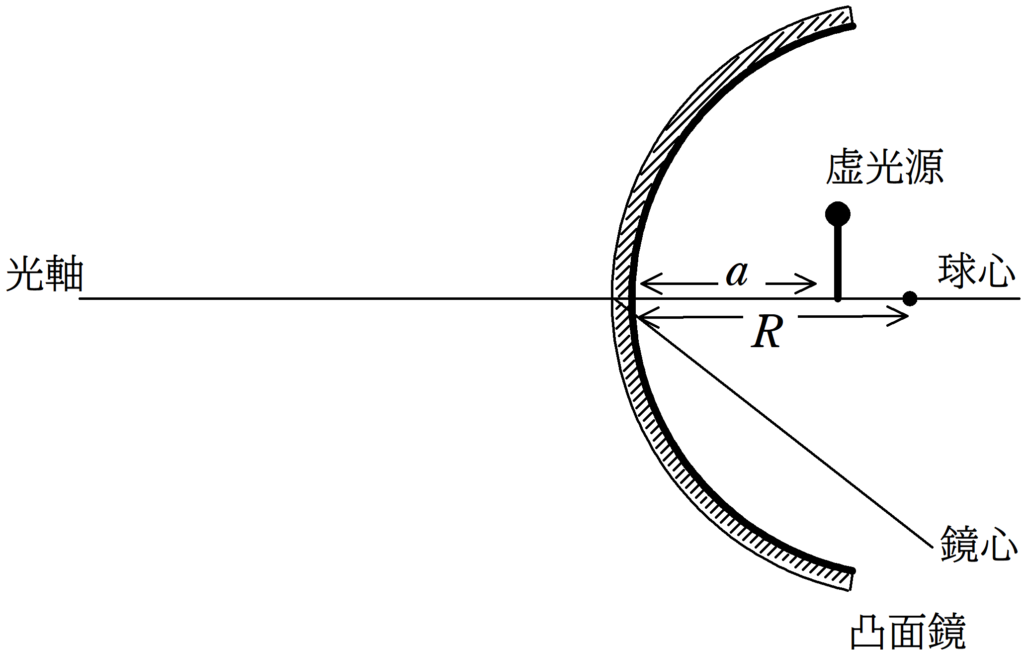
次の(1),(2)について,鏡心から虚光源までの距離は$a$,曲率半径が$R$であるとする.
鏡心からできる像までの距離を$b$としたとき,$a , b , R$の関係式をそれぞれ導け.
(1)
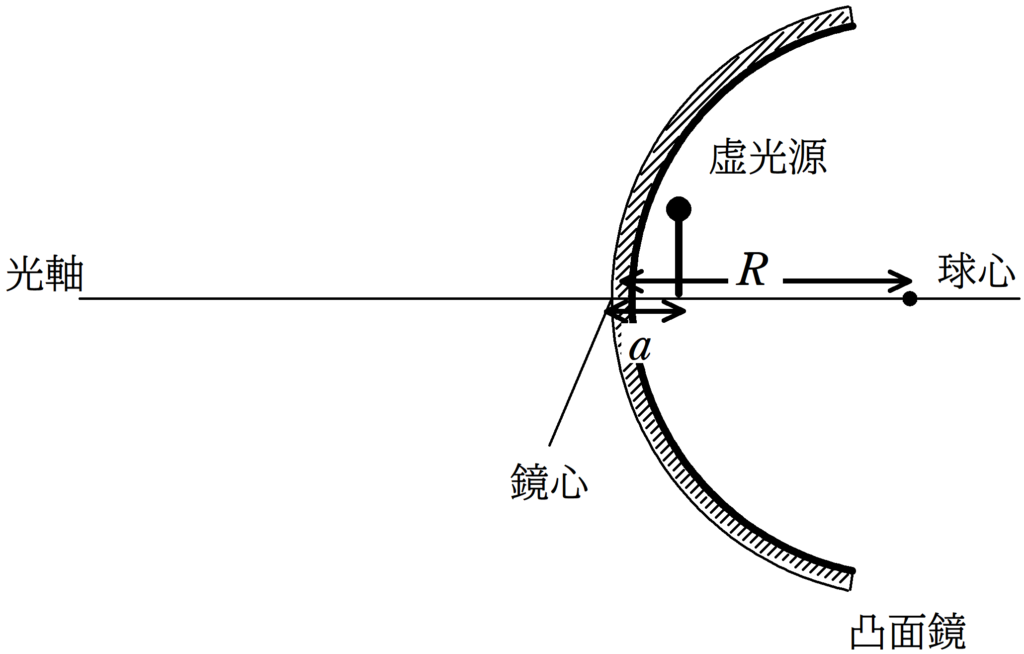
(2)
<解答>
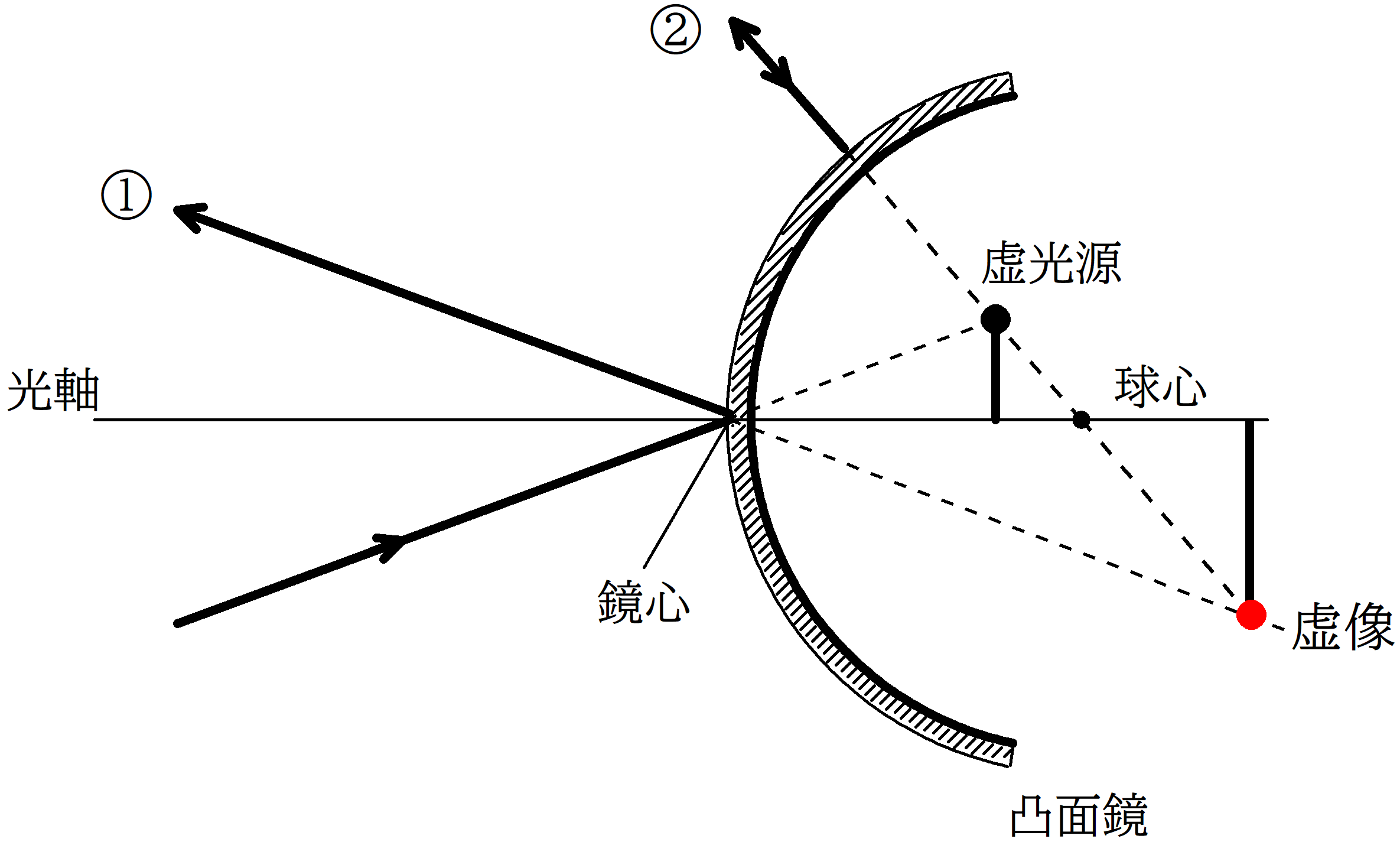
(1)

鏡がなかったらできていた像を,虚物体または虚光源といいます.
このとき,すべての光は虚光源に向かうように鏡に入射します.

じゃあ,虚光源に向かう光線のうち,
①:鏡心にあたる光線
②:球心に向かう光線
を作図して交点を求めればいいんだね.
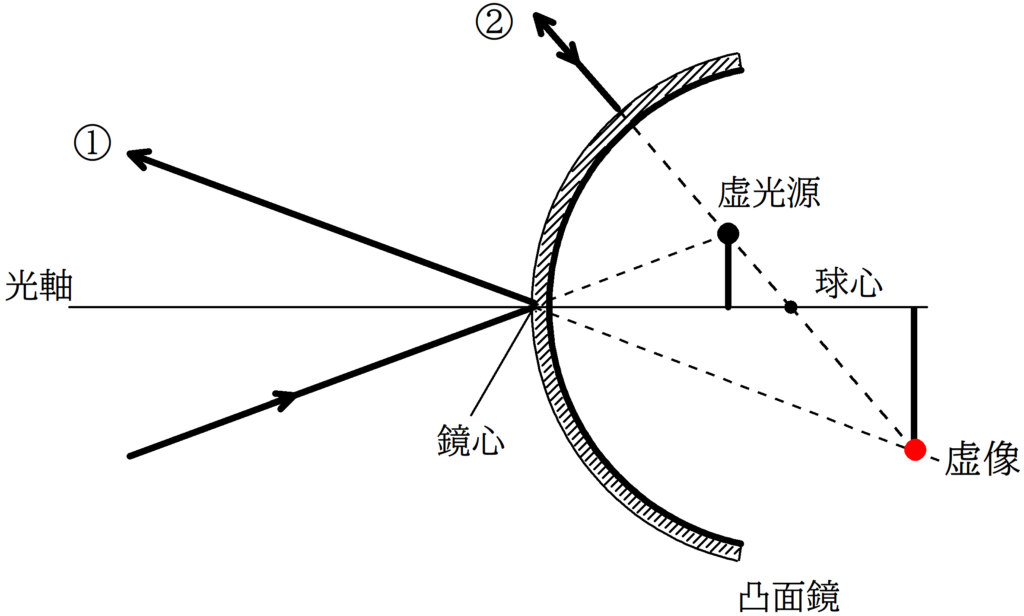

すると反射光線が交わらないので,反対側に線を伸ばすと交点を確認できます.
上図の赤い点が虚像となり,すべての入射光線は虚像から飛び出したように反射していきます.
虚光源の高さを$X$,虚像の高さを$Y$として相似な三角形を2組見つけましょう.
下図の赤い方の相似な三角形はやや見つけづらいですが,入射角と反射角が等しいことから合同な三角形を見つけて相似な三角形を探しましょう.
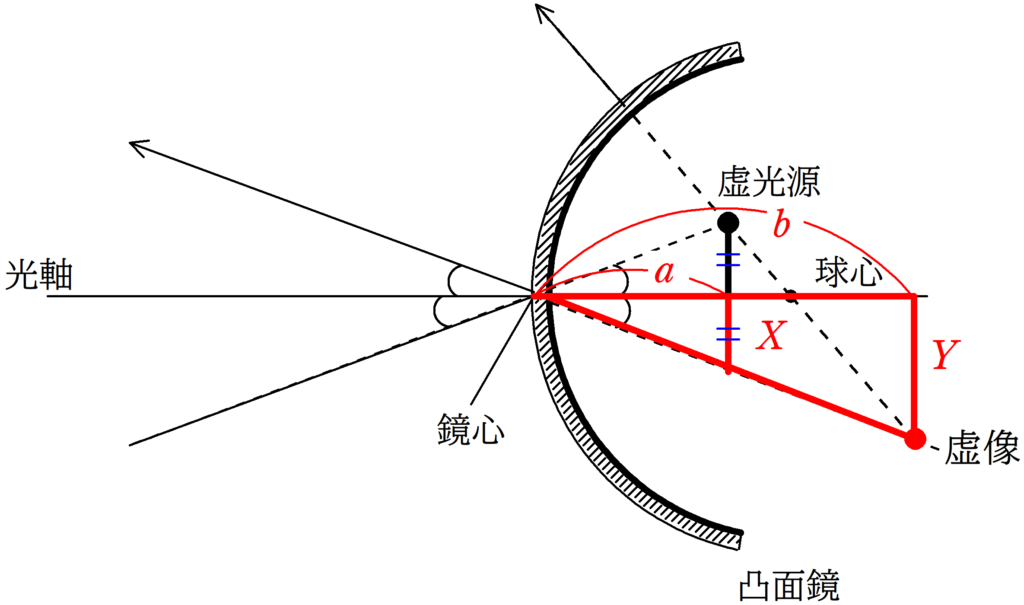
★ 赤い方の相似比
$\dfrac{Y}{X}=\dfrac{b}{a}$ $\cdots (5\ast)$
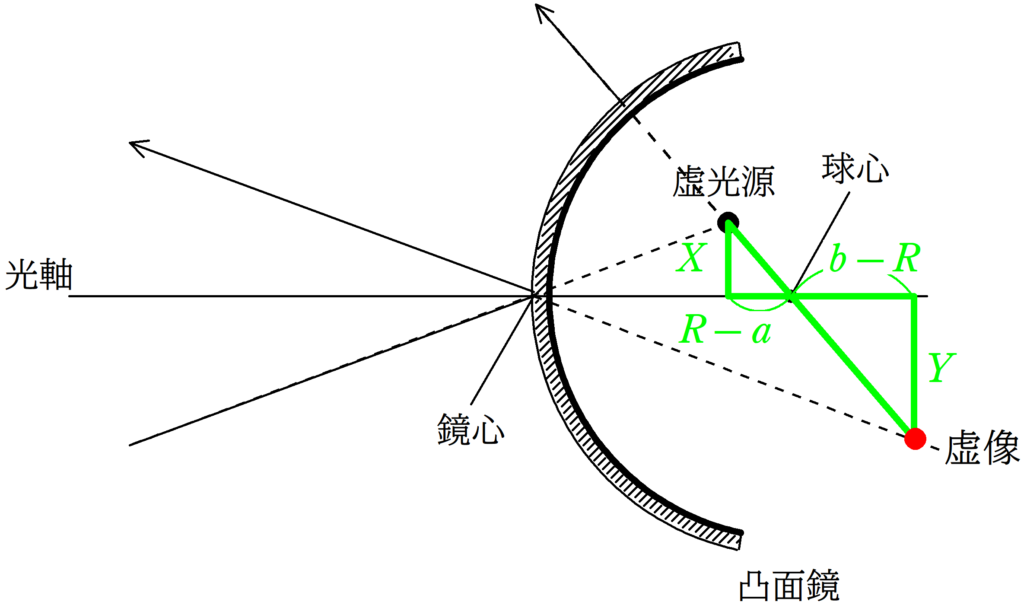
★ 緑の方の相似比
$\dfrac{Y}{X}=\dfrac{b-R}{R-a}$ $\cdots (6\ast)$
$(5\ast) , (6\ast)$より
$\eqalign{\dfrac{b}{a}&=\dfrac{b-R}{R-a}\cr b(R-a)&=a(b-R)\cr bR-ab&=ab-aR\cr -bR-aR&=-2ab}$
両辺$abR$で割って
$-\dfrac{1}{a}-\dfrac{1}{b}=-\dfrac{2}{R}$

それぞれの係数の符号は
$a\dots$ 虚光源だから負
$b\dots$ 虚像だから負
$R\dots$ 凸面鏡だから負
なんだね.
(2)

(2)も同様に作図して相似比を考えてみよう.
代表光線は
①:鏡心にあたる光線
②:球心に向かう光線
です.
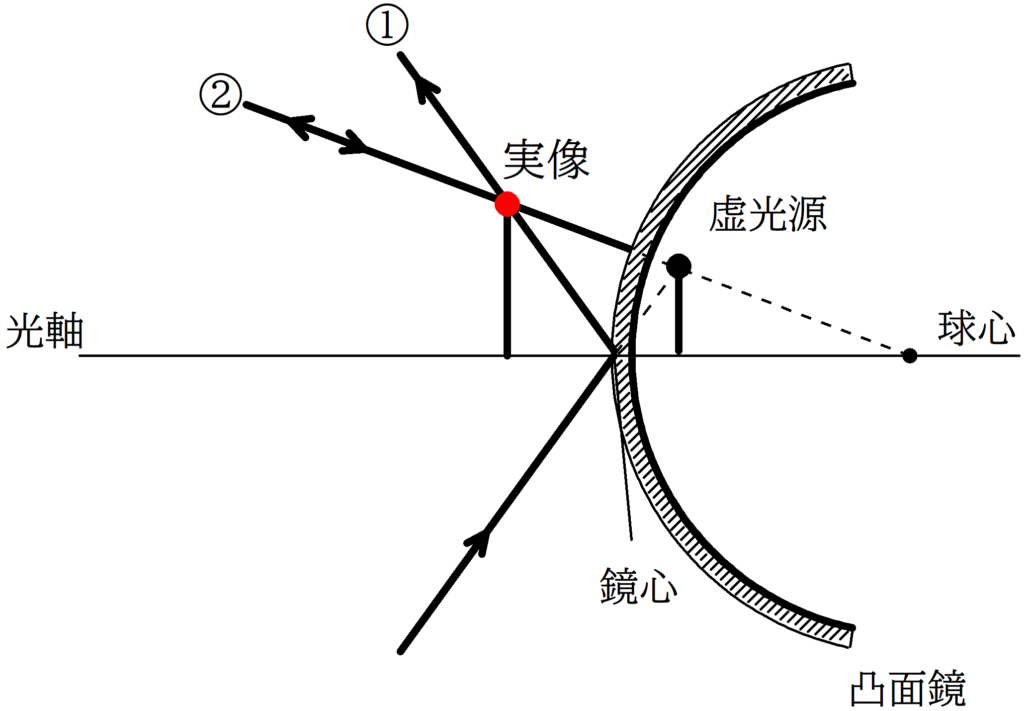

すると,反射光線が交わる場所(上図赤い点)に実像ができます.
すべての光線は反射後,実像を通るように進みます.
次に虚光源の高さを$X$,実像の高さを$Y$として2組の相似な図形を探しましょう.
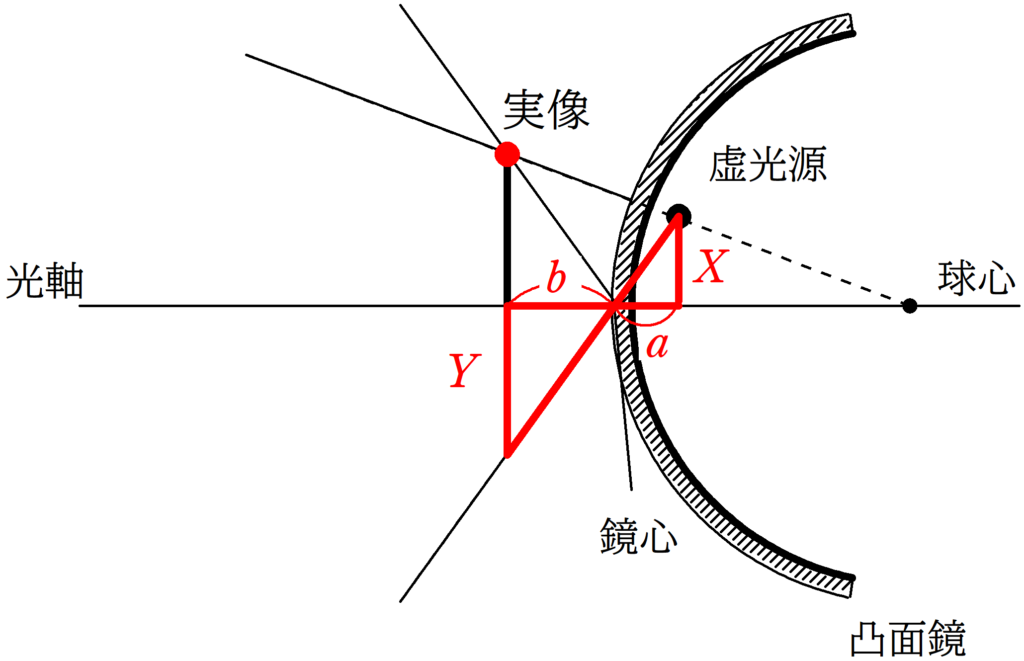
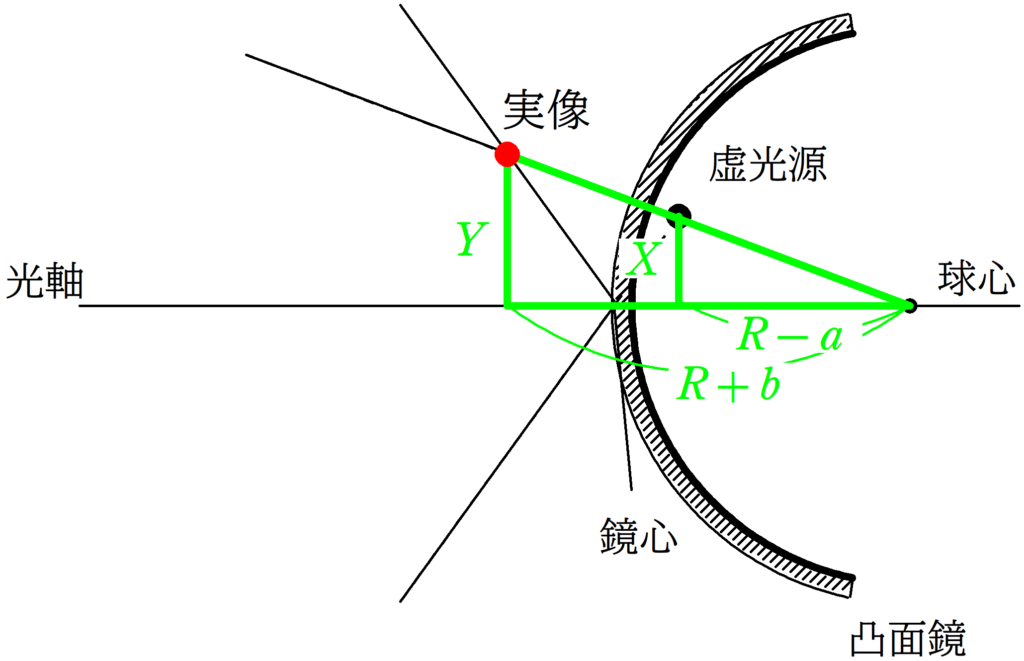
★ 赤の方の相似比
$\dfrac{Y}{X}=\dfrac{b}{a}$ $\cdots (7\ast)$
★ 緑の方相似比
$\dfrac{Y}{X}=\dfrac{R+b}{R-a}$ $\cdots (8\ast)$
$\eqalign{\dfrac{b}{a}&=\dfrac{R+b}{R-a}\cr b(R-a)&=a(R+b)\cr bR-ab&=aR+ab\cr -bR+aR&=-2ab}$
両辺$abR$で割って
$-\dfrac{1}{a}+\dfrac{1}{b}=-\dfrac{2}{R}$

それぞれの係数の符号は
$a\dots$ 虚光源だから負
$b\dots$ 実像だから正
$R\dots$ 凸面鏡だから負
なんだね.

それでは,最後に,球面鏡の式をまとめていきたいと思います.
球面鏡の鏡心と光源との距離を$|a|$,焦点距離を$|f|$,球面鏡の曲率半径を$|R|$,像との距離を$|b|$とする.
このとき,次の式が成り立つ.
$\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{f}=\dfrac{2}{R}$
ただし,次の規則で$a$と$b$と$f$の正負を決める.
$a>0 \dots$ 実物体(実光源), $a<0 \dots$ 虚物体(虚光源)
$b>0 \dots$ 実像, $b<0 \dots$ 虚像
$f>0 \dots$ 凹面鏡, $f<0 \dots$ 凸面鏡


コメント