
前回は,平面波が干渉して,どのような腹線や節線ができるかの話をしました.
まずは,こちらからお読みください.

そして,今回は,腹線と腹線の距離を求める問題です.
これは意外と間違いが多いので,油断せずに問題を解いてみてください.
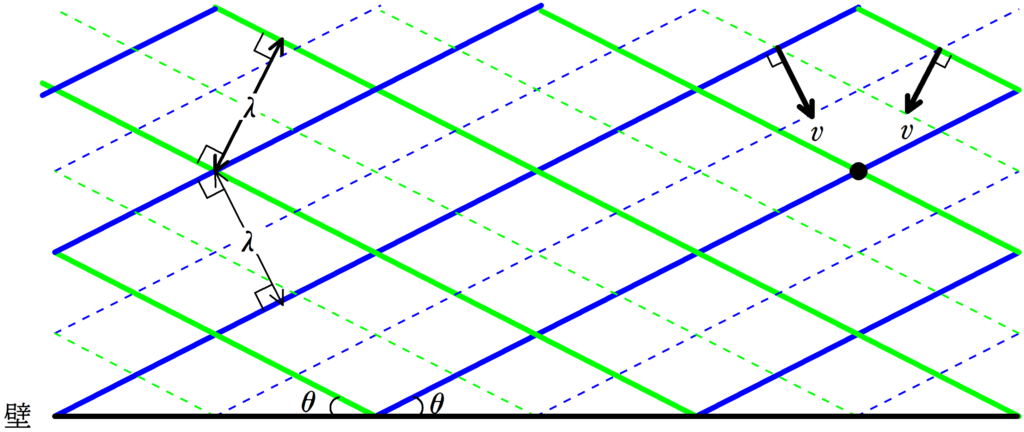
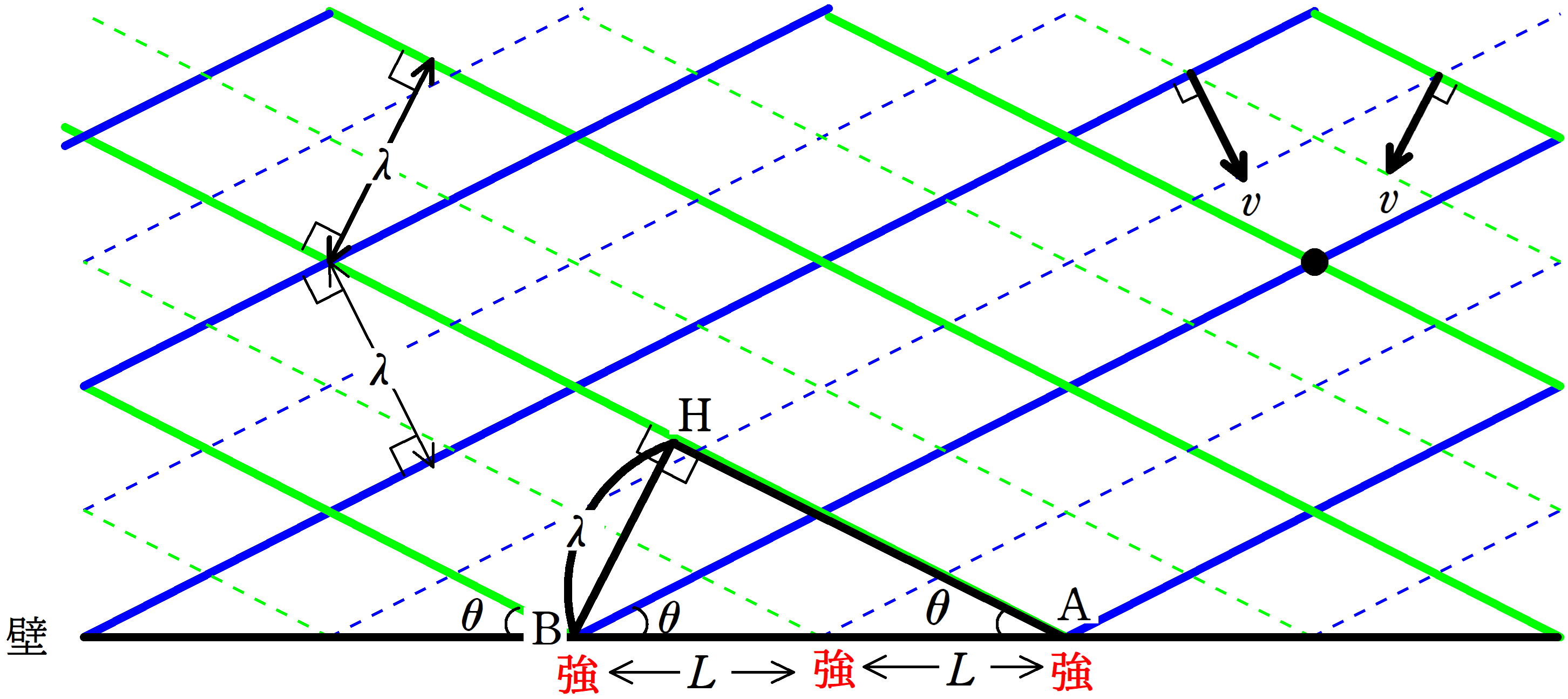
上図のような,青の平面波と緑の平面波が速さ$v$で進行している.
2つの平面波は壁からのなす角$\theta$であり,波長は$\lambda$である.
このとき,となり合う腹線と腹線の距離を$\lambda$と$\theta$を用いて表せ.
ただし,壁における反射は無視をする.
<解答>
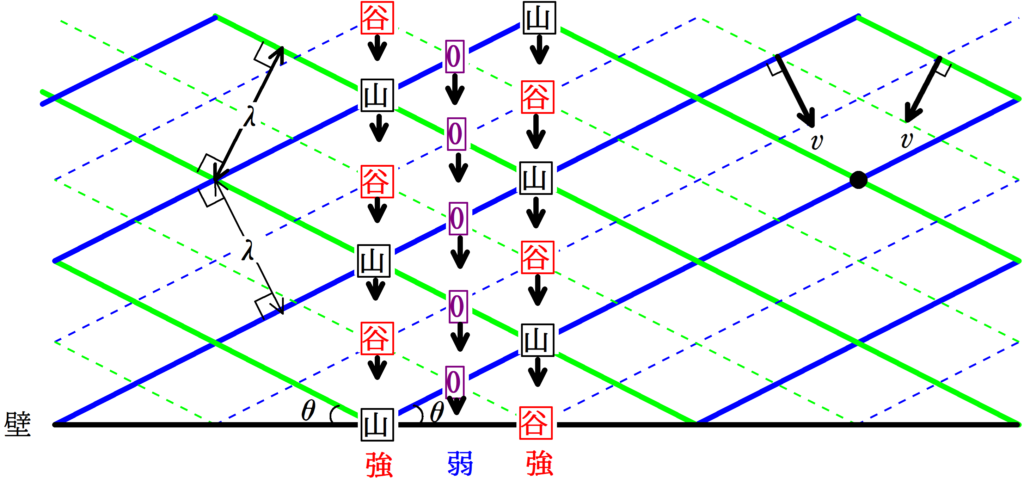

まずは,前回同様に,山と谷と,変位0の場所を確かめましょう.
そして,平面波の速度の向きから,次の瞬間の山や谷の位置を調べます.
そこから,腹線や節線の位置を調べることができます.
この場合,腹線は縦方向になるんでした.
この縦線の距離を求めましょう.
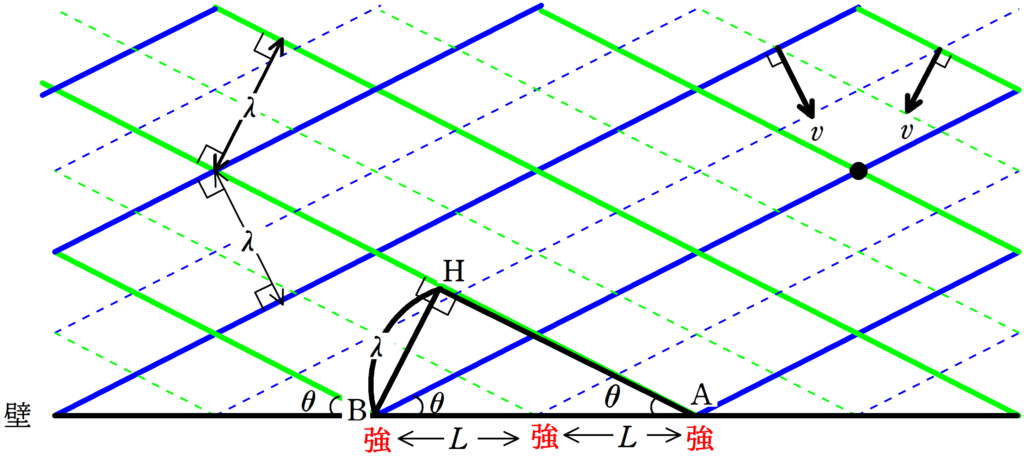

腹線と腹線の距離を$L$としましょう.
この$L$を求めるために,上図の$\rm \triangle ABH$を考えます.
${\rm AB}=2L$,${\rm BH}=\lambda$,$\angle \rm BAH=\theta$ですね.
このことから,次のように$L$を求めることができます.
★$\rm \triangle ABH$の三角比を考えて
$\sin \theta=\dfrac{\lambda}{2L}$
$\therefore$ $L=\dfrac{\lambda}{2\sin\theta}$

実際,解答をみるとなんてことないのですが,イチから自分で解くと苦戦するかもしれません.
さて,もう1題です!
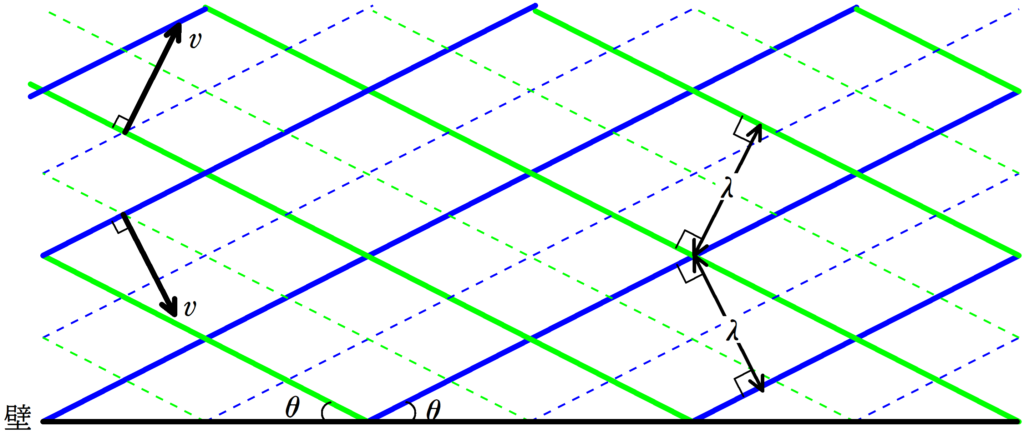
上図のような,青の平面波が速さ$v$で進行して,壁で反射される.
反射波の平面波は緑色で表していて,同じく速さ$v$で進行する.
2つの平面波は壁からのなす角$\theta$であり,波長は$\lambda$である.
このとき,となり合う腹線と腹線の距離を$\lambda$と$\theta$を用いて表せ.
<解答>
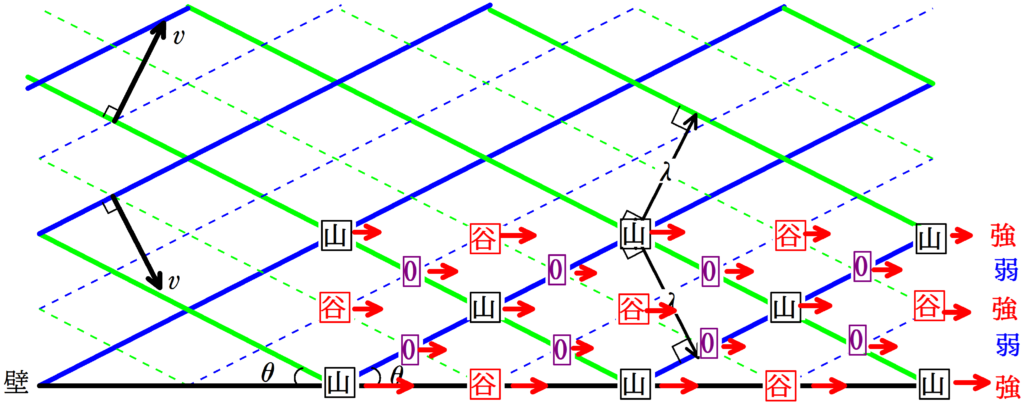
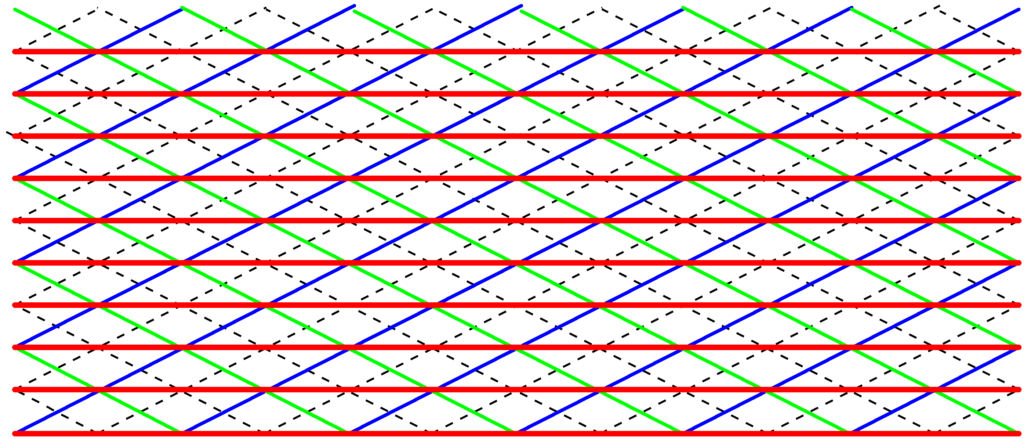

こちらは先ほど違い,山や谷が右方向に移動するので,腹線と節線はヨコ線になります.
では,腹線と腹線の距離を求めましょう.
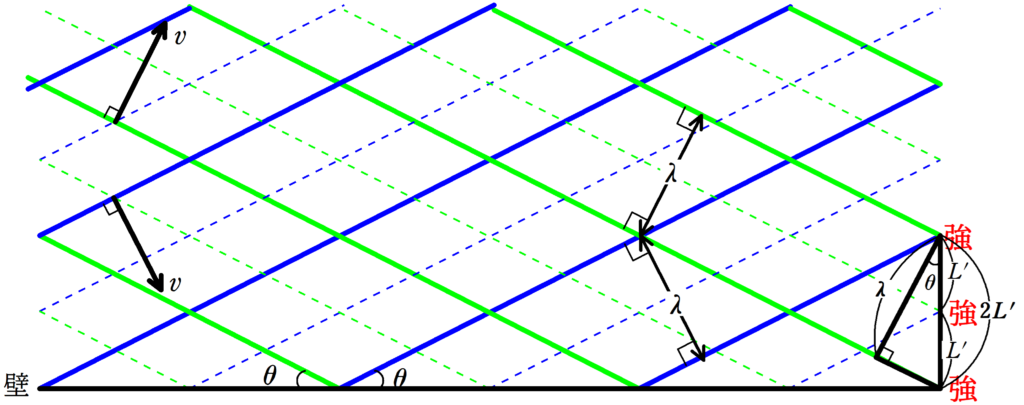

腹線と腹線の距離を$L^{\prime}$としましょう.
同じく,上図の直角三角形の三角比を考えましょう.
$\cos\theta =\dfrac{2L^{\prime}}{\lambda}$
$\therefore$ $L^{\prime}=\dfrac{\lambda}{2\cos\theta}$



コメント
[…] 平面波の演習問題② 腹線と腹線の距離を求めるNEKO前回は,平面波が干渉… […]