
今回は,気体の温度を一定に保ったまま変化する等温変化の問題です.
それでは,さっそく問題を解いてみましょう.
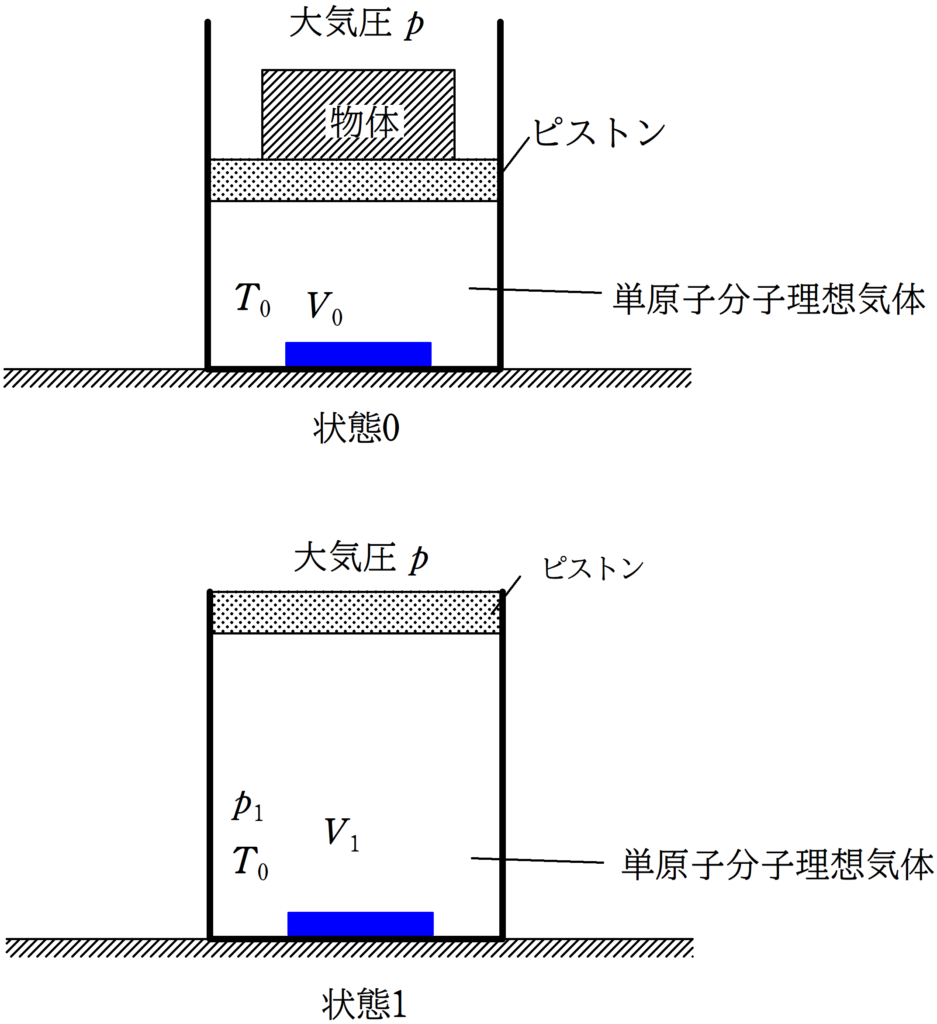
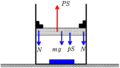
上図のように,水平な床の上に断熱容器が固定されている.
断熱容器の内側の底部には,温度調節器が設置されており,気体の温度を自由に調整できるようにしてある.
単原子分子理想気体を断熱容器となめらかなに動くことができる質量$m$で断面積$S$のピストンによって密封し,ピストンの上には質量$M$のおもりをのせる.
この状態を状態0とする.
状態0の単原子分子理想気体の体積は$V_{0}$,絶対温度は$T_{0}$であった.
この状態から温度を一定に保ちながらゆっくりとおもりをピストンの上から完全に取り除いた.
この状態を状態1とする.
このとき,次の問いに答えよ.
ただし,大気圧は$p$,重力加速度の大きさを$g$とする.
(1) 状態0における気体の圧力$p_{0}$を求めよ.
(2) 状態1における気体の圧力$p_{1}$と体積$V_{1}$を求めよ.
(3) 状態0から状態1までの間に気体が吸収した熱量を$Q$とする.気体がした仕事$W$を$Q$を用いて表せ.
<解答>
(1)

「圧力」を聞かれたときに,まっさきに思いついてほしいのが
可動部分のつり合いの式ですね!
- 可動部分のつり合いの式 → 力の情報が出てくる
- 理想気体の状態方程式(ボイルシャルルの法則)
- 熱力学第一法則 → エネルギーの情報が出てくる
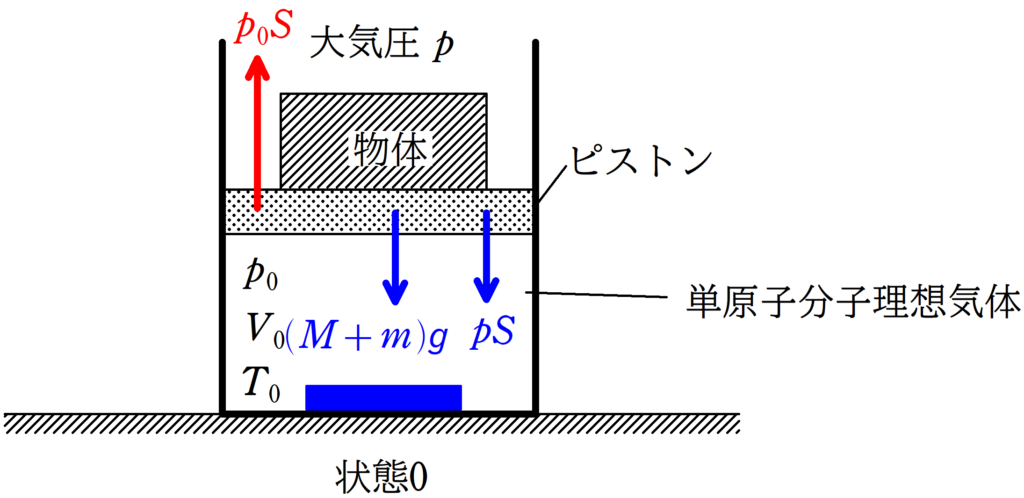
★ ピストンにはたらく力のつり合いの式
$p_{0}S=pS+(M+m)g$
$\therefore$ $p_{0}=p+\dfrac{M+m}{S}g$
(2)

同様に,まずは状態1における,ピストンにはたらく力のつり合いの式を立ててみましょう.
★ ピストンにはたらく力のつり合いの式
$p_{1}S=pS+mg$
$\therefore$ $p_{1}=p+\dfrac{mg}{S}$

そして,温度が一定なことから,状態0と状態1の間でボイルの法則を立ててみましょう.
理想気体について,物質量$n$が変化しないとき,気体の圧力を$p$,気体の体積を$V$,絶対温度を$T$とすると,
$\dfrac{pV}{T}=$一定
が成り立つ.(ボイル・シャルルの法則)
特に,温度が一定のとき
$pV=$一定(ボイルの法則)
圧力が一定のとき
$\dfrac{V}{T}=$一定(シャルルの法則)
が成り立つ.
★ ボイルの法則
$p_{1}V_{1}=p_{0}V_{0}$
$\eqalign{V_{1}&=\dfrac{p_{0}}{p_{1}}V_{0}\\&=\dfrac{p+\dfrac{M+m}{S}g}{p+\dfrac{mg}{S}}V_{0}\\&=\dfrac{pS+(M+m)g}{pS+mg}V_{0}}$
したがって,$V_{1}=\dfrac{pS+(M+m)g}{pS+mg}V_{0}$
(3)

気体がした仕事を求めるために$pV$グラフをかくと次のようになるね.
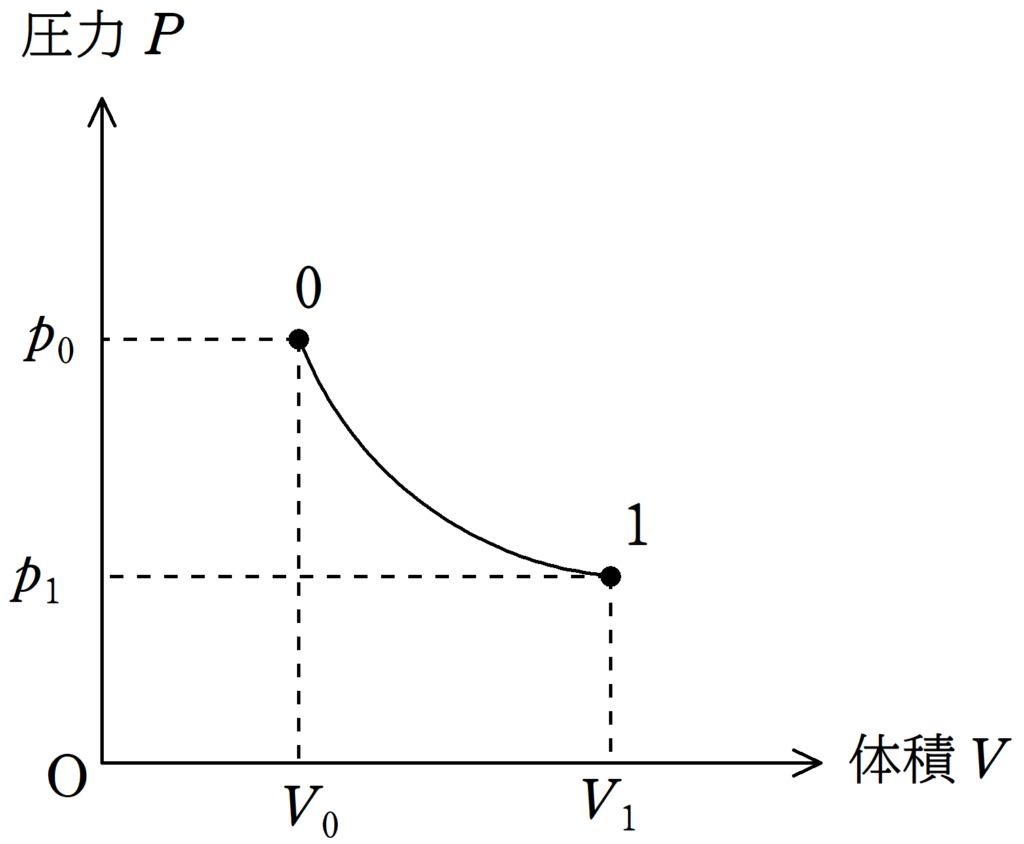

でも,いつものように,曲線と$V$軸で囲まれた面積を求めようとすると大変です.
そこで,今回は$pV$グラフではなく,熱力学第一法則を利用しましょう.
内部エネルギーの変化を$\Delta U$,気体が吸収する熱量を$Q$,気体がした仕事を$W$とすると
$Q=\Delta U+W$

熱量$Q$は問題で与えられているのでよいですが,内部エネルギーの変化がまだわかっていませんね.
しかし,今回は等温変化(つまり,温度変化0$\Delta T=0$)なので,内部エネルギーの変化$\Delta U$は0です.
問題文に単原子分子理想気体とかいてあるときは,次のことを使うことができる.
定積モル比熱が$\dfrac{3}{2}R$である.すなわち
内部エネルギー$U$は
$U=\dfrac{3}{2}nRT=\dfrac{3}{2}pV$
内部エネルギーの変化$\Delta U$は
$\Delta U=\dfrac{3}{2}nR\Delta T=\dfrac{3}{2}(p_{2}V_{2}-p_{1}V{1})$
※$n$:物質量,$T$:絶対温度,$p$:圧力,$V$:体積
★ 熱力学第一法則
$Q=0+W$ $\therefore$ $W=Q$

コメント
[…] […]
[…] […]