
力学的エネルギー保存則は運動量保存則とともに,保存則を立てることができるのかを確認しないといけません.式が成り立たないのに,勝手に立式したのでは×になりますからね.

そうなんだよね...
ただ,2つの物体の問題になると,何が何だかわからなくなるから,簡単にわかる目安がないのかな...

2つの物体での力学的エネルギーが保存する条件は最後にまとめていきたいと思います.
まずは,次の問題をみてください.
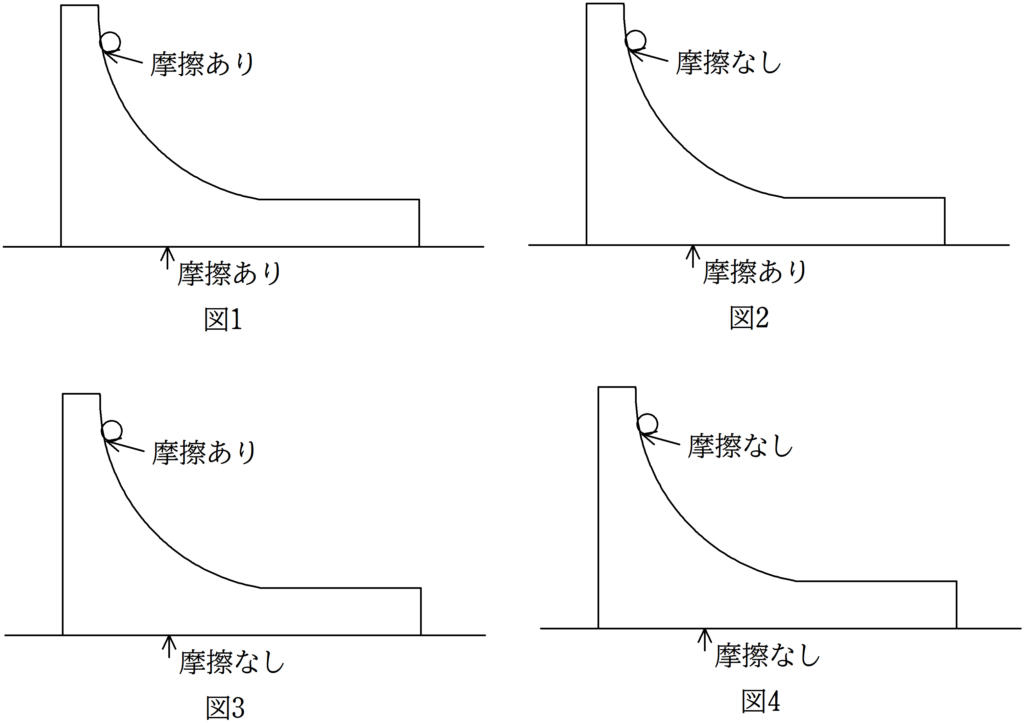
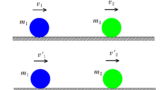
次の図1から図4のように水平な床の上に台と物体がおかれている.
図1は台と床および台と物体の間に摩擦あり,
図2は台と床の間には摩擦があるが,台と物体の間には摩擦なし,
図3は台と床の間には摩擦がないが,台と物体の間には摩擦あり,
図4は台と床および台と物体の間に摩擦なしである.
(1) 図1から図4のうち,物体と台を対象とした水平方向の運動量保存則が成り立つものをすべて選べ.
(2) 図1から図4のうち,物体と台を対象とした力学的エネルギー保存則が成り立つものをすべて選べ.
<解答>
(1) 図3と図4 (2) 図4

運動量が保存する条件はこの記事を読んでみてね.
物体系の水平方向の力の和が0である図を選べばいいから図3と図4なんだね.

運動量保存則と力学的エネルギー保存則は似たような式かと思っていたけど,力学的エネルギーが保存するのは図4だけなんだね・・・

そうなんです.
だから,式が使える条件はきちんと確認しておかなければなりません
.
力学的エネルギー保存則が成り立つ条件

力学的エネルギー保存則が成り立つ条件は
物体系にはたらく非保存力がする仕事が0
です.
運動量保存則のように,力の和が0ではありません.
力学的エネルギー保存則については,こちらの記事を読んでみてください.

ということは,重力や弾性力のような保存力は仕事をしてもいいだね.
あと,力がはたらいても,仕事をしなければ,力学的エネルギーは保存するんだ!

そういうことです.
仕事についての詳しい話は,こちらの記事にかかれています.
垂直抗力がする仕事の和が0!?

図1から図4において,物体と台の間にはたらく垂直抗力がする仕事の和は0です.
まず,このことから確かめていきましょう.
この部分は今回の話で一番大事なところです.

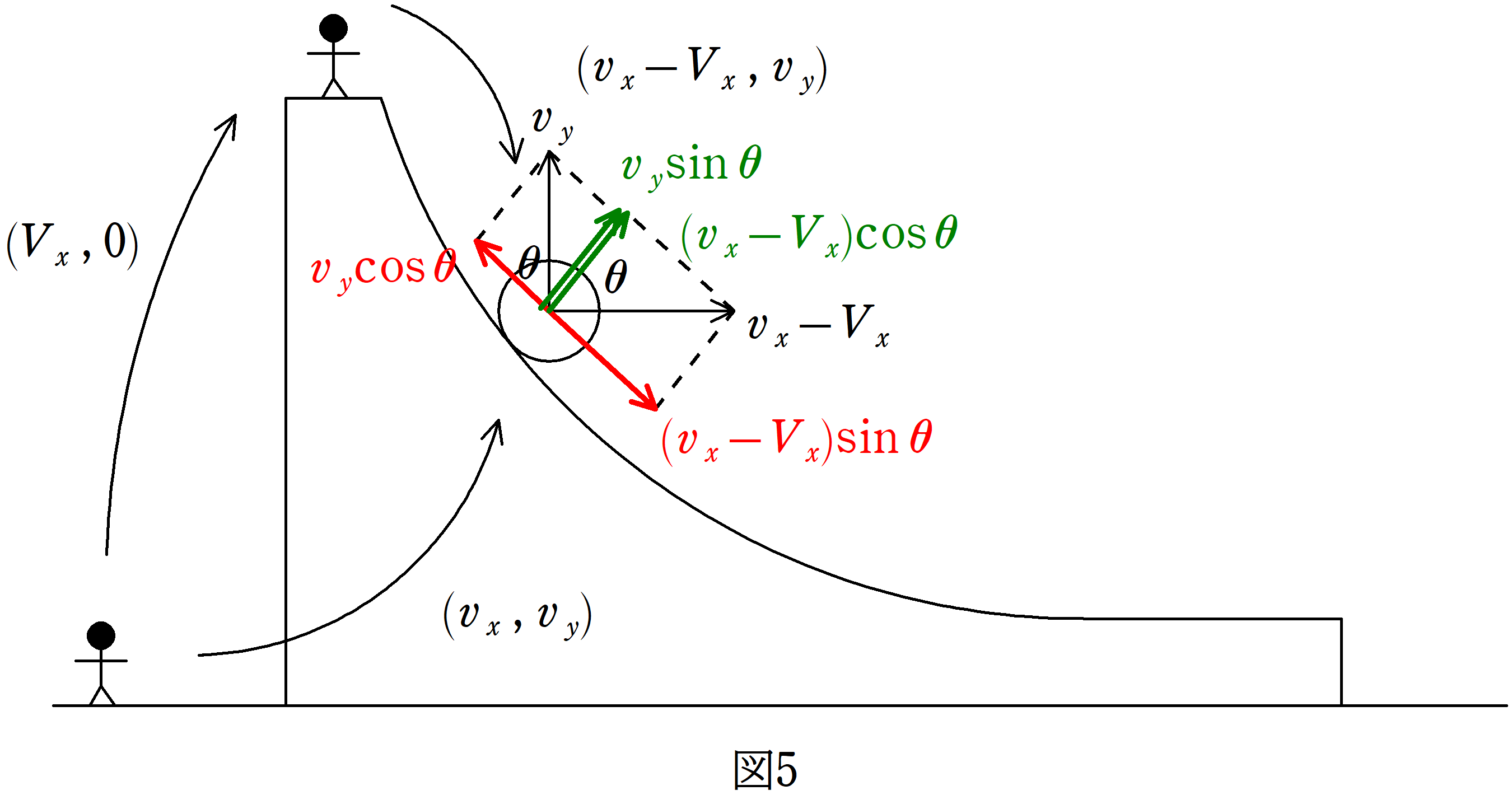
速度の設定をします.
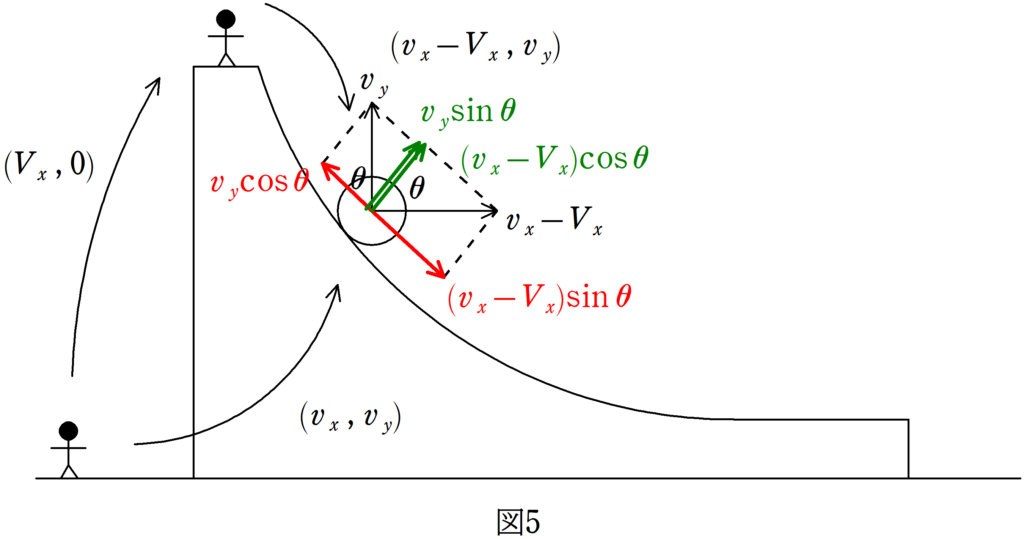
図5の右方向を$x$軸の正の方向,上方向を$y$軸の正方向とします.
物体は2次元運動をしているので,速度ベクトルを$\displaystyle{v_{x} \choose v_{y}}$とします.
また,台の速度は$\displaystyle{V_{x} \choose 0}$とします.
台の速度の$y$方向は速度をもっていないため$0$となっています.

すると,台からみた物体の速度はどうなるでしょうか?
台からみた物体の速度を$\displaystyle{\clubsuit \choose \spadesuit}$とすると,次の式が成り立ちます.
$\displaystyle {v_{x} \choose v_{y}}= {V_{x} \choose 0}+{\clubsuit \choose \spadesuit}$
$\therefore$$\displaystyle{\clubsuit \choose \spadesuit}={v_{x} \choose v_{y}}-{V_{x} \choose 0}={v_{x}-V_{x} \choose v_{y} }$

相対運動の計算だね.
こちらの記事も取り上げているよ.

さらに,この速度を台からみたときの曲面の接線方向成分とそれに対して垂直な成分に分けましょう.
なぜ,このような方向に分けるのかというと,束縛条件を考えたいからです.

台からみたら物体は台に張り付いているので,曲面の接線方向に垂直な方向の速度は0だね.
速度が0という特別な条件がつかえるんだ!

そこで,図5のように,曲面の接線方向に垂直な方向から$x$軸の正方向へのなす角を$\theta$とします.
すると,曲面の接線方向の成分(図5の赤色の速度成分)とそれに対して垂直な速度成分(図5の緑色の速度成分)が出てきます.
束縛条件より,垂直な方向(緑色の速度成分)の速度は0であるので,
$(v_{x}-V_{x})\cos \theta +v_{y}\sin \theta =0$ $\dots (\ast)$

なんのために出した式なの?と思うかもしれませんが,あとで使います.
さて,次に物体と台の間にはたらく垂直抗力の仕事の和について調べます.
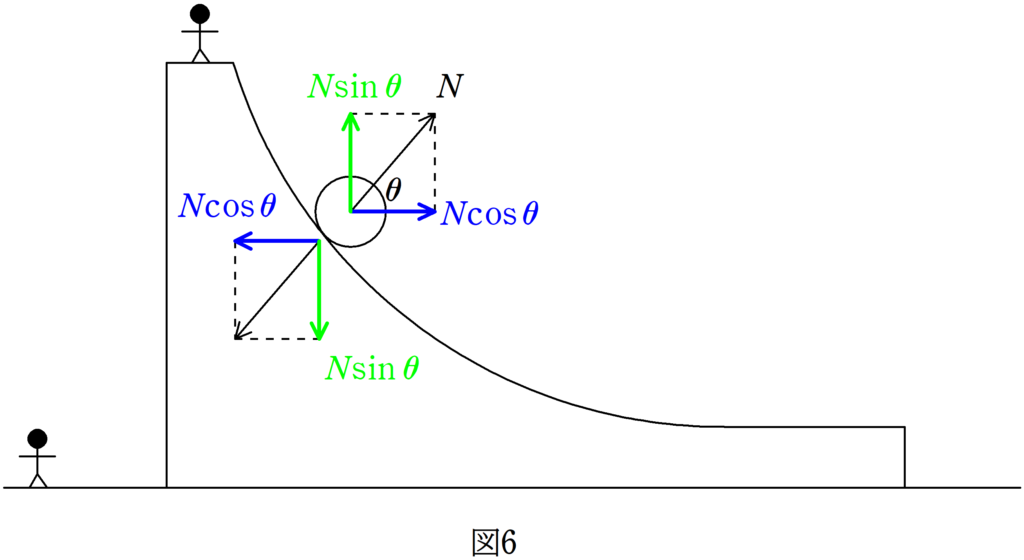

垂直抗力の力の大きさを$N$とします.
この垂直抗力を$x$方向と$y$方向に分けます.
物体の速度は$\displaystyle{v_{x} \choose v_{y}}$であったので,微小な時間$\Delta t$の間に物体にはたらく垂直抗力がする仕事$w$は次のようになります.
$w=N\cos \theta \cdot v_{x}\varDelta t+N\sin \theta \cdot v_{y}\varDelta t$ $\dots (2\ast)$

次に台にはたらく垂直抗力がする仕事$W$を求めます.
台の速度が$\displaystyle{V_{x} \choose 0}$であることから,次のようになります.
$W=-N\cos \theta \cdot V_{x}\varDelta t +(-N\sin \theta)\cdot 0\cdot \varDelta t=-N\cos \theta \cdot V_{x}\varDelta t$ $\dots (3\ast)$
$(2\ast)$と$(3\ast)$から,物体と台の間にはたらく垂直抗力がした仕事の和$w+W$は
$\eqalign{w+W &= N\{v_{x}\cos \theta +v_{y}\sin \theta -V_{x}\cos \theta\}\varDelta t \\&=N\{(v_{x}-V_{x})\cos \theta +v_{y}\sin \theta\}\varDelta t \\&= 0}$

最後の式変形には$(\ast)$の
$(v_{x}-V_{x})\cos \theta +v_{y}\sin \theta =0$
を使いました.
ここで束縛条件が役立つのです.
このようにして,物体と台の間にはたらく垂直抗力がする仕事の和が0であることが示されました.
摩擦力がした仕事の和が0は成り立つ?

垂直抗力は作用反作用の関係だから,結局仕事の和が0になったんじゃないの??

いえ,そういうわけではありません.
次に摩擦力がする仕事をみてみましょう.
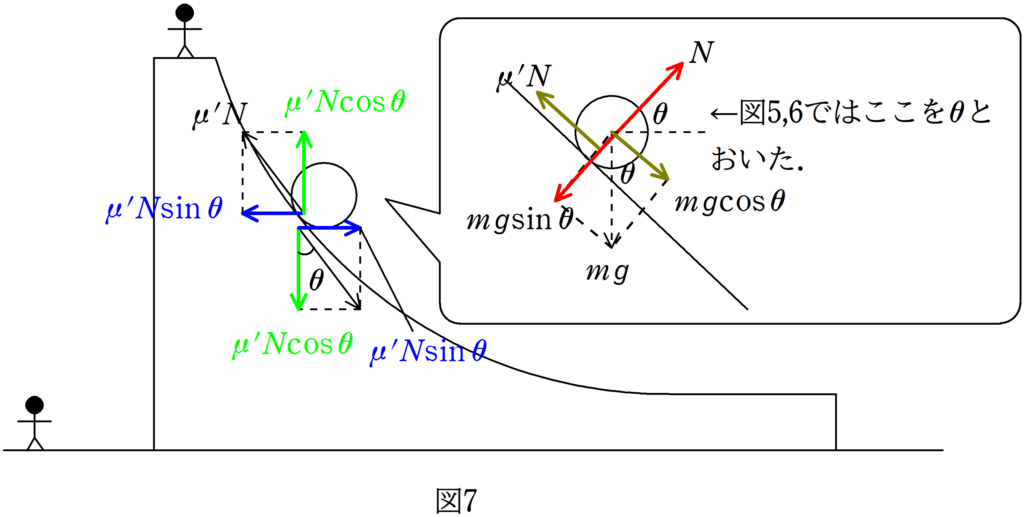

曲面の接線方向に垂直な方向と$x$軸の正方向のなす角を$\theta$とするとき,図7の吹き出し部分のように,曲面に対して垂直な方向のつり合いの式から
$N=mg\sin \theta$

また,曲面と物体の間の動摩擦係数を$\mu^{\prime}$とすると,動摩擦力の大きさは
$\mu^{\prime}N=\mu^{\prime}mg\sin \theta$

となります.
これを図7のように,$x$軸方向と$y$軸方向に分解して動摩擦力がした仕事を計算してみましょう.
物体と台の速度が$\displaystyle{v_{x} \choose v_{y}}$と$\displaystyle{V_{x} \choose 0}$なので,動摩擦力がした仕事の和$W^{\prime}$は,次のようになります.
$\eqalign{W^{\prime}&= -\mu^{\prime}N\sin \theta \cdot v_{x}\varDelta t+\mu^{\prime}N\cos \theta \cdot v_{y}\varDelta t+\mu^{\prime}N\sin \theta \cdot V_{x}\varDelta t+\mu^{\prime}N\cos \theta \cdot 0 \cdot \varDelta t\\&= -\mu^{\prime} N\{(v_{x}-V_{x})\sin \theta -v_{y}\cos \theta \}\varDelta t \\ &\neq 0}$

最後に$\neq$となっている理由は図5の赤色の速度成分(台からみた物体の曲面の接線方向成分)が0でないからです.
やはり摩擦力がした仕事の和は0ではありませんでした.だから図1~図3は力学的エネルギーが保存しないんです.

なるほど,,単純にはいかないのか・・・
もう少し一般化する

2つの物体が動く問題において,作用反作用の力の仕事の和が$0$になるか,ならないのかを調べるのに,次のように一般化することもできます.
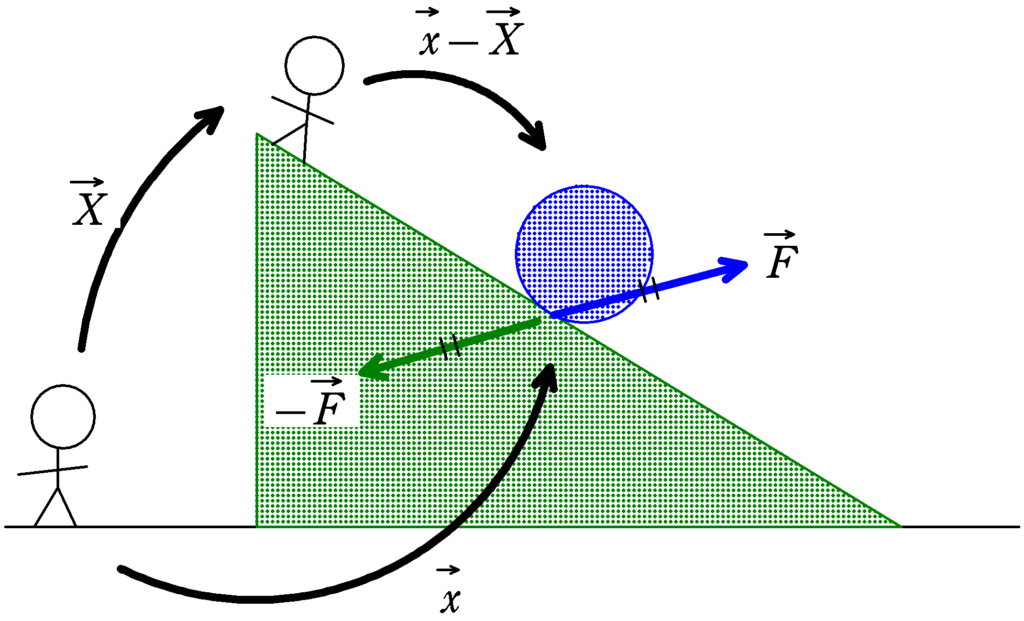

青の物体にはたらく力を$\overrightarrow{F}$とすると,緑にはたらく反作用は$-\overrightarrow{F}$になります.静止している人からみた青の物体と緑の物体の変位をそれぞれ$\overrightarrow{x},\overrightarrow{X}$とすると,青の仕事と緑の仕事$w,W$はそれぞれ次のようになります.
$w=\overrightarrow{F}\cdot \overrightarrow{x}$, $W=-\overrightarrow{F}\cdot \overrightarrow{X}$
仕事の和は
$\eqalign{w+W&=\overrightarrow{F}\cdot \overrightarrow{x}-\overrightarrow{F}\cdot \overrightarrow{X}\\&=\overrightarrow{F}\cdot (\overrightarrow{x}-\overrightarrow{X})}$

$\overrightarrow{x}-\overrightarrow{X}$は,緑からみた青の変位だね.
ということは,作用反作用の力の仕事の和が$0$になるのは,次の2通りあるのかな.
- $\overrightarrow{x}-\overrightarrow{X}=\vec{0}$,つまり2つの物体は一体となって運動しているとき.
- $\overrightarrow{F}$と$\overrightarrow{x}-\overrightarrow{X}$が垂直な関係のとき.つまり,緑からみた(青からみてもよい)青の物体にはたらく力が動く方向と垂直になるとき.
もう1つの類題

それでは,次の問題において,力学的エネルギーが保存するかしないかをチェックしてみましょう.
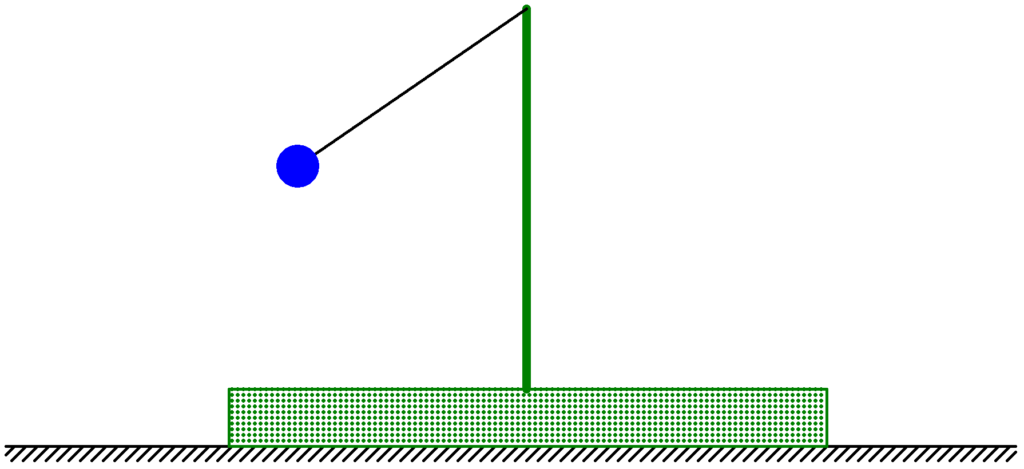
図のように,水平な床の上に台がおかれており,台の上には棒が固定されている.棒には軽くて伸びないひもがつながれており,ひもの他端には小球がつながれている.台と小球を静止した状態でひもを張った状態で小球をもちあげ,台と小球の固定を静かにはずしたところ,運動をはじめた.台は床から離れなかったものとする.摩擦や空気抵抗は無視するとき,台と小球を合わせた対象物体は力学的エネルギーが保存するかしないか.ただし,観測者は床で静止した人である.
<解答>
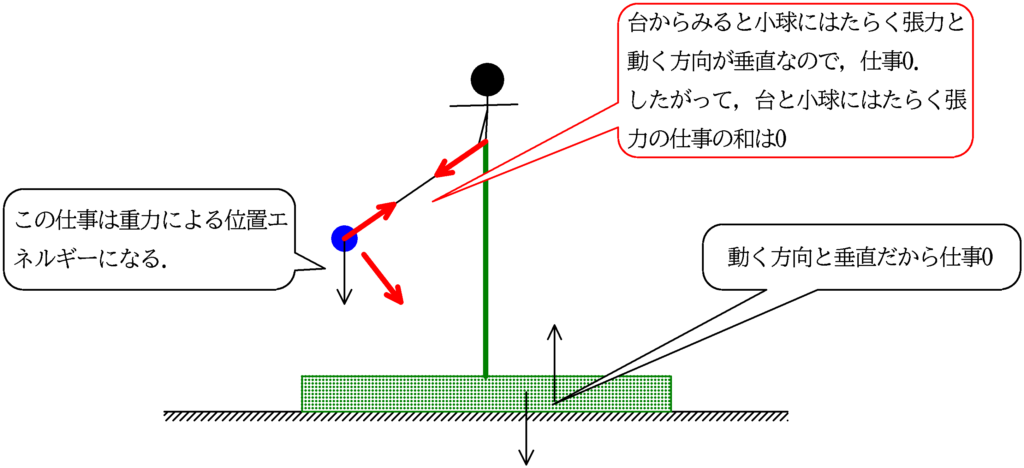

一番怪しい張力は上図の理由から仕事の和が$0$なんだね!
ただし,小球にはたらく張力単体だと仕事は$0$にならないから,小球のみの力学的エネルギーは保存しないよ.
今回は小球と台全体の力学的エネルギーなので,保存します.(答)
まとめ
今までの考察から次のようなことが予想できます.
2つの物体が動くときの力学的エネルギーが保存する条件は,次の2つを同時にみたすときである.
- 物体系外からはたらく非保存力が仕事をしない
- 物体系の間に力がはたらく場合は,片一方の物体からもう片一方の物体を見たときにその力が仕事をしていないとき(今回の例では,台から物体を見ると,垂直抗力はつねに面に対して垂直な方向に力がはたらいているため,仕事をしていないが,摩擦力は面の接線方向に力がはたらいているため,仕事をしている)
実際の問題では,摩擦力がはたらくと,摩擦熱になってしまうから力学的エネルギーが保存しないと考えてもよいですが,束縛条件の考え方自体はとても大事なので,よく理解しておきましょう.



コメント
[…] [二物体の運動]力学的エネルギー保存則が成り立つ条件 […]
[…] […]
束縛条件の部分なのですが、多分符号が逆になっていると思います。違ったらすみません!
本当ですね..ありがとうございます!
訂正します.
台の水平な部分と小球の間に摩擦は働きますか?そうであれば、図3は運動量保存則は成り立たないと思いますが。
「台の上部の水平な部分と小球の間」に摩擦力ははたらきます.
摩擦力がはたらいても,作用反作用の関係のため,水平方向の力の和は0となり,台と小球を物体系とした水平方向の運動量は保存します.
仕事の公式はfxcosθなのにfvcosθとなっていて違うと思います。
この場合単位も違うことになるので速度使ったらダメなのでは?
ご指摘ありがとうございました。
修正いたしました。
小球のベクトルが上向きにVyになっていますが、小球は滑り落ちているのであれば、右下に運動ベクトルがあり、垂直方向(y軸ベクトル)は、上を正にするなら、-Vyになるのではないのでしょうか?
コメントありがとうございます.
$v_{y}$は「速度成分の大きさ」ではなく,「速度成分」として設定しました.
つまり,$(v_{x},v_{y})=(3,-1)$のように$v_{x},v_{y}$自体が正負両方とれる形にしています.
似たような例として,なめからな水平面上において,Aが静止していて,左方向からBがAにぶつかる運動を考える際,Bの衝突後の速度を$V_{\rm B}$とおくのと同じです.
運動量保存則やはね返り係数の式を解くことによって,$V_{\rm B}$が正なのか負なのかがわかります.