
引き続き電荷保存則の演習です.
前回は,「電荷保存則」と「キルヒホッフ則」を立式して解きました.
しかし,コンデンサーが多い場合,キルヒホッフ則で電荷の式を解くのは相当計算が面倒になります.
そこで,今回は電位の設定による解法を使っていく練習をしていきたいと思います..
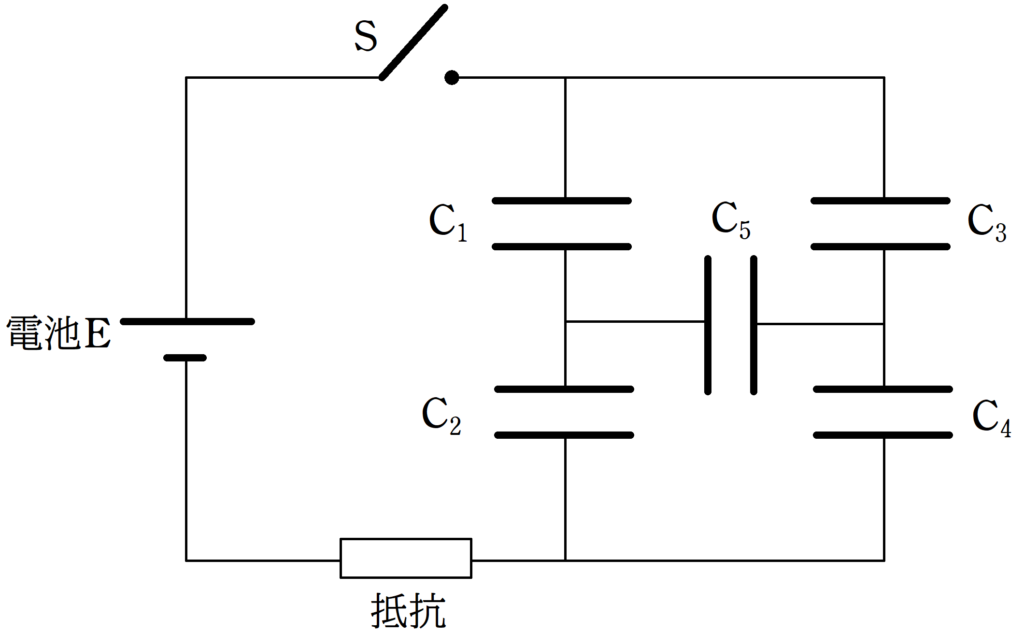
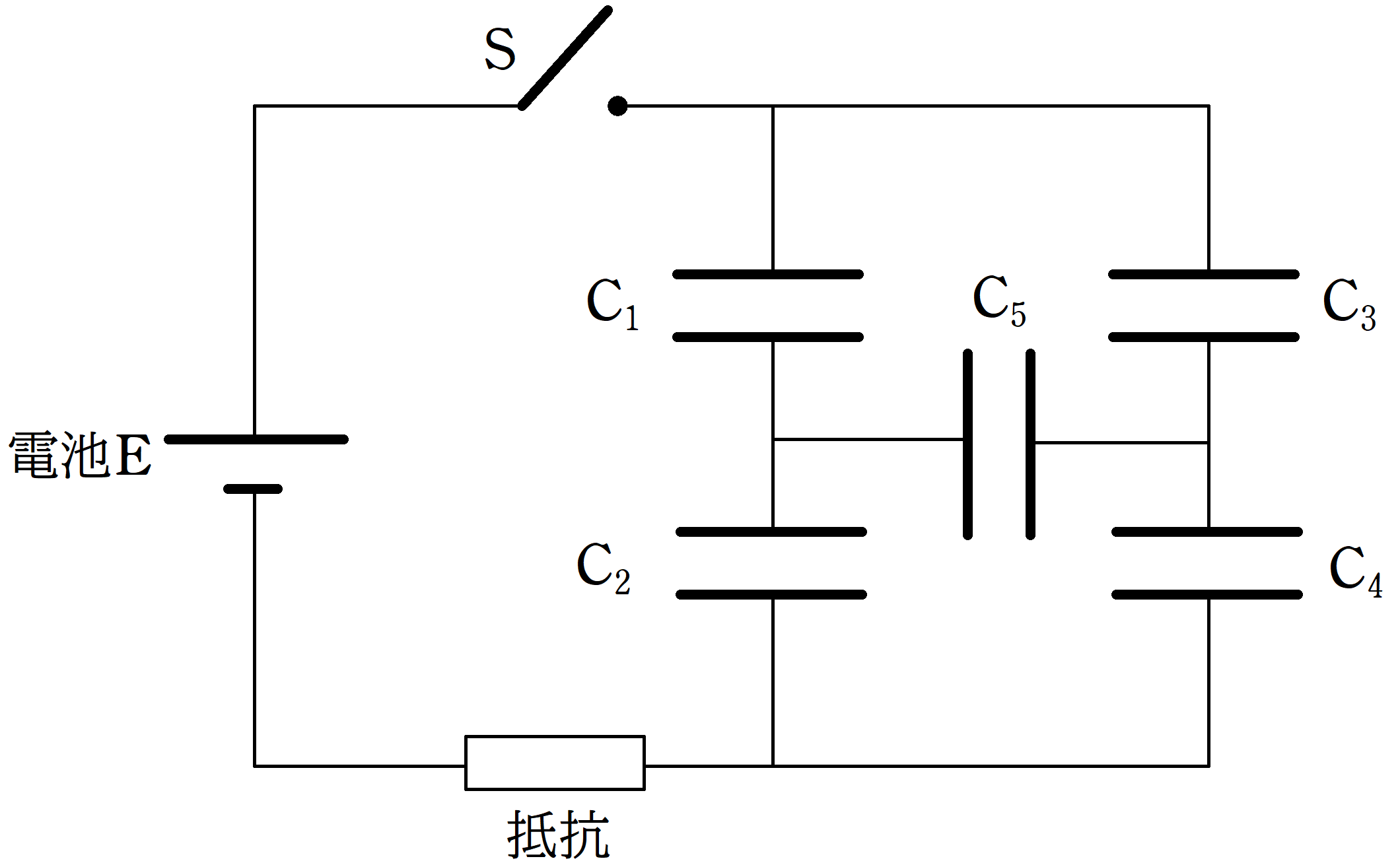
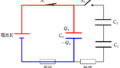
起電力$V$の電池,スイッチと抵抗と5つのコンデンサーによって上図のような回路がつくられている.
コンデンサー$\rm C_{1}$,$\rm C_{2}$,$\rm C_{3}$,$\rm C_{4}$,$\rm C_{5}$の電気容量はそれぞれ,$C$,$2C$,$2C$,$C$,$3C$である.
はじめ,すべてのコンデンサーには電荷が蓄えられていない状態でスイッチを閉じて十分時間が経つと,コンデンサーに電荷が蓄えられた.
コンデンサー$\rm C_{1}$,$\rm C_{2}$,$\rm C_{3}$,$\rm C_{4}$,$\rm C_{5}$に蓄えられた電荷をそれぞれ求めよ.
<解答>
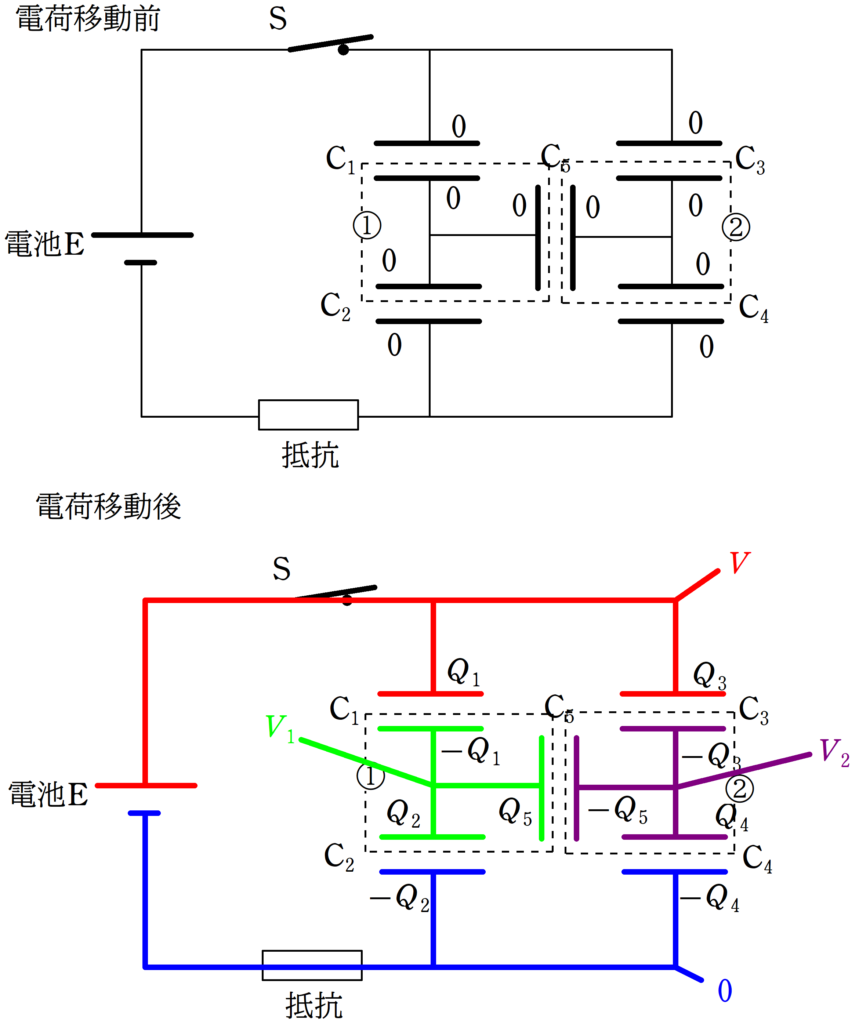

電荷移動後の電荷と電位を上図のように設定します.
立てる式は次の2種類です.
1.①部分と②部分の電荷保存則
2.各コンデンサーのコンデンサーの式
★ 電荷保存則
①の電荷保存則
$-Q_{1}+Q_{2}+Q_{5}=0$
$Q_{1}=Q_{2}+Q_{5}$ $\dots (\ast)$
②の電荷保存則
$-Q_{3}+Q_{4}-Q_{5}=0$
$Q_{3}+Q_{5}=Q_{4}$ $\dots (2\ast)$
★ 各コンデンサーの式
$Q_{1}=C(V-V_{1})$ $\dots (\spadesuit)$
$Q_{2}=2C(V_{1}-0)$ $\dots (2\spadesuit)$
$Q_{3}=2C(V-V_{2})$ $\dots (3\spadesuit)$
$Q_{4}=C(V_{2}-0)$ $\dots (4\spadesuit)$
$Q_{5}=3C(V_{1}-V_{2})$ $\dots (5\spadesuit)$
$(\spadesuit)$~$(5\spadesuit)$を$(\ast)$と$(2\ast)$に代入し,$V_{1}$と$V_{2}$を求める.
★ $(\ast)$に代入
$C(V-V_{1})=2CV_{1}+3C(V_{1}-V_{2})$
$\therefore 6V_{1}-3V_{2}=V$ $\dots (\heartsuit)$
★ $(2\ast)$に代入
$2C(V-V_{2})+3C(V_{1}-V_{2})=CV_{2}$
$\therefore -3V_{1}+6V_{2}=2V$ $\dots (2\heartsuit)$
$(\heartsuit)$と$(2\heartsuit)$を解いて,
$V_{1}=\dfrac{4}{9}V$,$V_{2}=\dfrac{5}{9}V$
これらを$(\spadesuit)$~$(5\spadesuit)$に代入して
$Q_{1}=C(V-\dfrac{4}{9}V)=\dfrac{5}{9}CV$
$Q_{2}=2C(\dfrac{4}{9}V-0)=\dfrac{8}{9}CV$
$Q_{3}=2C(V-\dfrac{5}{9}V)=\dfrac{8}{9}CV$
$Q_{4}=C\cdot (\dfrac{5}{9}V-0)=\dfrac{5}{9}CV$
$Q_{5}=3C(\dfrac{4}{9}V-\dfrac{5}{9}V)=-\dfrac{1}{3}CV$

$Q_{5}<0$ということは,$\rm C_{5}$の電荷の設定が逆だったってことだね.
一見,たくさん式があるように見えるけど,実質$V_{1}$と$V_{2}$の連立方程式にもっていけるから,なんとか解けそう!
したがって,$\rm C_{1}$から$\rm C_{5}$に蓄えれた電荷は,順に
$\dfrac{5}{9}CV$,$\dfrac{8}{9}CV$,$\dfrac{8}{9}CV$,$\dfrac{5}{9}CV$,$\dfrac{1}{3}CV$


コメント
[…] 電荷保存則演習2 電位の設定による解法PHYさん引き続き電荷保存則の演習… […]
[…] 電荷保存則演習2 電位の設定による解法PHYさん引き続き電荷保存則の演習… […]