回折格子演習1 | Physicmath（フィジクマス）

問題

上図のように，格子定数$d$の回折格子がある．

この回折格子に波長$\lambda$の単色光の平行光線を垂直に当てたところ，スクリーン上に明線ができた．

上図は光を当てた方向から角度$\theta$の方向に明線ができたときの様子を表している．

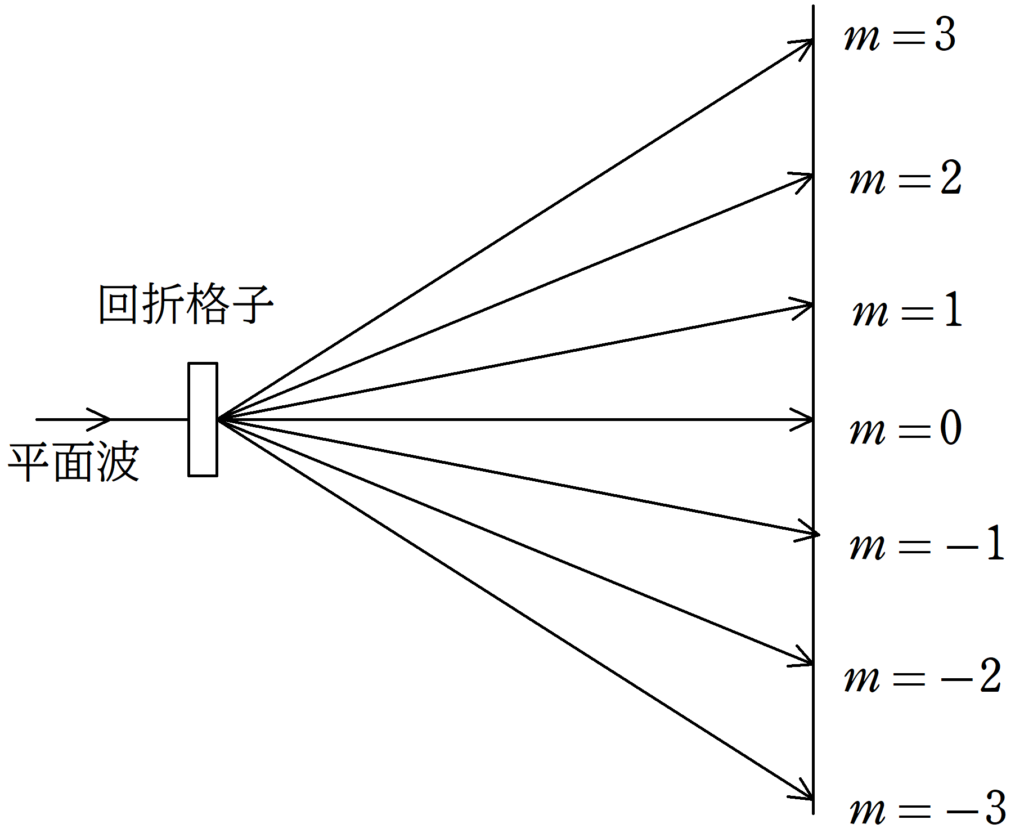
上図（明線の位置は等間隔に見えるが，実際は等間隔ではない．）のようにスクリーンには7本の明線ができたとき，次の問いに答えよ．

(1)　角度$\theta(0<\theta<\dfrac{\pi}{2})$の方向に明線ができる条件を$d$，$\lambda$，$\theta$，整数$m$を用いて表せ．

(2)　スクリーンに明線が7本観測できたとき，$d$と$\lambda$の間に成り立つ不等式をかけ．

＜解答＞

(1)　

NEKO

明線ができるには，隣り合う光線の位相（振動のタイミング）が合えばよいね．

位相が合うには，隣り合う光線の経路差の中にちょうど1個分，2個分，3個分，・・・，というように，整数個分の波があればタイミングがあって，明線ができます．

波の数

波の波長を$\lambda$（波1個分の長さ），波の個数を$N$，波全体の長さを$\Delta L$とすると，次の関係式が成り立つ．

$\Delta L=N\cdot \lambda$

$\therefore　N=\dfrac{\Delta L}{\lambda}$

NEKO

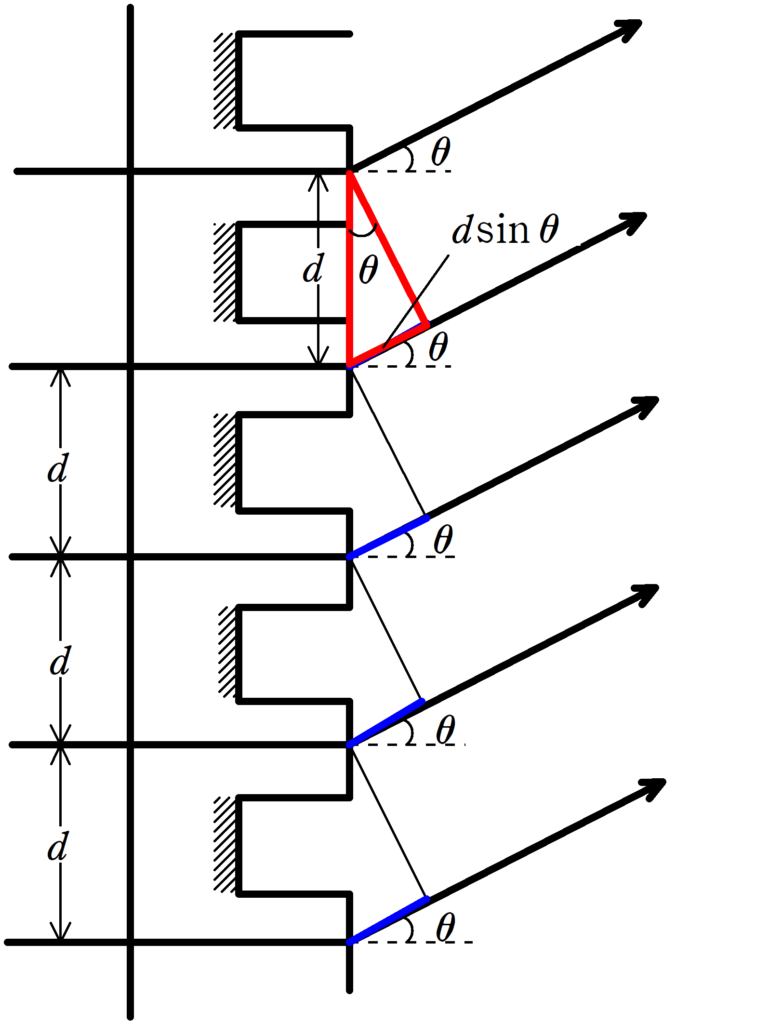
上図のように，隣り合う光線の経路差は$d\sin\theta$となります．

この中に整数個の波があればよいので

★　明線条件

$\dfrac{d\sin\theta}{\lambda}=m$

答えは，$d\sin\theta=m\lambda$

(2)　

NEKO

(1)からわかる通り，$|m|$は波の数を表しています．

NEKO

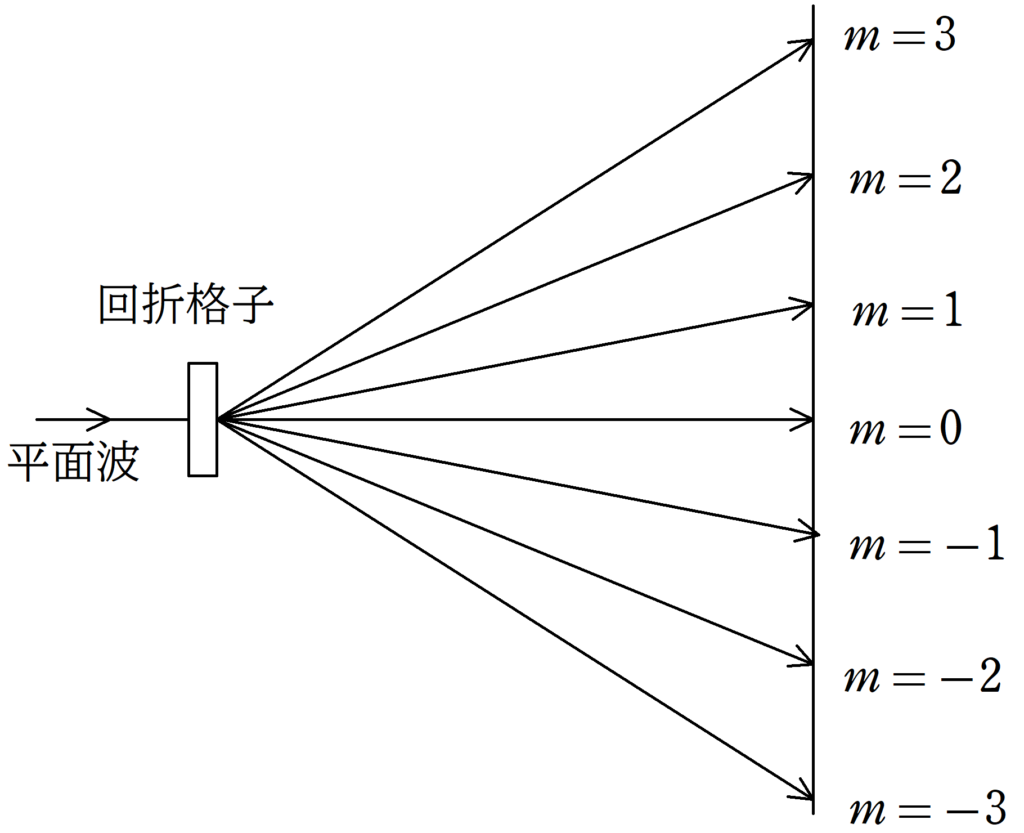
つまり，$m=0$の明線は，波の数の差がない明線です．

$m=1$や$m=-1$は，経路差の中にある波の数が1個であるということを表しています．

$m=2$や$m=-2$は，経路差の中にある波の数が2個であるということを表しています．

$m=3$や$m=-3$は，経路差の中にある波の数が3個であるということを表しています．

さて，経路差の中に入る波の数は永遠に多くなってくでしょうか？

これは，隣り合う光線の距離が$d$であることから，経路差にある波の数は有限であると予想できます．

実際

$d\sin\theta =m\lambda$

$\therefore　\sin\theta=\dfrac{m\lambda}{d}$

を満たす$\theta$は$\sin\theta$が$-1<\sin\theta <1$であることから

$-1<\dfrac{m\lambda}{d}<1$

(ちなみに，$\sin\theta =1，-1$，すなわち$\theta =90°，-90°$の方向にはスクリーンがないので，除きました．）

さらに変形して

$-\dfrac{d}{\lambda}<m<\dfrac{d}{\lambda}$

そこで，$m=3$の明線が生じるが，$m=4$の明線が生じない条件は次のようになります．

$3<\dfrac{d}{\lambda}$　かつ　$\dfrac{d}{\lambda}\leqq 4$

まとめて

$\dfrac{d}{4}\leqq \lambda <\dfrac{d}{3}$　(答)