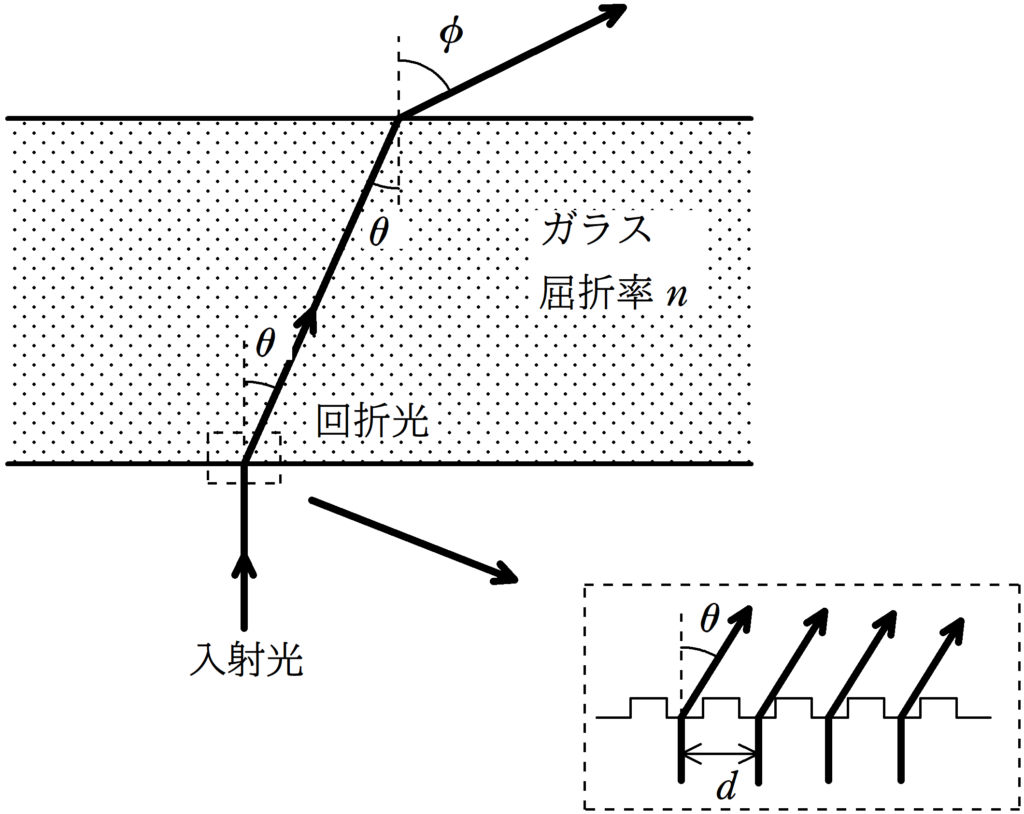
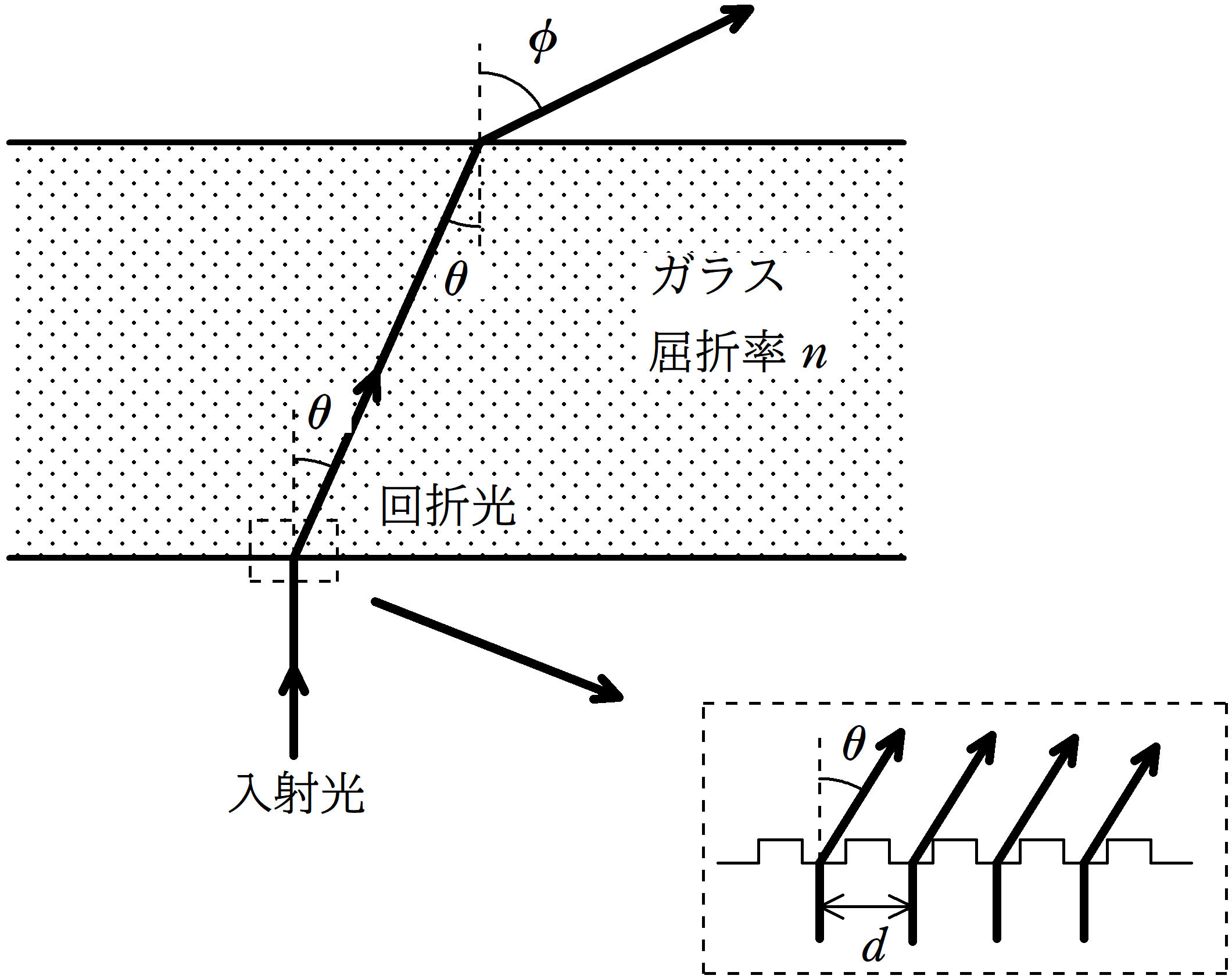
上図のように,屈折率$n$の十分厚いガラス板の下面に,一定の間隔$d[\rm m]$で多数の平行なすじを引いて回折格子をつくった.
上図の矢印のように,波長$\lambda[\rm m]$の単色光の平行光線を下方より,回折格子に垂直に入射させた.
$n=1.5$,$d=1.6×10^{-6} \rm m$,$\lambda=6.0×10^{-7} \rm m$であるときを考える.
回折光がガラスから空気中に出るときに,全反射する可能性があることに注意して,回折格子の上側から観測したときにできる明線の数を答えよ.
<解説>

まずは,明線の条件から考えてみましょう.
回折格子は多数のすじを通る光線のすべての位相が観測点で一致するときに強め合います.
隣り合う光線の経路差は次のようになります.
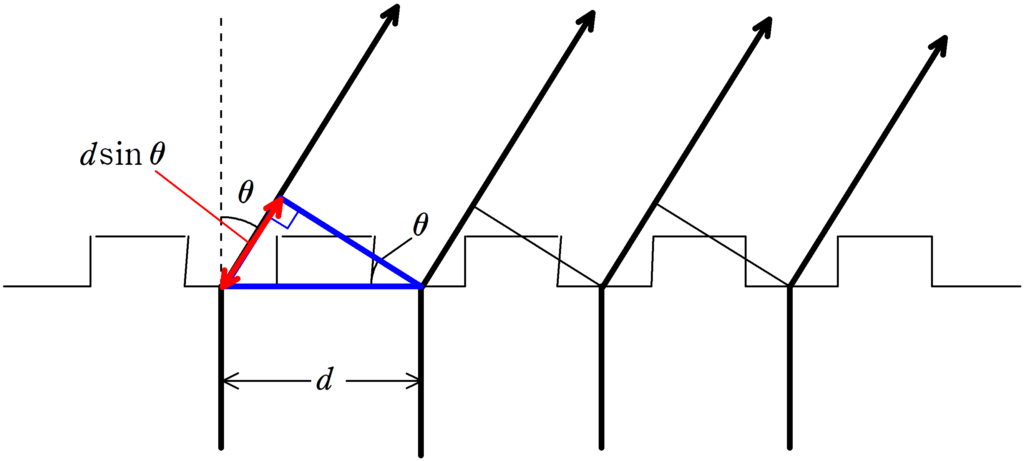

経路差である$d\sin\theta$の中に整数個分の波があれば,位相(タイミング)が合い,光は強め合います.
波の数は次のように数えることを覚えておくとよいでしょう.
波の波長を$\lambda$(波1個分の長さ),波の個数を$N$,波全体の長さを$\Delta L$とすると,次の関係式が成り立つ.
$\Delta L=N\cdot \lambda$
$\therefore N=\dfrac{\Delta L}{\lambda}$

屈折率$n$のガラスに入ったときの波長はもとの$\dfrac{1}{n}$になることに注意です.
★ 経路差にある波の数
経路差の中にある波の数を$N$とする.
$N=\dfrac{d\sin\theta}{\dfrac{\lambda}{n}}=\dfrac{nd\sin\theta}{\lambda}$
★ 明線条件
$m$を整数として
$N=m$
したがって
$\eqalign{\dfrac{nd\sin\theta}{\lambda}&=m\cr \sin\theta &=\dfrac{m\lambda}{nd}}$

この式に,$n=1.5$,$d=1.6×10^{-6} \rm m$,$\lambda=6.0×10^{-7} \rm m$を代入してみましょう.
$\eqalign{\sin\theta&=\dfrac{m\cdot 6.0×10^{-7}}{1.5\cdot 1.6×10^{-6}}\\&=\dfrac{1}{4}m}$ $\dots (\ast)$

$-1<\sin\theta<1$の条件から
$-1<\dfrac{1}{4}m<1$
$-4<m<4$
となり,$m=-3 , -2 , -1 , 0 , 1 , 2 , 3$の計7本の明線が観測できそうです.($m=4 , -4$は観測からはずしました.)
しかし,実際はこれよりもさらに少ない明線しか観測できません.

問題文にも書かれているけど,回折光が空気中にすべてでるわけではないんだね.
全反射しないための条件を考えないとだね.
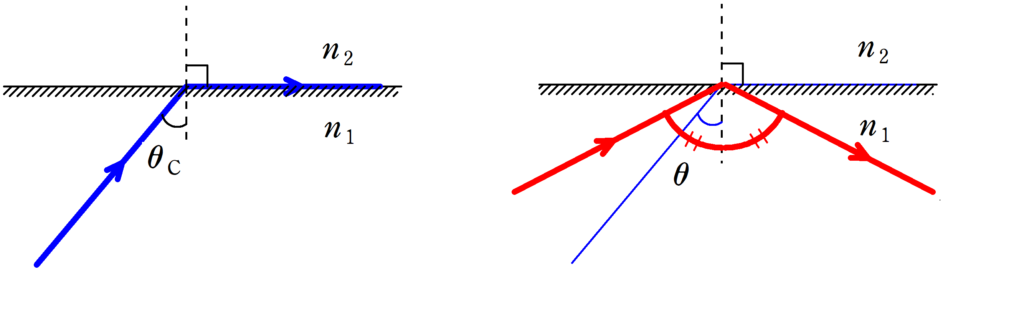
屈折率$n_{1}$の媒質から屈折率$n_{2}$の媒質への波の入射を考える.
屈折角が$90°$に相当するときの入射角を臨界角といい,$\theta_{\rm C}$とする.
臨界角$\theta_{\rm C}$よりも大きい入射角$\theta$で入射すると,波は屈折せず,すべて反射する.これを全反射という.
すなわち,全反射する条件は
$\theta_{\rm C}<\theta$
である.また,臨界角のときの屈折の法則より
$\eqalign{n_{1}\sin\theta_{\rm C}&=n_{2}\sin90°\cr \sin\theta_{\rm C}&=\dfrac{n_{2}}{n_{1}}}$
$0<\sin\theta_{\rm C}<1$より
$\dfrac{n_{2}}{n_{1}}<1$
$\therefore n_{2}<n_{1}$
すなわち,全反射は,屈折率が大きい方から小さい方へ入射するときに起こる.

では,臨界角の計算からしていきましょう.
臨界角を$\theta_{\rm C}$として,屈折の法則の式を立てます.
★ 屈折の法則
$\eqalign{1.5\cdot \sin\theta_{\rm C}&=1\sin90^{\circ}\\ \sin\theta_{\rm C}&=\dfrac{2}{3}}$

じゃあ,全反射しない条件は$\sin\theta<\dfrac{2}{3}$だね.
反対側の光線も考えて
$-\dfrac{2}{3}<\sin\theta<\dfrac{2}{3}$
に$(\ast)$の$\sin\theta=\dfrac{1}{4}m$を代入してみましょう.
★ 明線が観測できる条件
$-\dfrac{2}{3}<\dfrac{1}{4}m<\dfrac{2}{3}$
$\therefore -\dfrac{8}{3}<m<\dfrac{8}{3}$
この不等式を満たす$m$は
$m=-2 , -1 , 0 , 1 , 2 $
したがって,観測できる明線の数は5本

コメント