交流演習　基礎演習1　電圧から電流を求める

PHYさん

今回は，

回路素子にある電圧がわかっているときに，電流を求める

練習をしていきます．

電圧と電流の瞬時値（時刻$t$における電圧，電流）を求める際には，次の2つがわかれば解くことができます．

• 最大値
• 位相

次のことを確認して問題を解いてみましょう．

問題　電圧→電流

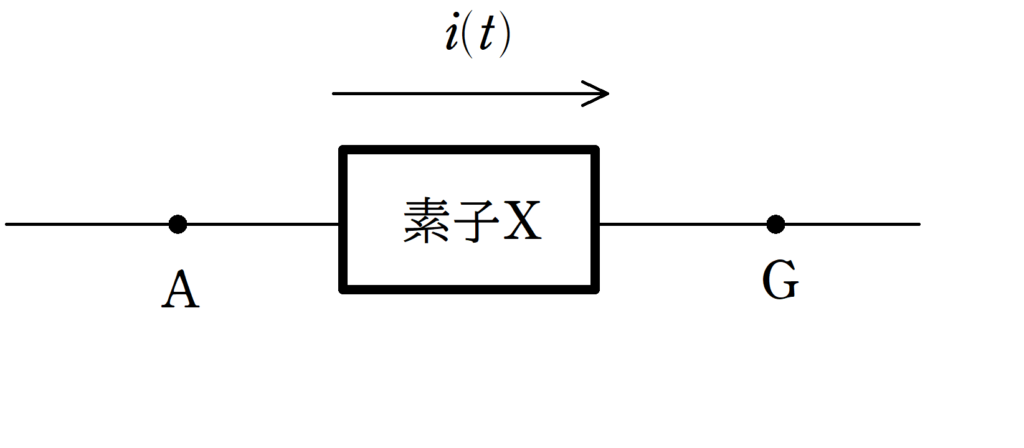
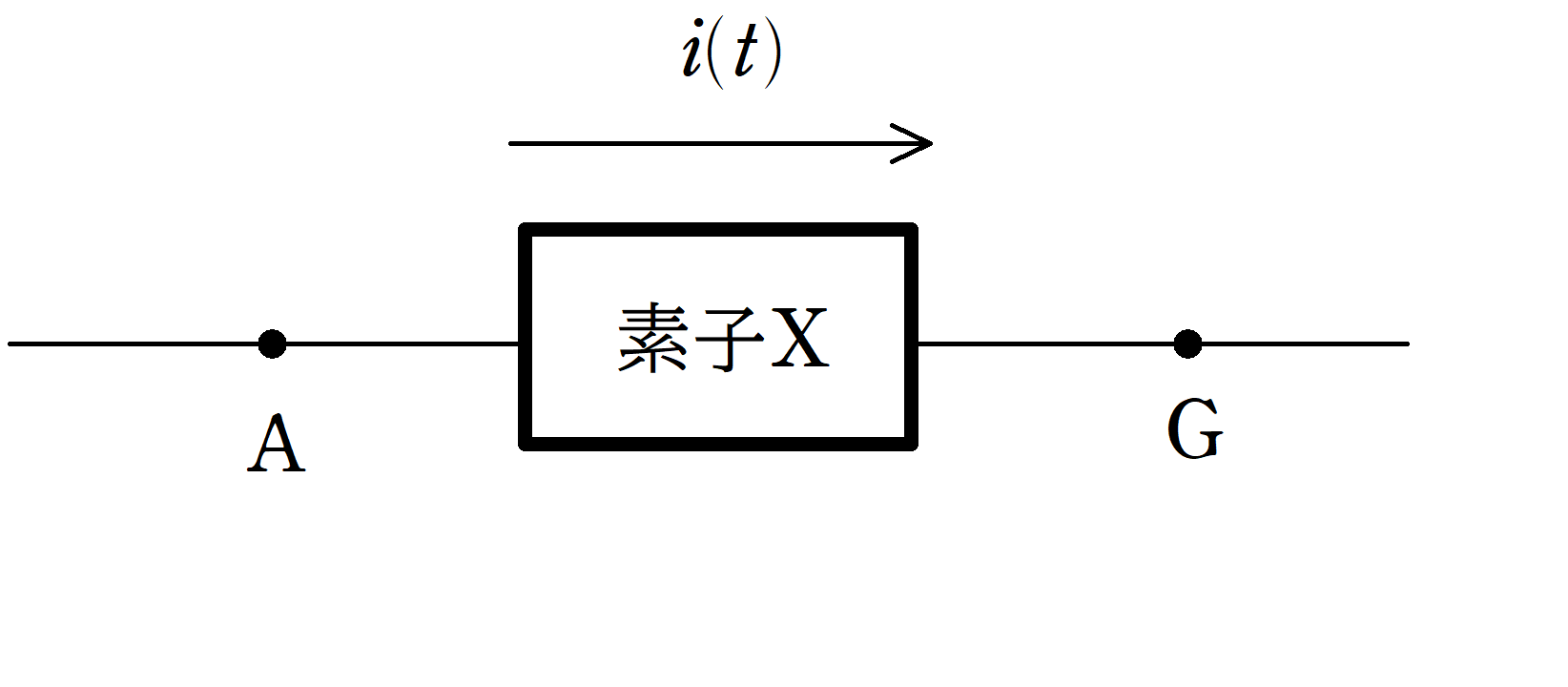
抵抗値$R$の抵抗，電気容量$C$のコンデンサー，自己インダクタンス$L$のコイルについて考える．Gに対するAの電位$V(t)$が次のように与えられたときに，上図の向きに流れる電流の瞬時値$i(t)$を求めよ．ただし，$V_{0}>0$とし，角周波数は$\omega $である．

(1)　素子Xが抵抗で$V(t)=V_{0}\sin\omega t$のとき

(2)　素子Xがコンデンサーで$V(t)=V_{0}\cos\omega t$のとき

(3)　素子Xがコイルで$V(t)=V_{0}\sin\omega t$のとき

(4)　素子Xがコンデンサーで$V(t)=V_{0}\sin\omega t$のとき

(5)　素子Xがコイルで$V(t)=V_{0}\cos \omega t$のとき

(6)　素子Xが抵抗で$V(t)=V_{0}\cos\omega t$のとき

<解答>

(1)　電流の最大値$i_{0}$は

$i_{0}=\dfrac{V_{0}}{R}$

さらに，電圧と電流の位相差はないので

$i(t)=\dfrac{V_{0}}{R}\sin\omega t$　(答)

(2)　電流の最大値$i_{0}$は

$i_{0}=\dfrac{V_{0}}{\dfrac{1}{\omega C}}=\omega CV_{0}$

さらに，電圧（電荷）に対して，電流は位相が$\dfrac{\pi}{2}$進んでいるので

$\eqalign{i(t)&=\omega CV_{0}\cos(\omega t+\dfrac{\pi}{2})\\&=-\omega CV_{0}\sin \omega t}$　(答)

(3)　電流の最大値$i_{0}$は

$i_{0}=\dfrac{V_{0}}{\omega L}$

さらに，電圧に対して，電流は位相が$\dfrac{\pi}{2}$遅れるので

$\eqalign{i(t)&=\dfrac{V_{0}}{\omega L}\sin(\omega t-\dfrac{\pi}{2})\\&=-\dfrac{V_{0}}{\omega L}\cos\omega t}$　(答)

(4)　電流の最大値$i_{0}$は

$i_{0}=\dfrac{V_{0}}{\dfrac{1}{\omega C}}=\omega CV_{0}$

さらに，電圧（電荷）に対して，電流は位相が$\dfrac{\pi}{2}$進んでいるので

$\eqalign{i(t)&=\omega CV_{0}\sin(\omega t+\dfrac{\pi}{2})\\&=\omega CV_{0}\cos \omega t}$　(答)

(5)　電流の最大値$i_{0}$は

$i_{0}=\dfrac{V_{0}}{\omega L}$

さらに，電圧に対して，電流は位相が$\dfrac{\pi}{2}$遅れるので

$\eqalign{i(t)&=\dfrac{V_{0}}{\omega L}\cos(\omega t-\dfrac{\pi}{2})\\&=\dfrac{V_{0}}{\omega L}\sin\omega t}$　(答)

(6)　電流の最大値$i_{0}$は

$i_{0}=\dfrac{V_{0}}{R}$

さらに，電圧と電流の位相差はないので

$i(t)=\dfrac{V_{0}}{R}\cos\omega t$　(答)