[基本]単振動の演習問題① | Physicmath（フィジクマス）

PHYさん

単振動はなんとくなく”周期の公式を覚えておけば大丈夫なのかな？”などのように考えがちですが，そんなことはありません．

単振動は基本の問題と入試レベルの間の問題というものがあまりなく，さらにはかなり多くのことを要求されるので苦手分野になりがちです．

この演習シリーズを通して，一つずつ単振動を解く技術を身に着けていきましょう．

さて，今回の目標は

座標の式$x(t)$を求める座標の式$x(t)$を求める

です．

NEKO

物体がどこにあるかを表す式だね．

PHYさん

座標$x(t)$を求めるためには次のことがわからないといけません．

PHYさｎ

振動を表現するには，

“1.振動の中心”はどこか，

“2.初期位相”どこからスタートするか，

“3.振幅”どれくらいのふり幅で振動するのか，

“4.角振動数，周期”その振動が1周するのにかかる時間，

を把握する必要があります．

しかし，いきなり全部を同時に行うのは大変なので，まずは初期位相から考えてみましょう．

要は$\sin$なのか$\cos$なのか$-\sin$なのか$-\cos$なのかを把握しましょうということです．

もちろん，この他の場合もあるのですが，まずはこの4つのうちのどれかを考えていきましょう．

問題1　初期位相の演習

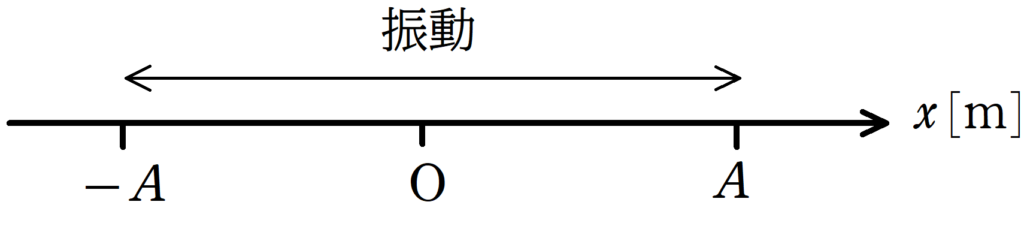
ある物体が原点を中心に$x$軸上を振幅が$A$[$\rm{m}$]，角振動数が$\omega$[$\rm{rad/s}$]で単振動している．

次の運動について，時刻$t$[$\rm{s}$]における位置$x$[$\rm{m}$]の式を答えよ．

(1)　$t=0[\rm{s}]$に$x=A[\rm{m}]$から出発する単振動．

(2)　$t=0[\rm{s}]$に$x=0[\rm{m}]$から$x$軸の正方向に出発する単振動．

(3)　$t=0[\rm{s}]$に$x=0[\rm{m}]$から$x$軸の負方向に出発する単振動．

(4)　$t=0[\rm{s}]$に$x=-A[\rm{m}]$から出発する単振動．

<解答>

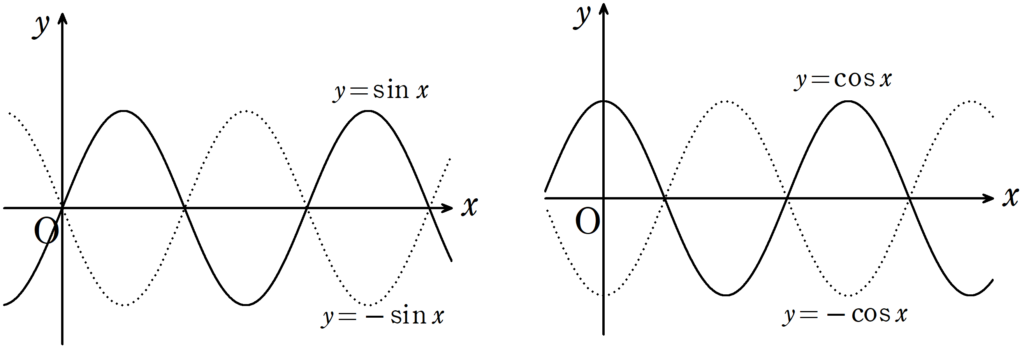
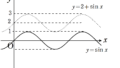
$y=\sin x$，$y=-\sin x$，$y=\cos x$，$y=-\cos x$グラフは上のようになることは覚えておくとよいでしょう．

$y=\sin x$は0から出発して，次の瞬間正の方向に移動し，

$y=-\sin x$は 0 から出発して次の瞬間負の方向に移動します．

$y= \cos x$は最も高いところから次の瞬間負の方向に移動し，

$y=-\cos x$は最も低いところから次の瞬間正の方向に移動します．

今回の振動はこれらの$\sin$型，$-\sin$型，$\cos$型，$-\cos$型のいずれかになるかを判断します．

また，角振動数は$\omega$なので，位相（$\sin , \cos$のなかみ）は$\omega t$，振幅は$A$であることにも注意します．

(1)　最高点から負の方向へ移動しているので$\cos$型．$x=A \cos (\omega t)$

(2)　原点から正の方向へ移動しているので$\sin$型．$x=A \sin (\omega t)$

(3)　原点から負の方向へ移動しているので$-\sin 型$．$x=-A \sin (\omega t)$

(4)　最下点から正の方向へ移動しているので$-\cos$型．$x=-A \cos (\omega t)$

NEKO

数学Ⅱで習う三角関数のグラフが頭に入っていれば難しくないね！

今日はこれでおしまいです！

次回