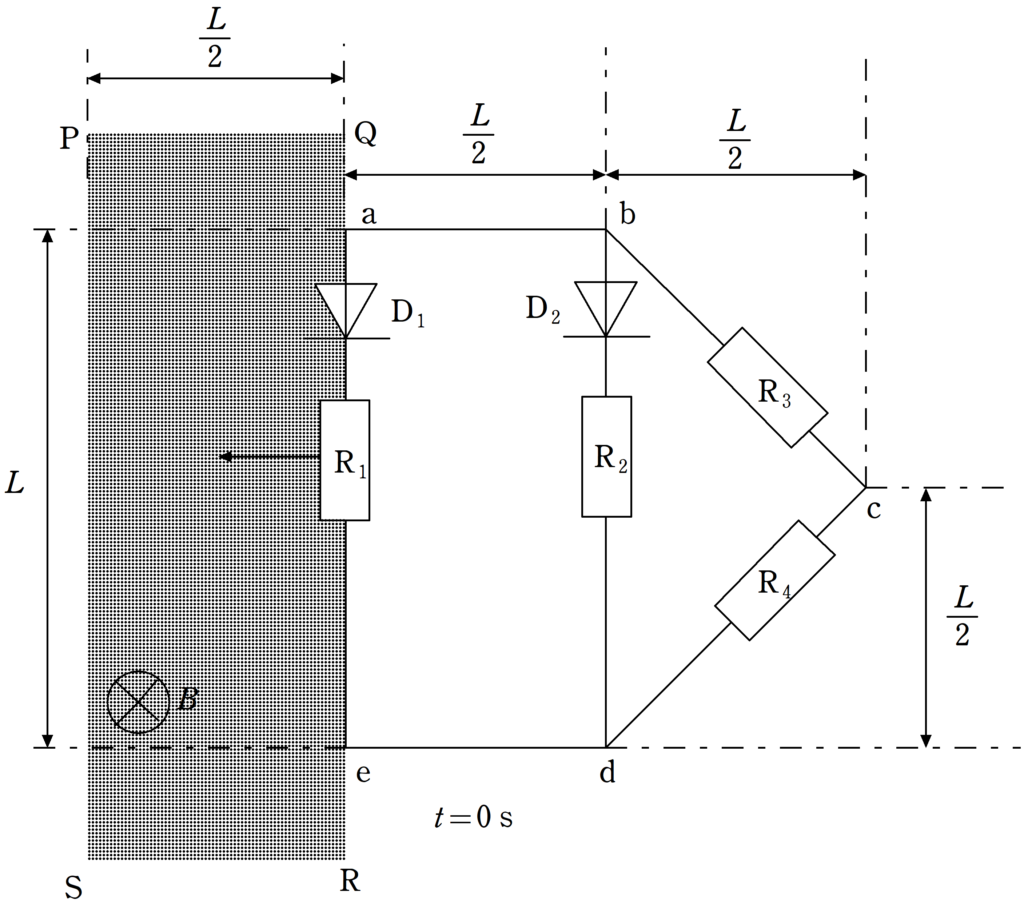
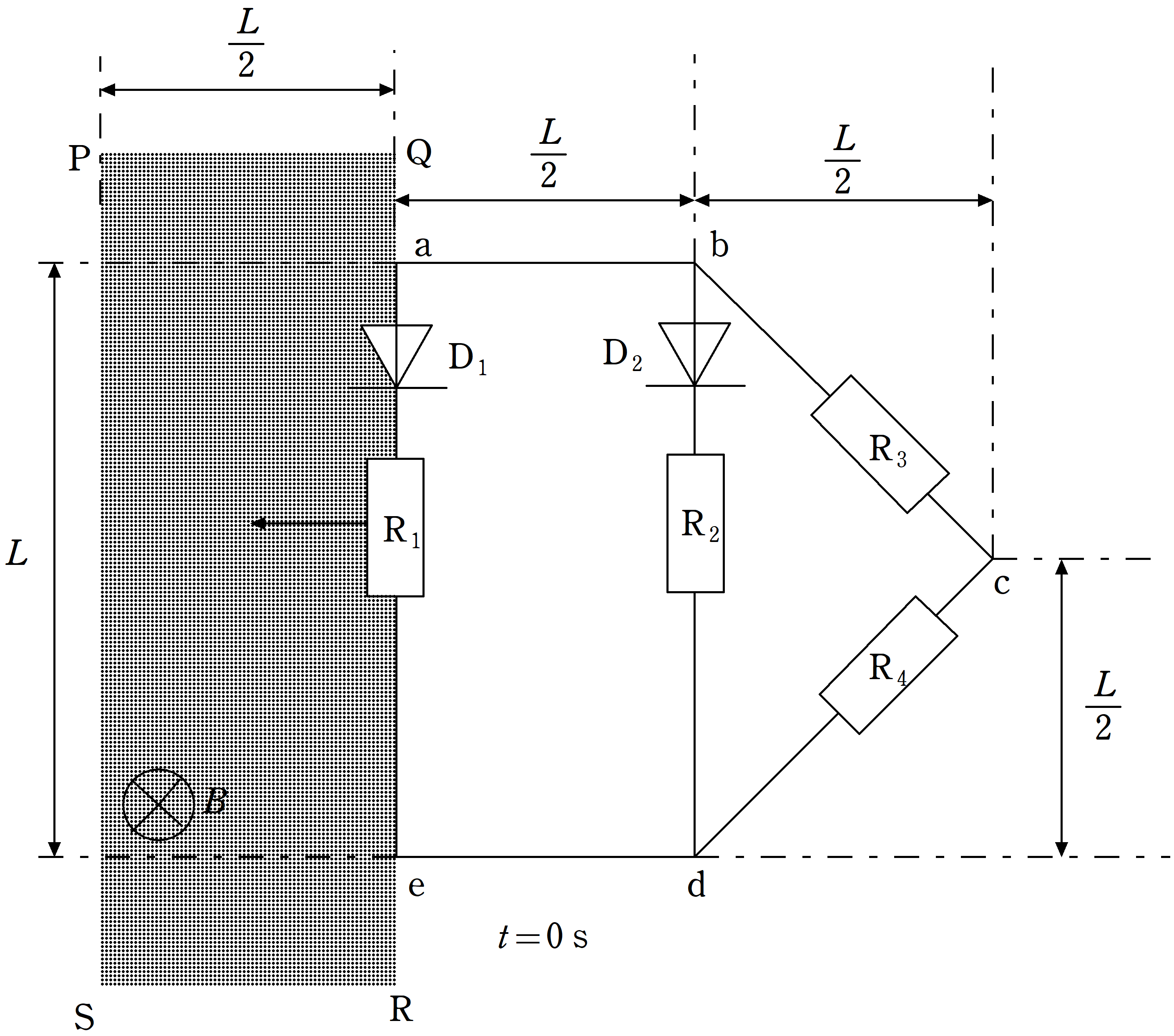
上図のように,抵抗値$R[\Omega]$の抵抗$\rm R_{1}$,$\rm R_{2}$,$\rm R_{3}$,$\rm R_{4}$とダイオード$\rm D_{1}$,$\rm D_{2}$からなる回路があり,回路上の各点に記号$\rm a$,$\rm b$,$\rm c$,$\rm d$,$\rm e$がつけてある.ダイオードは順方向の抵抗がゼロであり,逆方向の抵抗が無限大とみなせるものとする.長方形の回路${\rm abde}$のうち,$\rm ab$間の長さは$\dfrac{L}{2}[\rm m]$であり,$\rm ae$間の長さが$L[\rm m]$である.直角二等辺三角形の回路$\rm bcd$のうち,等辺である$\rm bc$と$\rm cd$の長さが$\dfrac{\sqrt{2}L}{2}[\rm m]$である.上図の網かけで示された長方形$\rm PQRS$の領域に,磁束密度$B[\rm T]$の磁場が紙面に垂直に表から裏の向きに加えられている.回路を流れる電流により生じる磁場の影響および導線の抵抗は無視できるものとする.回路に力を加えることにより,回路は形を変えずに一定の速さ$\dfrac{L}{2T}[\rm m/s]$で左向きに動いている.時刻$t=0\rm s$では$\rm ae$は磁場領域の右端$\rm QR$に重なっており,時刻$t=T[\rm s]$では,$\rm ae$は磁場領域の左端$\rm PS$に重なっていた.ただし,回路は常に紙面内にあるものとする.次の問いには,$L$,$B$,$T$,$t$を用いて答えよ.
(1) $0<t<T$を満たす$t$において,線分$\rm ab$に流れる電流$[\rm A]$の大きさを求めよ.また,回路を一定の速さ$\dfrac{L}{2T}[\rm m/s]$で動かすために回路に加えなければならない力の大きさ$[\rm N]$を求めよ.
(2) $T<t<2T$を満たす$t$において,回路を一定の速さ$\dfrac{L}{2T}[\rm m/s]$で動かすために回路に加えなければならない力の大きさ$[\rm N]$を求めよ.
(3) $2T<t<3T$を満たす$t$において回路を一定の速さ$\dfrac{L}{2T}[\rm m/s]$で動かすために回路に加えなければならない力の大きさ$[\rm N]$を求めよ.
<解答>
(1)

$\rm ae$部分が磁場中を運動しているので,誘導起電力が生じます.
速さが$\dfrac{L}{2T}$で,磁束密度の大きさ$B$,長さが$L$なので,誘導起電力の大きさは,
$\dfrac{L}{2T}\cdot B\cdot L=\dfrac{BL^{2}}{2T}$
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は,PQの長さを$l$,PQ方向に垂直な速さを$v_{\perp}$,導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば,
$V=v_{\perp}Bl$

今回の問題では,ダイオードがあるので,ダイオードに電流が流れるのか流れないのかを調べる必要があります.
$\rm ae$部分の導線には,順方向$(\rm a\rightarrow e)$に起電力が生じているので,ダイオード$\rm D_{1}$には電流が流れます.(他には電池がないので,明らかでしょう.)
そして,ダイオード$\rm D_{2}$には,とりあえず電流が流れないものとして考えてみましょう.
順方向は抵抗ゼロで電流が流れ,逆方向には抵抗無限大になるダイオードを考える.
このとき,ダイオードに電流が流れるか流れかは,次のように判断する.
- ダイオードには電流が流れないと仮定して回路の式を立てる.
- 1.の結果AよりBの電位が高ければ,そのままダイオードに電流は流れないし,BよりAの電位が大きければ,ダイオードに電流が流れるものとして,もう一度回路の式を立てる.
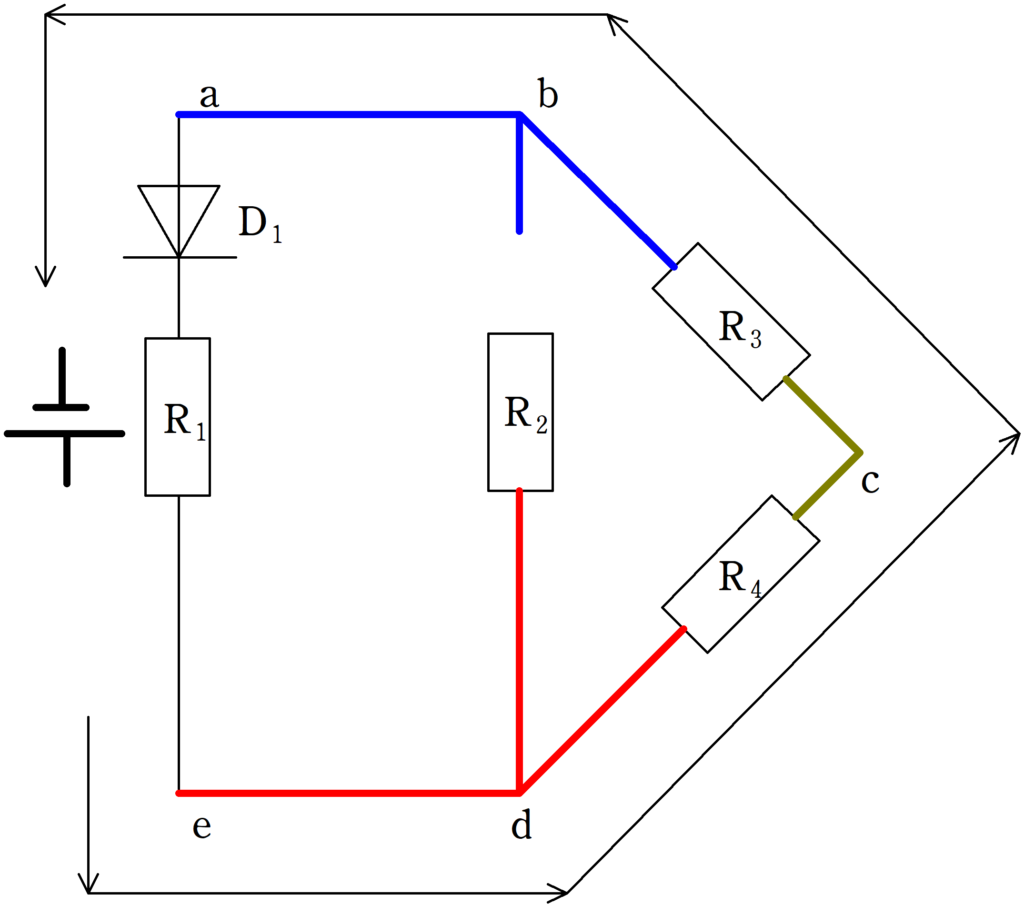

ダイオード$\rm D_{2}$に電流が流れないものとすると,上図のような向きに電流が流れます.すると,抵抗に電流が流れる方向に電位が下がるので,結果,$\rm d$よりも$\rm b$の方が電位が低くなるため,ダイオード$\rm D_{2}$には電流が流れません.
回路の流れる電流を$i_{1}$として,キルヒホッフ則を立てましょう.
★ キルヒホッフ則
$\dfrac{BL^{2}}{2T}-Ri_{1}-Ri_{1}-Ri_{1}=0$
$\therefore i_{1}=\dfrac{BL^{2}}{6RT}[\rm A]$ (答)

回路に加える力は,電磁力のはたらく向きと逆方向で大きさは同じです.
なので,電磁力の大きさを求めればよいことがわかります.
電流の大きさを$I$,磁束密度の大きさを$B$とする.磁場の方向と電流の方向が垂直な関係にあるとき,導線の長さ$l$あたりにはたらく電磁力の大きさ$F$は
$F=IBl$
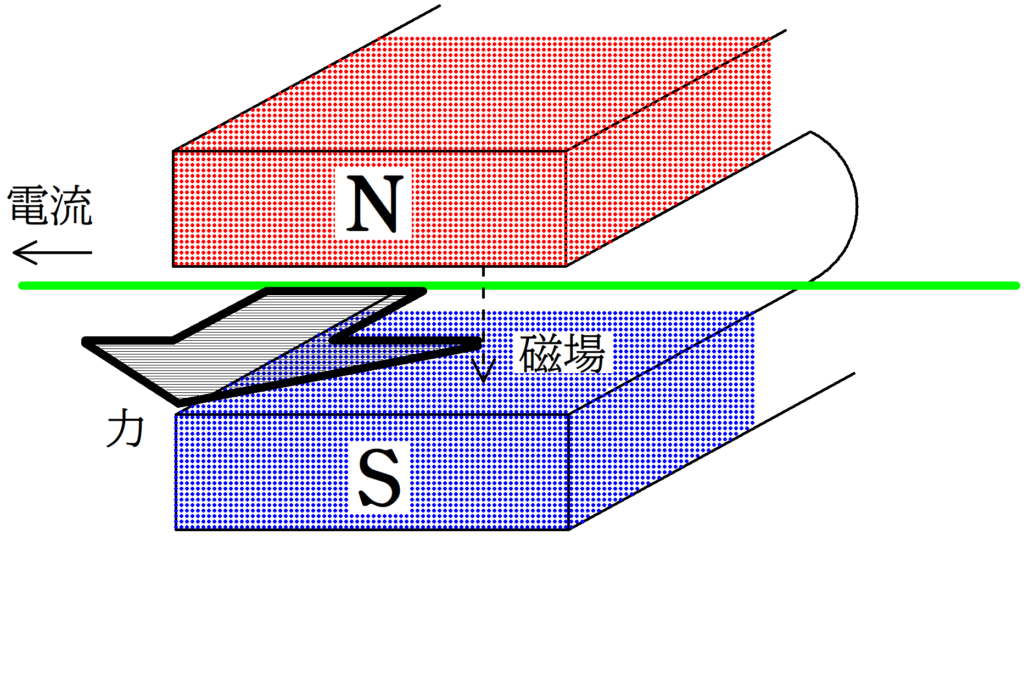
電磁力の向きはフレミング左手の法則にしたがいます.
※ 左手の親指→力の向き,人差し指→磁場の向き,中指→電流の向き
★ $\rm ae$にはたらく電磁力$F_{1}$
$\eqalign{F_{1}&=i_{1}BL\\&=\dfrac{BL^{2}}{6RT}\cdot BL\\&=\dfrac{B^{2}L^{3}}{6RT}}$
したがって,回路に加える外力の大きさは,$\dfrac{B^{2}L^{3}}{6RT}[\rm N]$(答)

別解として,
外力の仕事率=回路の消費電力
の式を立てて求めることもできます.
★ 外力の仕事率=抵抗で消費する電力の和
$\eqalign{F_{1}\cdot \dfrac{L}{2T}&=i_{1}^{2}R\times 3\cr F_{1}\cdot \dfrac{L}{2T}&=\left(\dfrac{BL^{2}}{6RT}\right)^{2}\times 3R\cr F_{1}&=\dfrac{B^{2}L^{3}}{6RT}}$ (別解答)
(2)
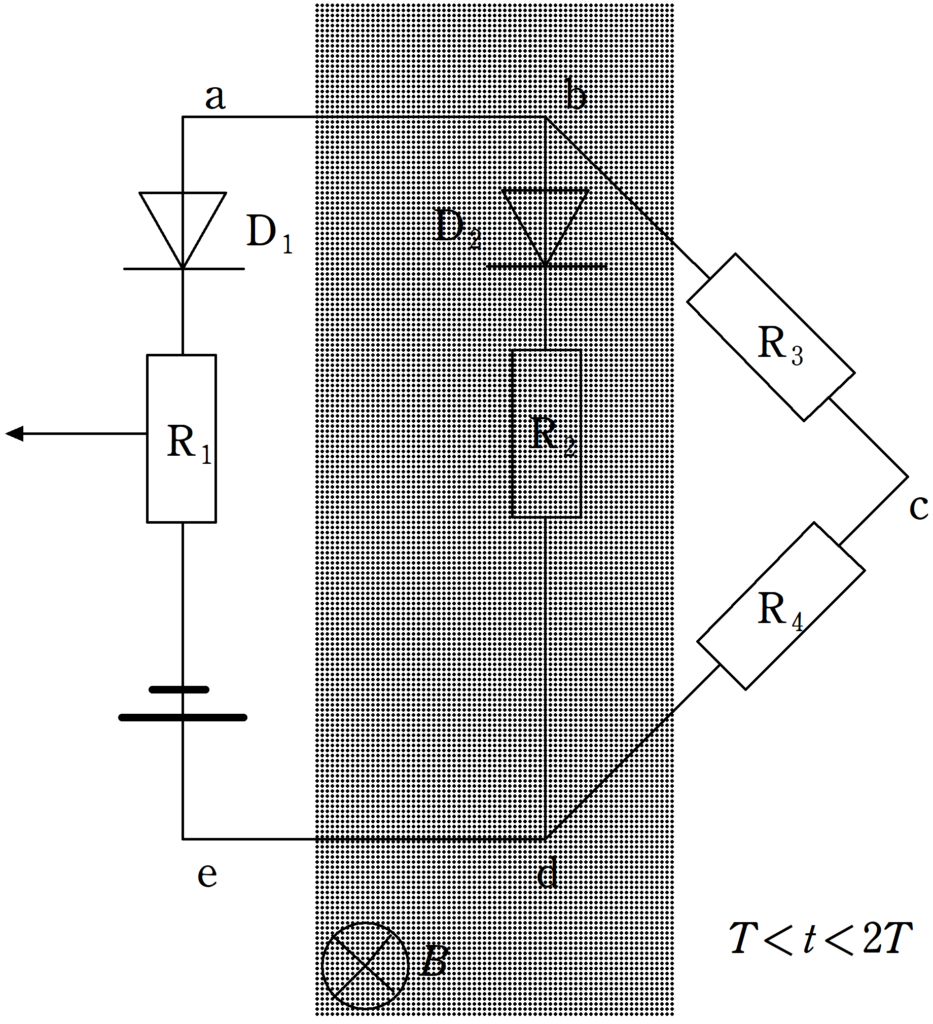

$T<t<2T$のとき,$\rm bd$部分と$\rm bc$部分と$\rm cd$部分に誘導起電力が生じます.
$\rm bd$部分に生じる起電力$V_{\rm bd}$は(1)と同様に
$V_{\rm bd}=\dfrac{BL^{2}}{2T}$
です.
$\rm bc$部分と$\rm cd$部分については丁寧に考えていきましょう.
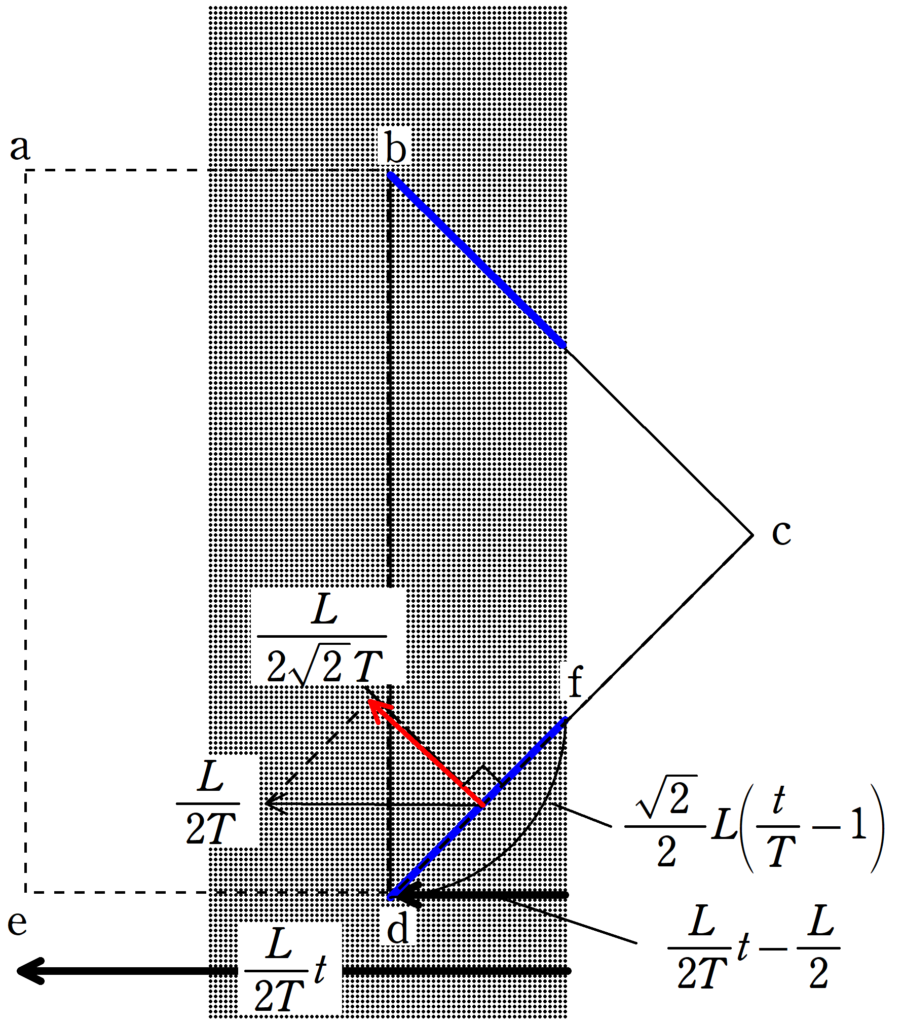

時刻$t$において,$\rm ae$部分は$\dfrac{L}{2T}t$だけ移動しています.$\rm ed$間の距離が$\dfrac{L}{2}$なので,$\rm bd$部分は$\dfrac{L}{2T}t-\dfrac{L}{2}$だけ磁場がかかっている領域に進入しています.
$\rm cd$部分の磁場に進入している部分$\rm fd$は,
$\left(\dfrac{L}{2T}t-\dfrac{L}{2}\right)\cdot \sqrt{2}$ $\dots (\ast)$
となります.
また,導体棒$\rm fd$の長さ方向に垂直な速度成分は
$\eqalign{\dfrac{L}{2T}\cos\dfrac{\pi}{4}&=\dfrac{L}{2\sqrt{2}T}}$ $\dots (2\ast)$
$(\ast)$,$(2\ast)$より,$\rm fd$部分に生じる起電力$V_{\rm fd}$は
$\eqalign{V_{\rm fd}&=\dfrac{L}{2\sqrt{2}T}\cdot B\cdot \left(\dfrac{L}{2T}t-\dfrac{L}{2}\right)\cdot \sqrt{2}\\&=\dfrac{BL^{2}}{4T}\left(\dfrac{t}{T}-1\right)}$
$\rm bc$部分も同様に考えると,$\dfrac{BL^{2}}{4T}\left(\dfrac{t}{T}-1\right)$の起電力が生じ,$\rm bcd$部分は合わせて
$\eqalign{\dfrac{BL^{2}}{4T}\left(\dfrac{t}{T}-1\right)\cdot 2\\=\dfrac{BL^{2}}{2T}\left(\dfrac{t}{T}-1\right)}$
ここで,$T<t<2T$のとき,
$0<\dfrac{t}{T}-1<1$
なので,$\rm bd$部分の起電力と$\rm bcd$部分の起電力では$\rm bd$部分の起電力の方が常に大きいことが確認できます.
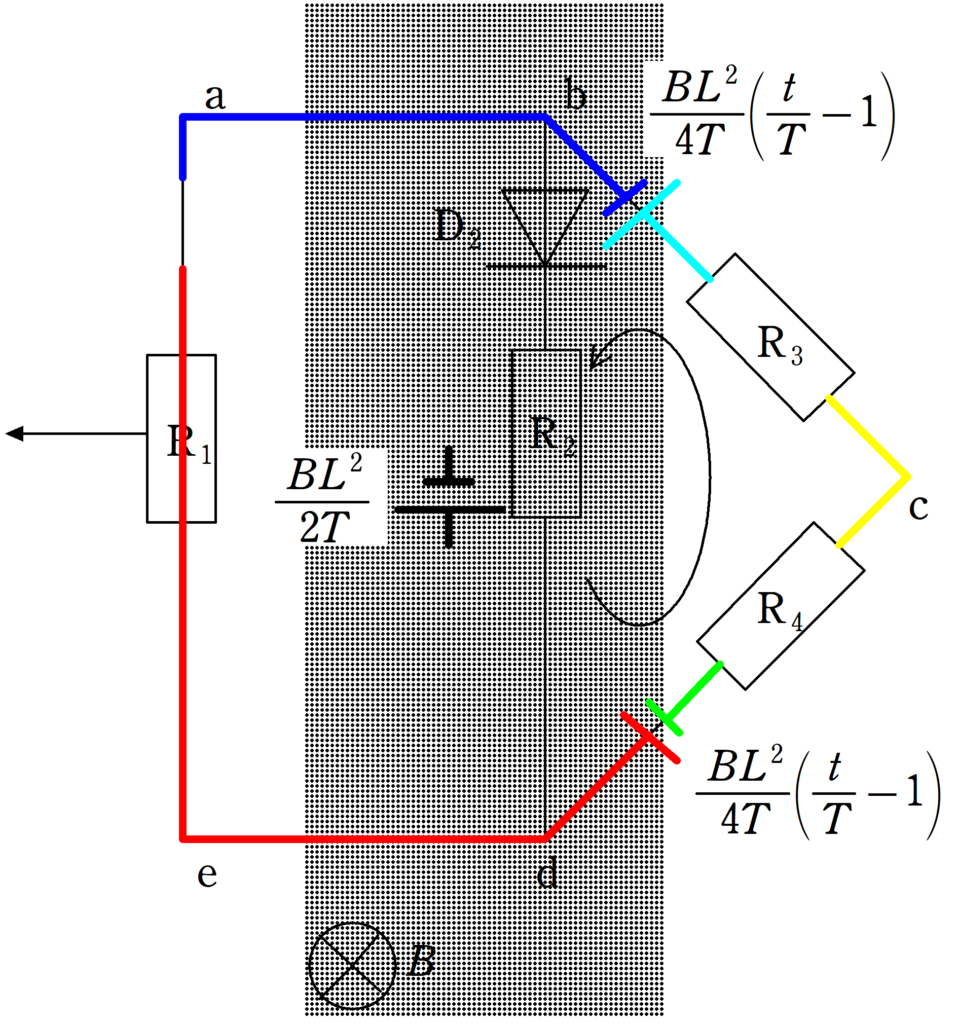

じゃあ,上図の矢印の向きに電流が流れるんだね.
流れる電流を$i_{2}$として,キルヒホッフ則を立てましょう.
★ キルヒホッフ則
$\eqalign{\dfrac{BL^{2}}{2T}-\dfrac{BL^{2}}{4T}\left(\dfrac{t}{T}-1\right)\cdot 2-Ri_{2}\cdot 3&=0\cr 3Ri_{2}&=\dfrac{BL^{2}}{2T}\left(2-\dfrac{t}{T}\right)\cr i_{2}&=\dfrac{BL^{2}}{6RT}\left(2-\dfrac{t}{T}\right)}$

外力は,(1)の別解で紹介した
外力の仕事率=抵抗で消費する電力の和
で計算してみましょう.
外力を$F_{2}$とします.
★ 外力の仕事率=抵抗で消費する電力の和
$\eqalign{F_{2}\cdot \dfrac{L}{2T}&=i_{2}^{2}R\times 3\cr F_{2}\cdot \dfrac{L}{2T}&=\left\{\dfrac{BL^{2}}{6RT}\left(2-\dfrac{t}{T}\right)\right\}^{2}\cdot R\times 3\cr F_{2}&=\dfrac{B^{2}L^{3}}{6RT}\left(2-\dfrac{t}{T}\right)^{2}}$
したがって,回路に加える外力の大きさは$\dfrac{B^{2}L^{3}}{6RT}\left(2-\dfrac{t}{T}\right)^{2}[\rm N]$(答)
(3)
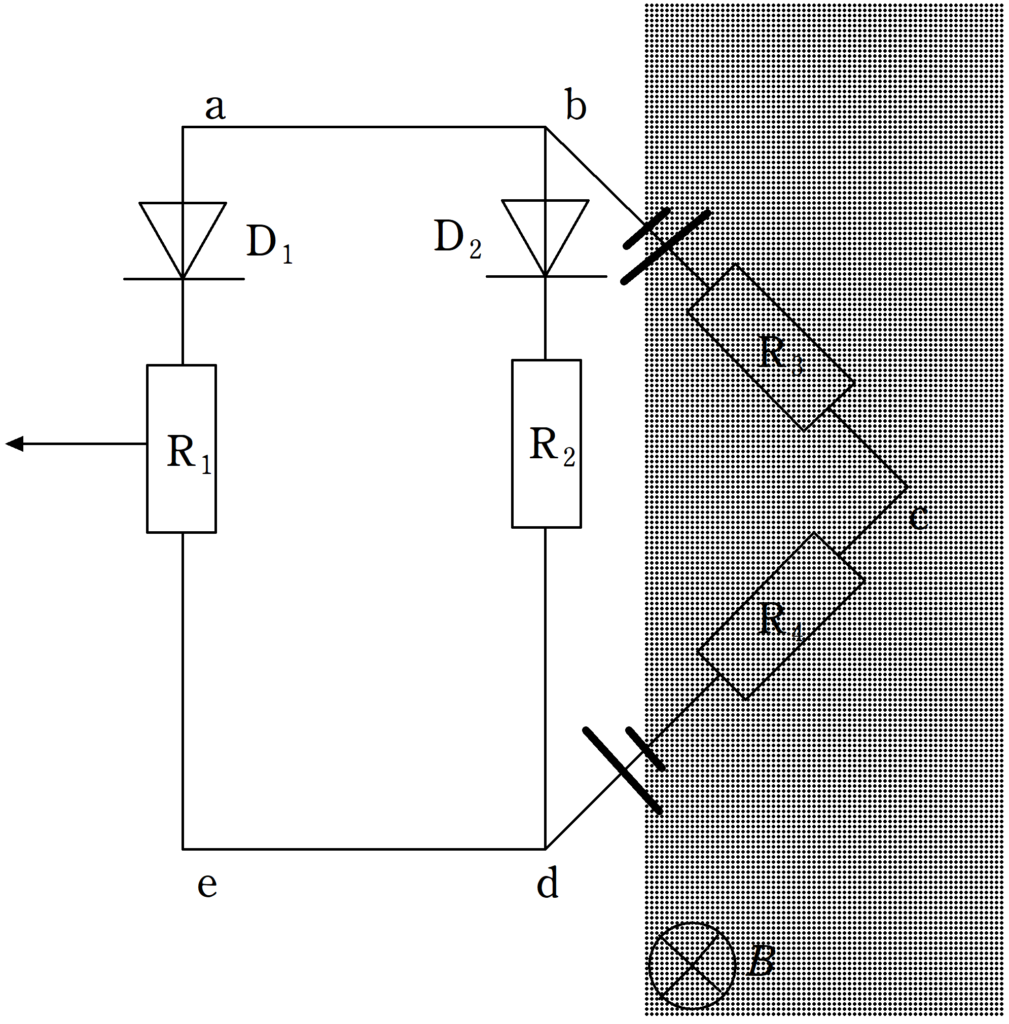

最後に,$2T<t<3T$のときは,上図のような誘導起電力が生じ,ダイオード$\rm D_{1}$,$\rm D_{2}$には逆方向に電流を流そうとするため,電流は流れません.
したがって,回路に力を加えなくとも,等速度運動します.
回路に加える力は$0[\rm N]$(答)


コメント
[…] […]
[…] […]