[1]
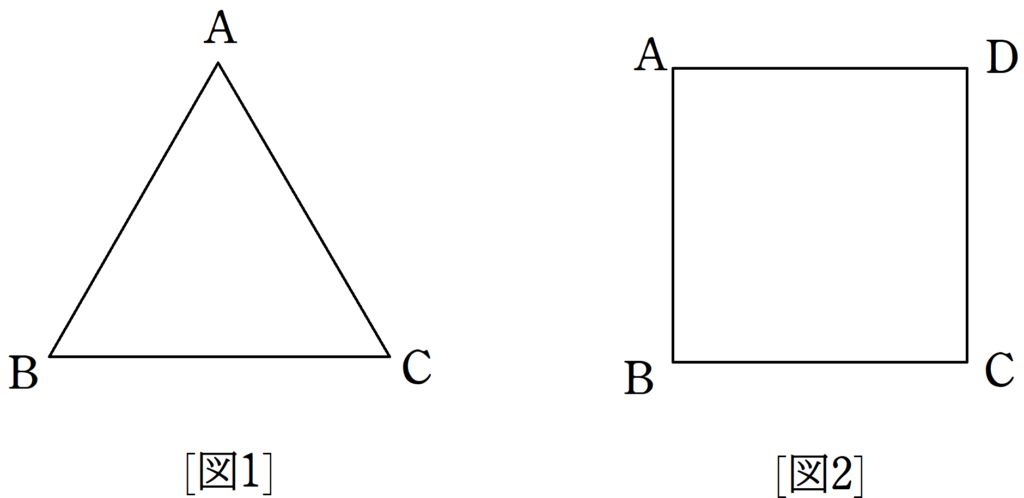
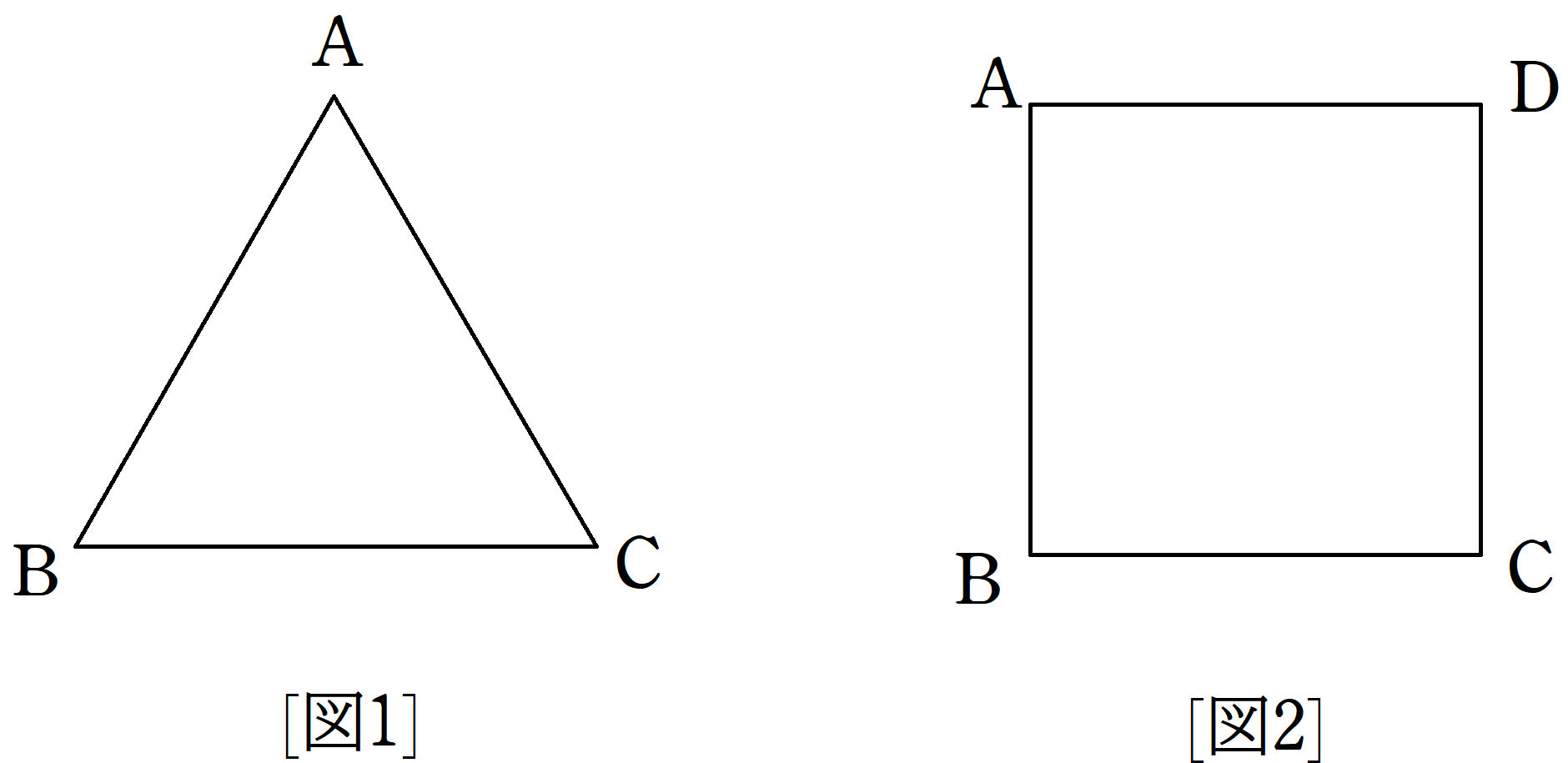
図1のように,正三角形$\rm ABC$の辺に沿って,質量$m$の質点が速さ$v$で$\rm A\rightarrow \rm B\rightarrow \rm C$の向きにまわっている.このとき,次の問いに答えよ.
(1) 点$\rm A$で質点が受ける力積の向きを図にかけ.
(2) 点$\rm A$で受ける力積の大きさを求めよ.
[2]
図2のように,正方形${\rm ABCD}$の辺に沿って,質量$m$の質点が速さ$v$で${\rm A}\rightarrow {\rm B}\rightarrow {\rm C}\rightarrow {\rm D}$の向きにまわっている.このとき,次の問いに答えよ.
(1) 点$\rm A$で質点が受ける力積の向きを図にかけ.
(2) 点$\rm A$で受ける力積の大きさを求めよ.
<解答>
時間$\varDelta t$の間の速度の変化を$\varDelta \vec{v}$とする.質量を$m$とすると
$m\varDelta \vec{v}=$力積
の関係がある.
[1]

(1)の図示は次のようになります.(答)
今回は,2次元の問題なので,ベクトルの成分表示を使って計算してみましょう.
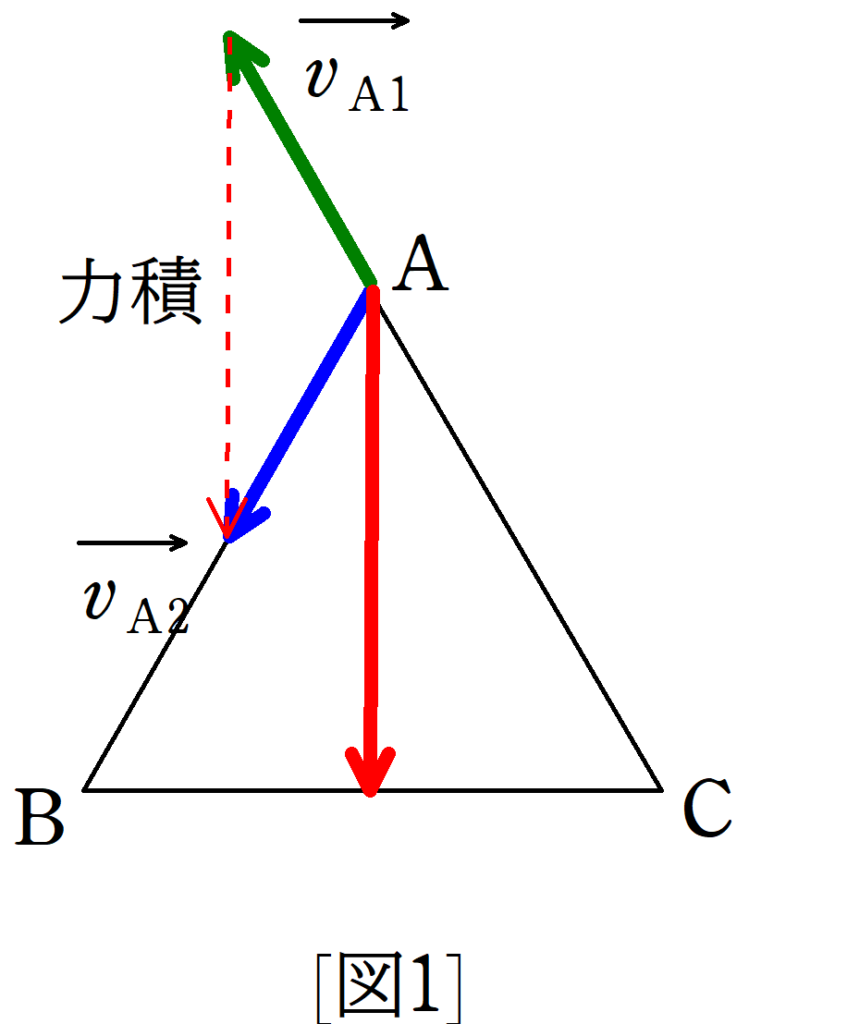

${\rm C\rightarrow A\rightarrow B}$と移動するなかで,$\rm A$で方向転換する前の速度ベクトルを$\overrightarrow{v_{\rm A1}}$,転換後の速度ベクトルを$\overrightarrow{v_{\rm A2}}$とすると,運動量変化$\varDelta I$は
$\varDelta I=m\overrightarrow{v_{\rm A2}}-m\overrightarrow{v_{\rm A1}}$
となります.
これを成分表示してみると,次のようになります.$x$,$y$方向の正の方向は下図の向きとします.
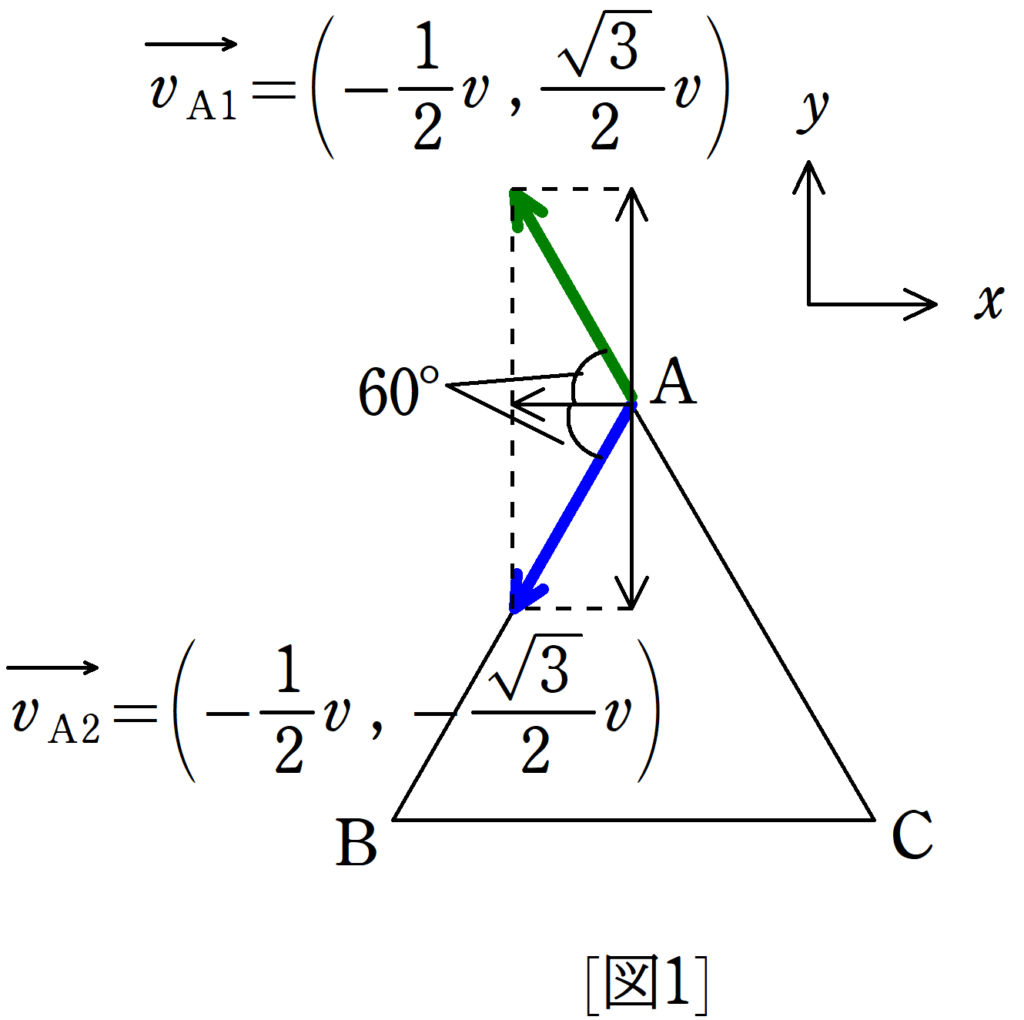
$\overrightarrow{v_{\rm A1}}=\left(-\dfrac{1}{2}v , \dfrac{\sqrt{3}}{2}v\right)$,$\overrightarrow{v_{\rm A2}}=\left(-\dfrac{1}{2}v , -\dfrac{\sqrt{3}}{2}v\right)$より
$\eqalign{\varDelta I&=m\overrightarrow{v_{\rm A2}}-m\overrightarrow{v_{\rm A1}}\\&=m\left(-\dfrac{1}{2}v , -\dfrac{\sqrt{3}}{2}v\right)-m\left(-\dfrac{1}{2}v , \dfrac{\sqrt{3}}{2}v\right)\\&=(0 , -\sqrt{3}mv)}$

運動量変化が$y$軸の負の向きに$\sqrt{3}mv$なので,質点が受ける力積の大きさも$\sqrt{3}mv$(答)
[2]
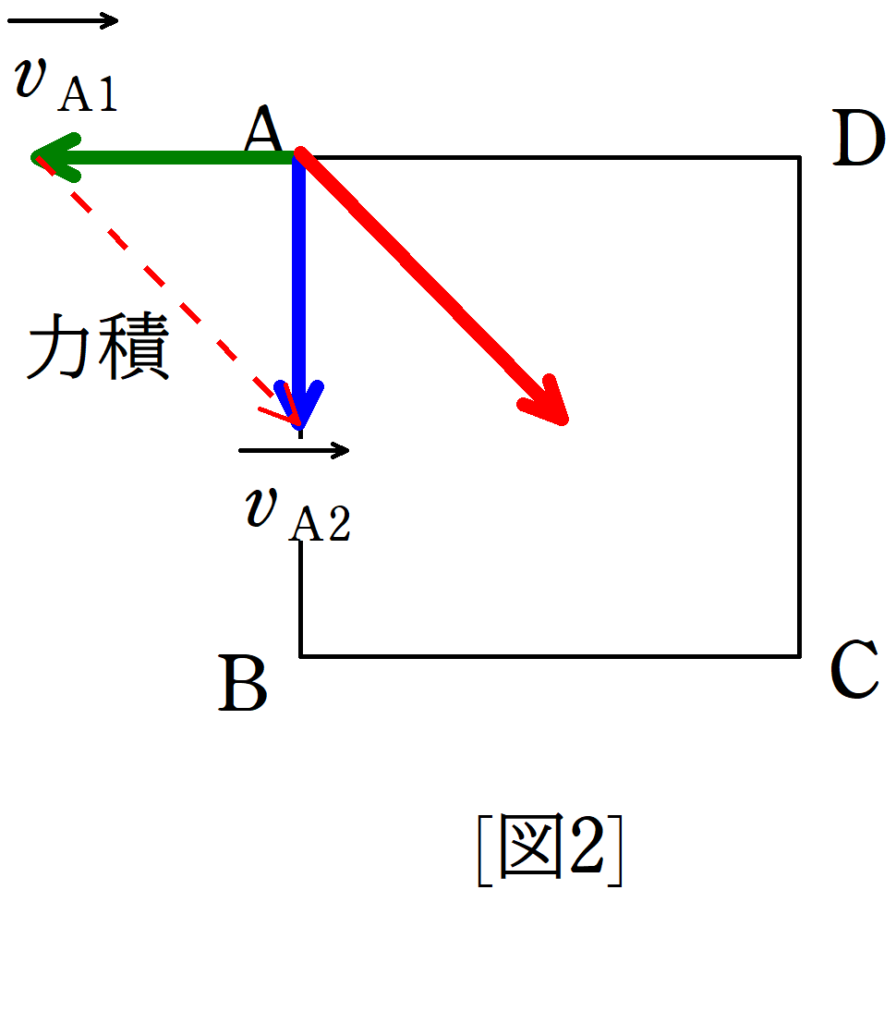

(1)の図示は上のようになります.(答)
この問題も,ベクトルの成分表示を使って計算してみましょう.
${\rm C\rightarrow A\rightarrow B}$と移動するなかで,$\rm A$で方向転換する前の速度ベクトルを$\overrightarrow{v_{\rm A1}}$,転換後の速度ベクトルを$\overrightarrow{v_{\rm A2}}$とすると,運動量変化$\varDelta I$は
$\varDelta I=m\overrightarrow{v_{\rm A2}}-m\overrightarrow{v_{\rm A1}}$
となります.
これを成分表示してみると,次のようになります.$x$,$y$方向の正の方向は下図の向きとします.
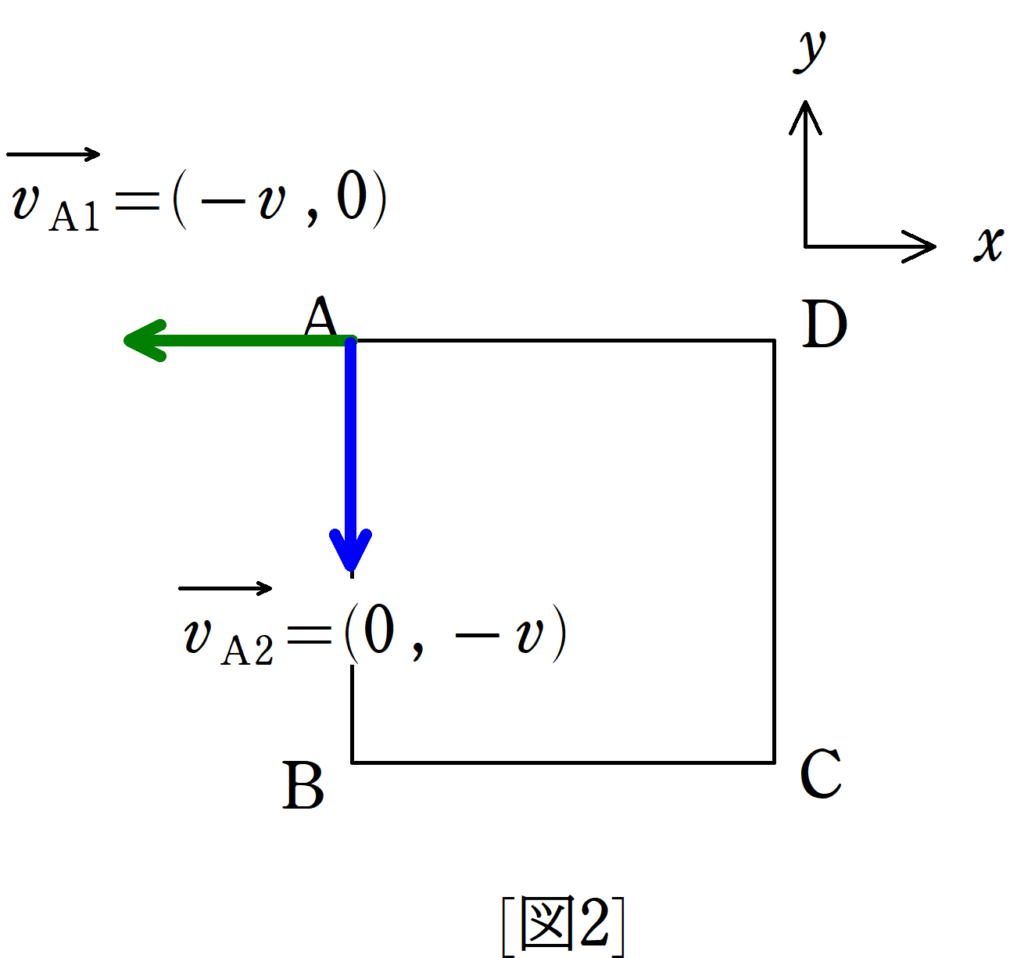
$\overrightarrow{v_{\rm A1}}=(-v , 0)$,$\overrightarrow{v_{\rm A2}}=(0 , -v)$より
$\eqalign{\varDelta I&=m\overrightarrow{v_{\rm A2}}-m\overrightarrow{v_{\rm A1}}\\&=m(0 , -v)-m(-v , 0)\\&=(mv , -mv)}$

運動量変化が$(mv , -mv)$なので,力積も$(mv , -mv)$です.
その大きさは,$\sqrt{2}mv$(答)


コメント
[…] [演習問題]運動量変化と力積2運動量変化と力積ダウンロード問題図1のよう… 問題 […]
[…] [演習問題]運動量変化と力積2運動量変化と力積ダウンロード問題図1のよう… […]