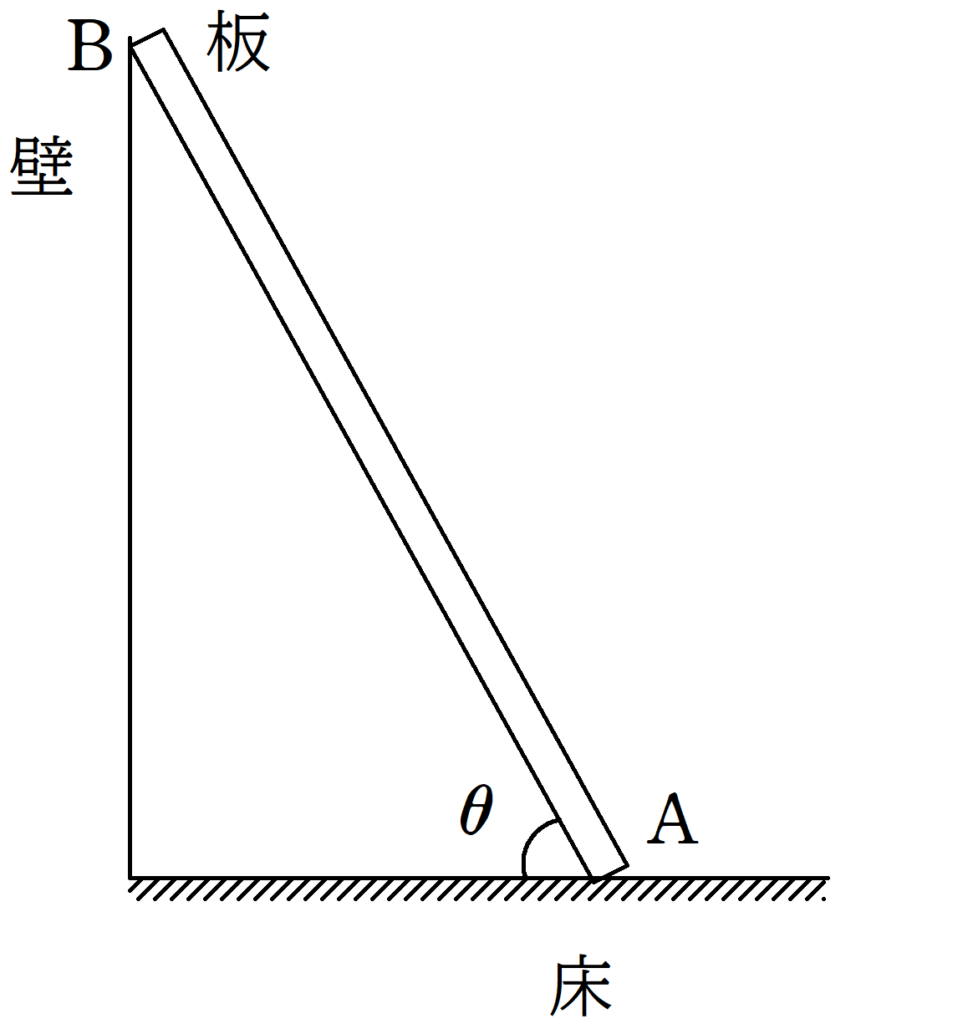
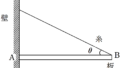
水平であらい床と，鉛直でなめらかな壁に長さ$l$で質量が$m$であり，一様な密度の板が立てかけられている．板と床とのなす角が$\theta(0<\theta<\dfrac{\pi}{2})$のとき，板は静止していた．重力加速度の大きさを$g$として次の問いに答えよ．
(1) 図の点$\rm A$において，板にはたらく垂直抗力の大きさを$N$，摩擦力の大きさを$f$，点$\rm B$にはたらく垂直抗力の大きさを$R$とする．板に関する水平方向と鉛直方向それぞれのつり合いの式を立てよ．
(2) 点$\rm A$まわりの力のモーメントのつり合いの式を立て，$R$を$m$，$g$を用いて表せ．
(3) 床と板との間の静止摩擦係数を$\mu$とする．板が静止する条件を$\mu$と$\theta$を用いて表せ．
<解答>
(1)
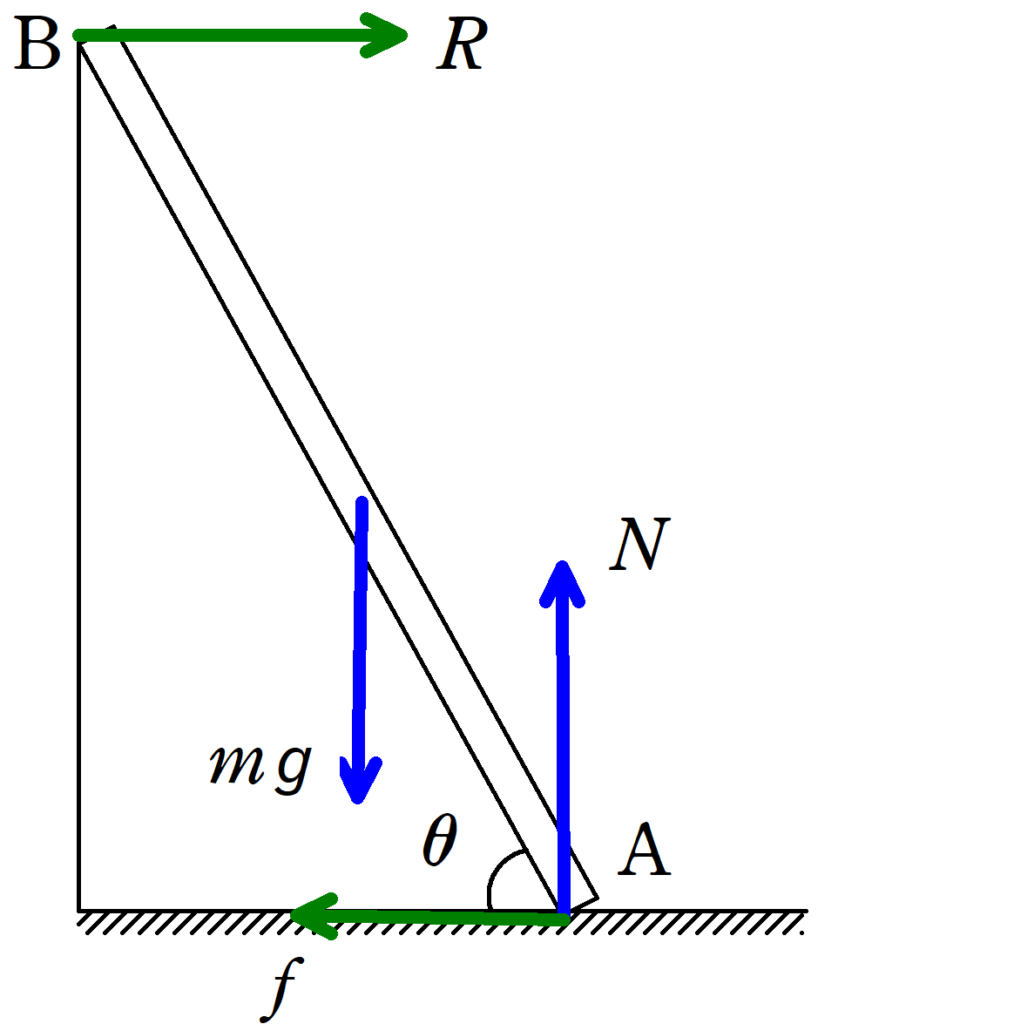
板にはたらく力を図示すると上のようになります．
★ 水平方向のつり合いの式
$R=f$ $\dots (\ast)$ (答)
★ 鉛直方向のつり合いの式
$N=mg$ $\dots (2\ast)$ (答)
(2)
次に力のモーメントのつり合いの式を立てます．
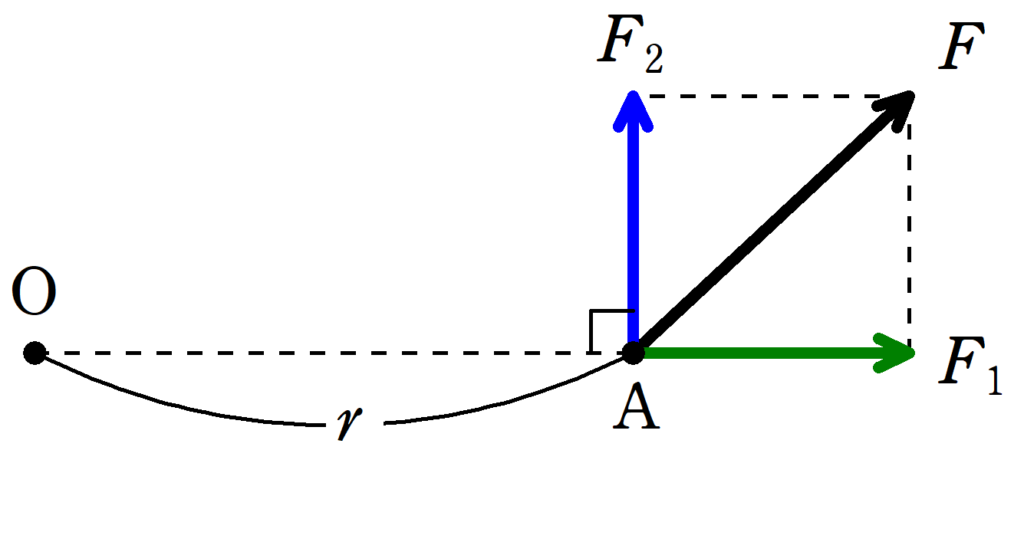
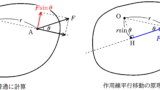
中心$\rm O$から距離$r$の点$\rm A$を始点とした大きさ$F$の力がはたらいている．この力の$\rm OA$方向の成分を$F_{1}$，$\rm OA$に垂直な成分を$F_{2}$とすると，力$F$の点$\rm O$まわりの力のモーメントの大きさ$N$は
$N=rF_{2}$
中心を$\rm O$とし，ある始点にはたらく力のモーメントを計算するとき，力の作用線上のどこに移動させても力のモーメントは同じである．
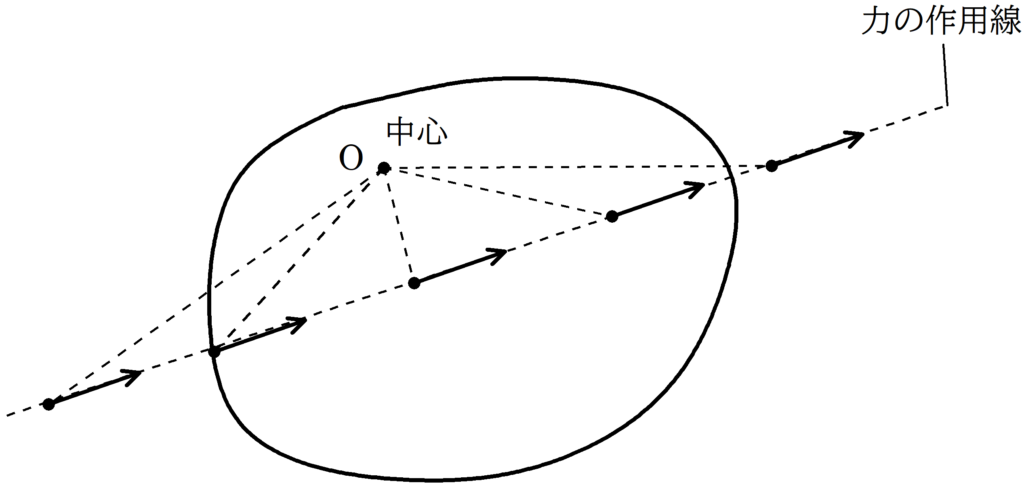
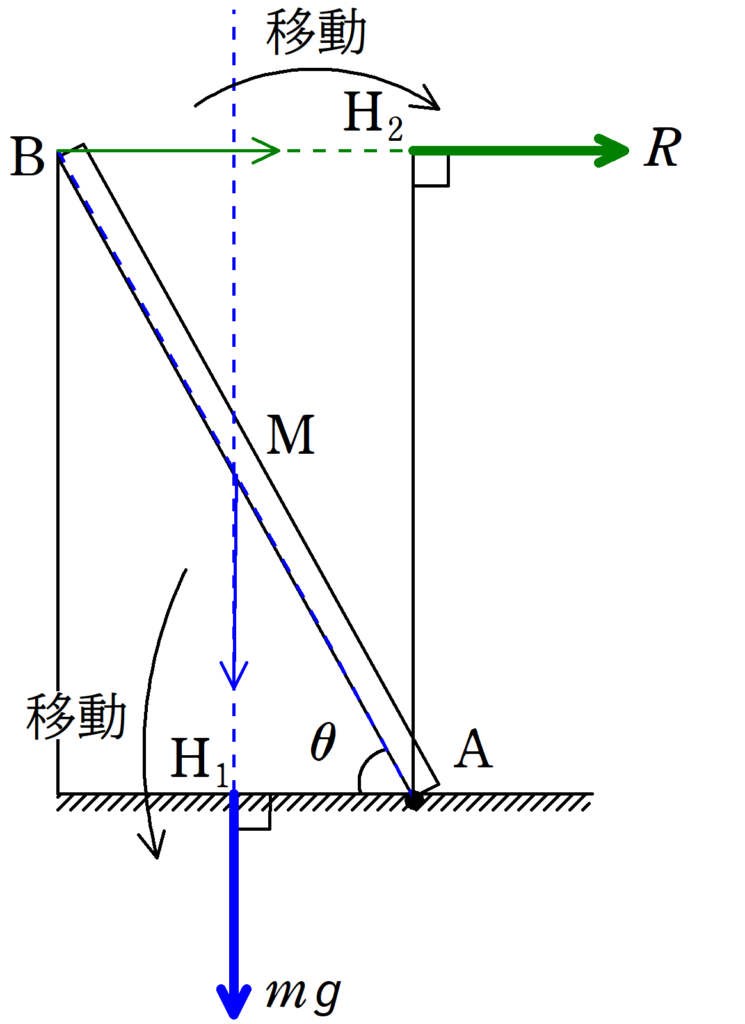
点$\rm A$から板の重力の作用線に向かって垂線を引き，その交点を$\rm H_{1}$とし，同じく点$\rm A$から垂直抗力$R$の作用線に向かって垂線を引き，その交点を$\rm H_{2}$とします．
それぞれの力の始点を$\rm H_{1}$，$\rm H_{2}$まで移動することで，中心を$\rm A$としたときの力は垂直成分のみとなります．
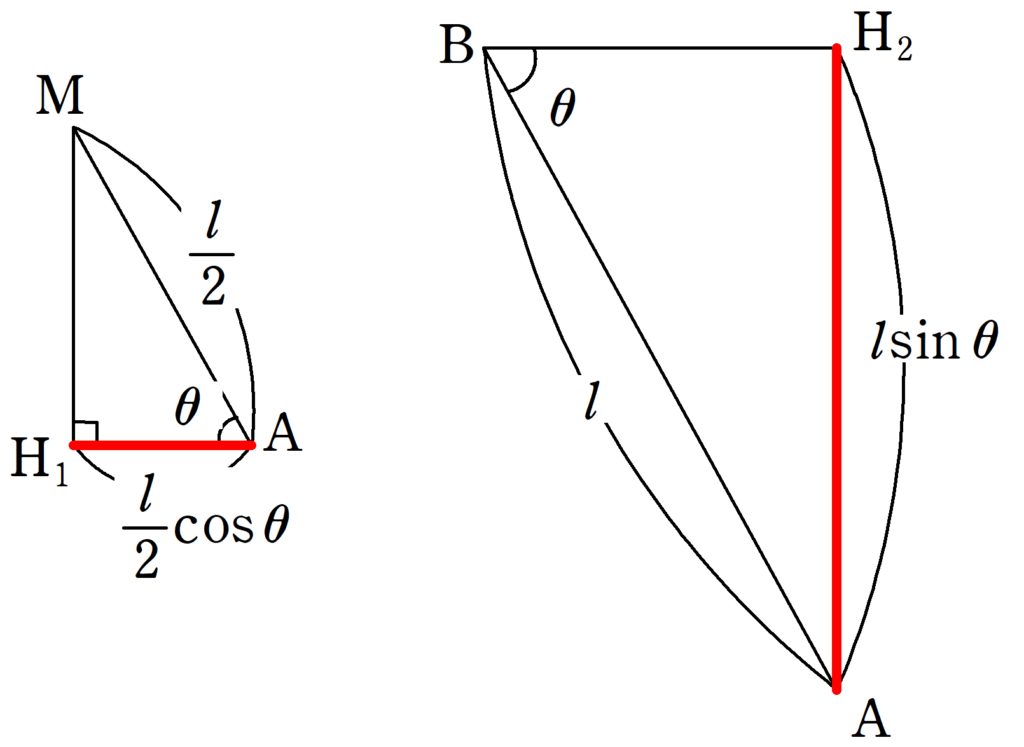
上図より，
${\rm AH_{1}}=\dfrac{l}{2}\cos\theta$
${\rm AH_{2}}=l\sin\theta$
から，力のモーメントのつり合いの式を立てましょう．
★ 力のモーメントのつり合いの式
$\eqalign{{\rm AH_{1}}\cdot mg&={\rm AH_{2}}\cdot R\cr \dfrac{l}{2}\cos\theta \cdot mg&=l\sin\theta \cdot R\cr R&=\dfrac{\cos\theta}{2\sin\theta}mg=\dfrac{mg}{2\tan\theta}}$
したがって，$R=\dfrac{mg}{2\tan\theta}$(答)
(3)
$(\ast)$と(2)より
$f=R=\dfrac{mg}{2\tan\theta}$
だね．また，$(2\ast)$より，床と板の間の垂直抗力の大きさが$N=mg$となります．板がすべらないためには，静止摩擦力が最大静止摩擦力より小さければよいね．つまり
$f<\mu N$
より
$\dfrac{mg}{2\tan\theta}<\mu mg$
$\therefore \dfrac{1}{2\tan\theta}<\mu$ (答)
物体がすべらない条件は，静止摩擦力が最大静止摩擦力より小さいときである．
静止摩擦力の大きさを$f$，静止摩擦係数を$\mu$，摩擦力がはたらく面の垂直抗力の大きさを$N$とすれば
$f<\mu N$
の条件を満たせば面に対してすべらない．
コメント
[…] 力のモーメント演習2力のモーメント演習ダウンロード問題水平であらい床… […]