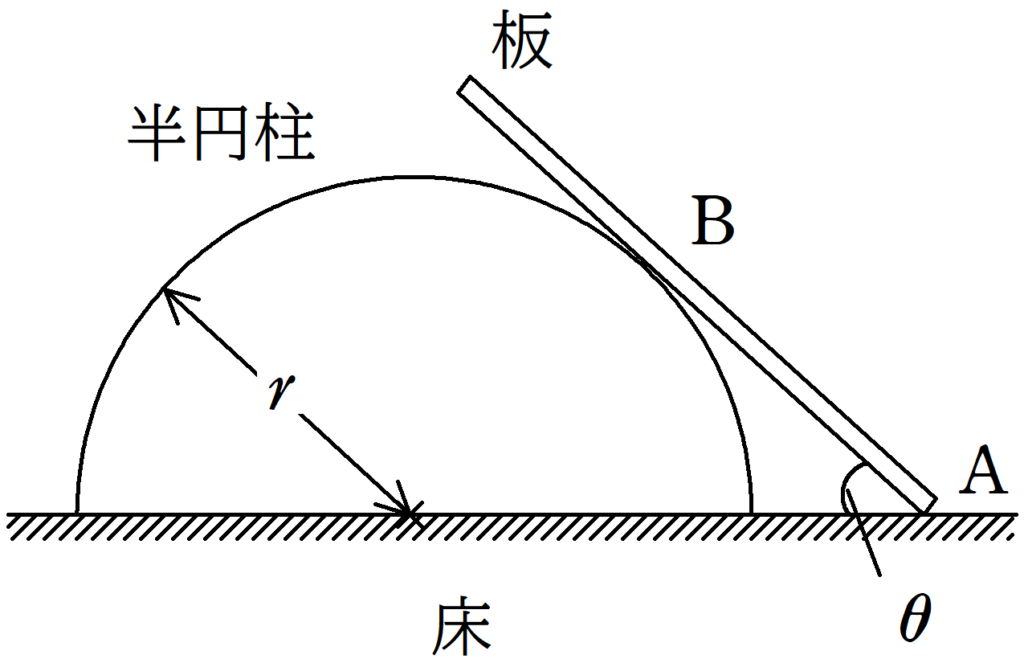
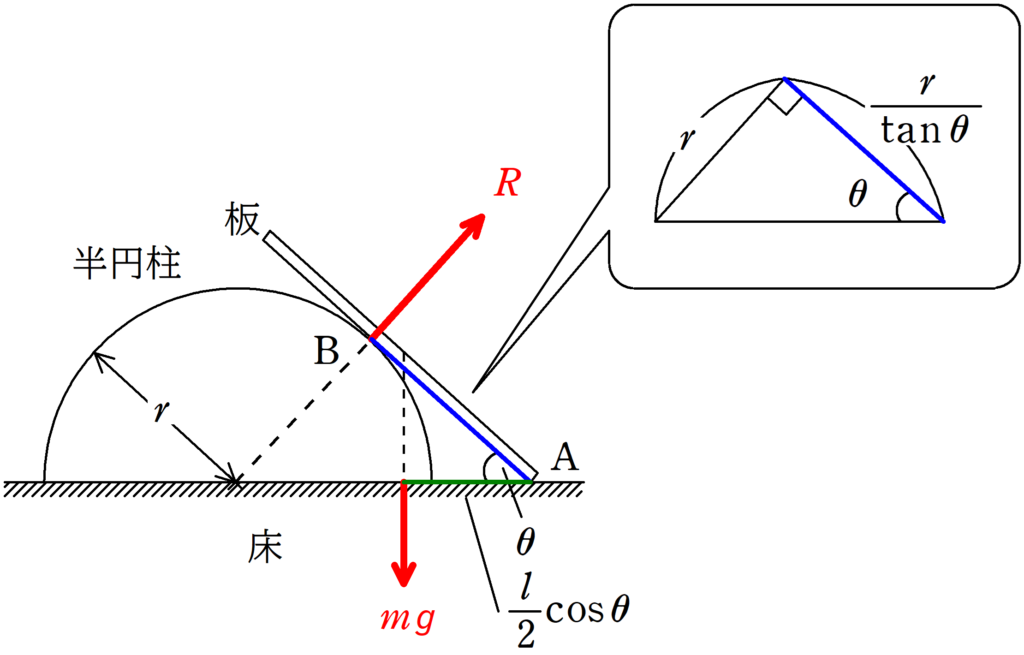
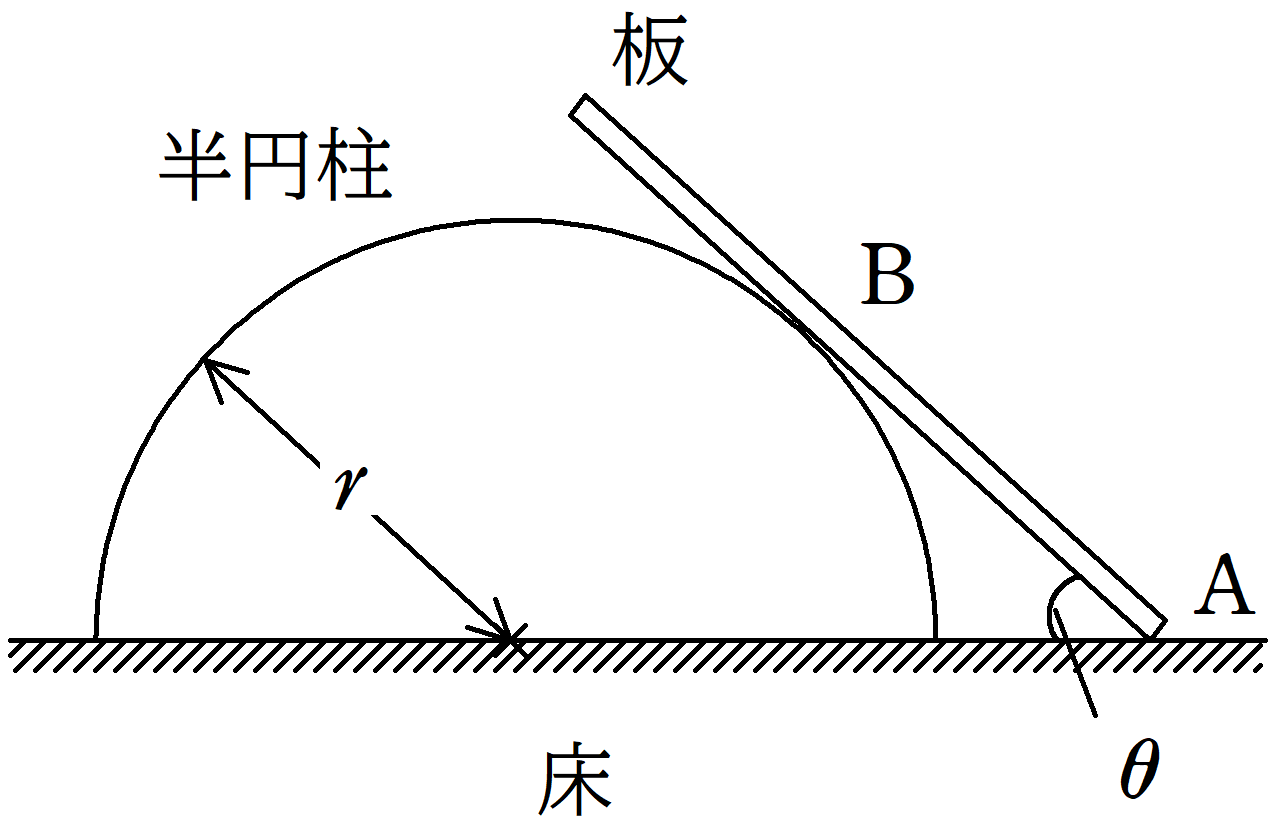
図のように,水平な床の上に固定された底面の半径が$r$の半円柱に質量$m$,長さ$l$の密度が一様でまっすぐな板をたてかけた.板と半円柱の間の摩擦は無視をする.板と床とのなす角は$0<\theta<\dfrac{\pi}{2}$であり,重力加速度の大きさを$g$として,次の問いに答えよ.
(1) 図の$\rm B$にはたらく板と半円柱の間の垂直抗力の大きさを$R$,$\rm A$点にはたらく水平な床と板の間の垂直抗力の大きさを$N$,摩擦力の大きさを$f$とするとき,板に関する水平方向のつり合いの式と鉛直方向のつり合いの式をそれぞれ立てよ.
(2) 点$\rm A$まわりの板に関する力のモーメントのつり合いの式を立てよ.
(3) (1),(2)より,$f$,$N$,$R$を$m$,$g$,$r$,$l$,$\theta$を用いて表せ.
<解答>
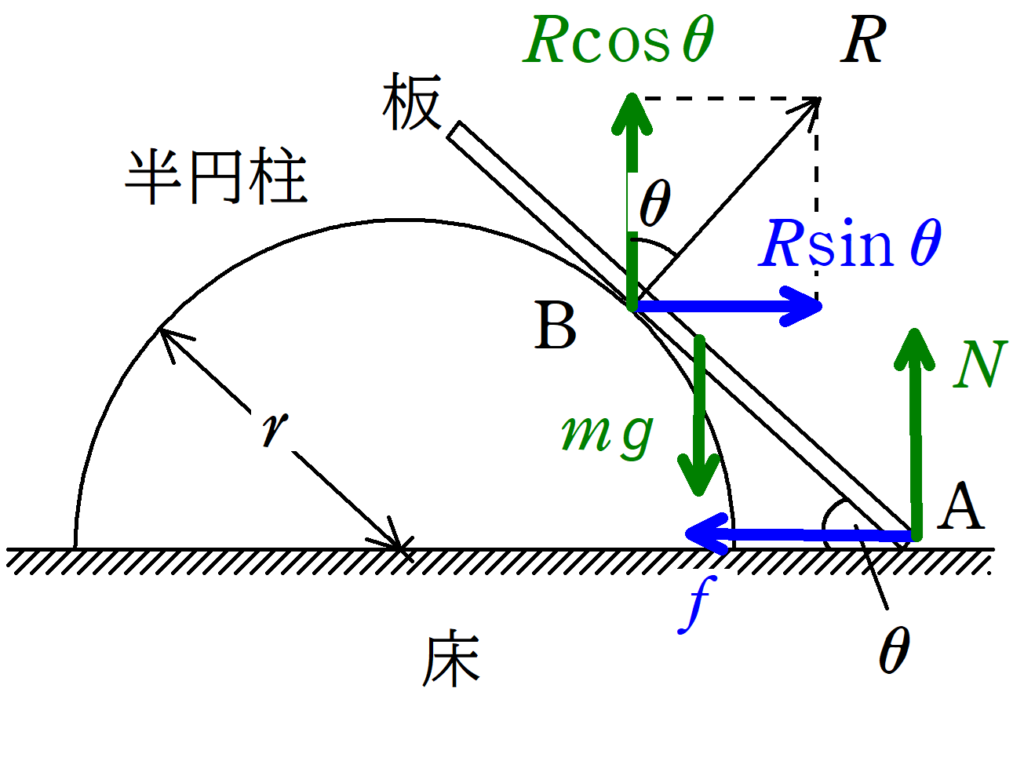

板にはたらく力を作図すると,上図のようになります.
点$\rm B$にはたらく垂直抗力を水平成分と鉛直成分に分けるとそれぞれ$R\sin\theta$,$R\cos\theta$となります.
それでは,水平方向と鉛直方向のつり合いの式を立てましょう.
★ 水平方向のつり合いの式
$f=R\sin\theta$ $\dots (\ast)$ (答)
★ 鉛直方向のつり合いの式
$N+R\cos\theta=mg$ $\dots (2\ast)$ (答)
(2)
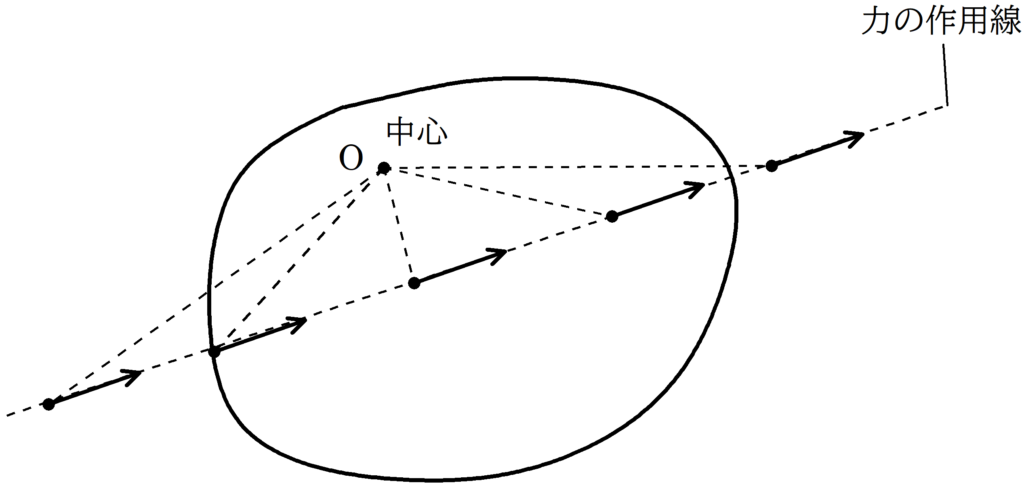
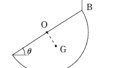
中心を$\rm O$とし,ある始点にはたらく力のモーメントを計算するとき,力の作用線上のどこに移動させても力のモーメントは同じである.
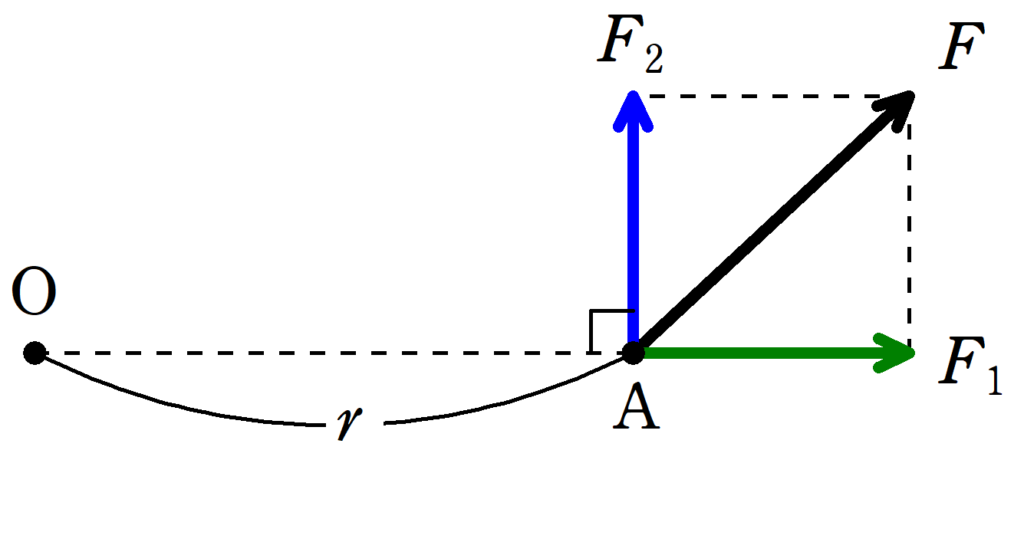
中心$\rm O$から距離$r$の点$\rm A$を始点とした大きさ$F$の力がはたらいている.この力の$\rm OA$方向の成分を$F_{1}$,$\rm OA$に垂直な成分を$F_{2}$とすると,力$F$の点$\rm O$まわりの力のモーメントの大きさ$N$は
$N=rF_{2}$

点$\rm A$まわりのモーメントなので,点$\rm A$にはたらく力のモーメントは0です.
点$\rm B$にはたらく垂直抗力の力のモーメントは力の分解をする前のモーメントを考えた方が楽でしょう.
下図のように$\rm A$と$\rm B$の距離は$\dfrac{r}{\tan\theta}$です.
また,重力に関しては,作用線平行移動の原理を用いて計算しましょう.
点$\rm A$と重力の作用線の距離は$\dfrac{l}{2}\cos\theta$です.
★ 点$\rm A$まわりの力のモーメントのつり合いの式
$\dfrac{r}{\tan\theta}\cdot R=\dfrac{l}{2}\cos\theta\cdot mg$ $\dots (3\ast)$ (答)
(3) $(3\ast)$より
$\dfrac{r\cancel{\cos\theta}}{\sin\theta}\cdot R=\dfrac{l}{2}\cancel{\cos\theta}\cdot mg$
$\therefore R=\dfrac{l\sin\theta}{2r}mg$ (答) $\dots (4\ast)$
$(4\ast)$を$(\ast)$に代入して
$\eqalign{f&=R\sin\theta\\&=\dfrac{l\sin^{2}\theta}{2r}mg}$ (答)
$(4\ast)$を$(2\ast)$に代入して
$\eqalign{N&=mg-R\cos\theta\\&=mg-\dfrac{l\sin\theta}{2r}mg\cdot \cos\theta\\&=\left(1-\dfrac{l\sin\theta\cos\theta}{2r}\right)mg}$ (答)

コメント