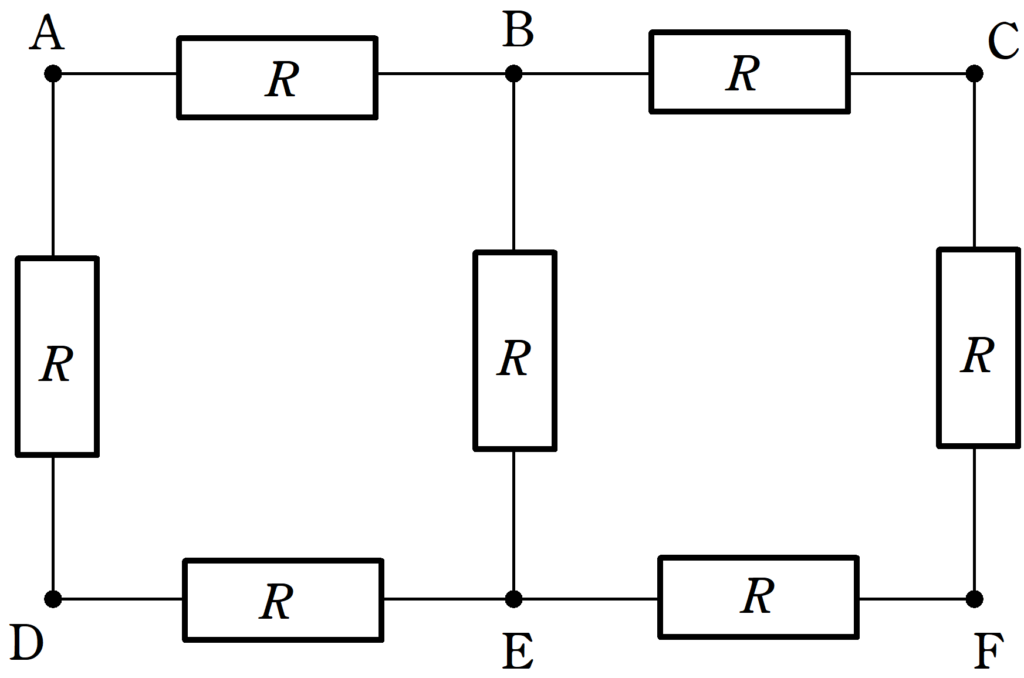
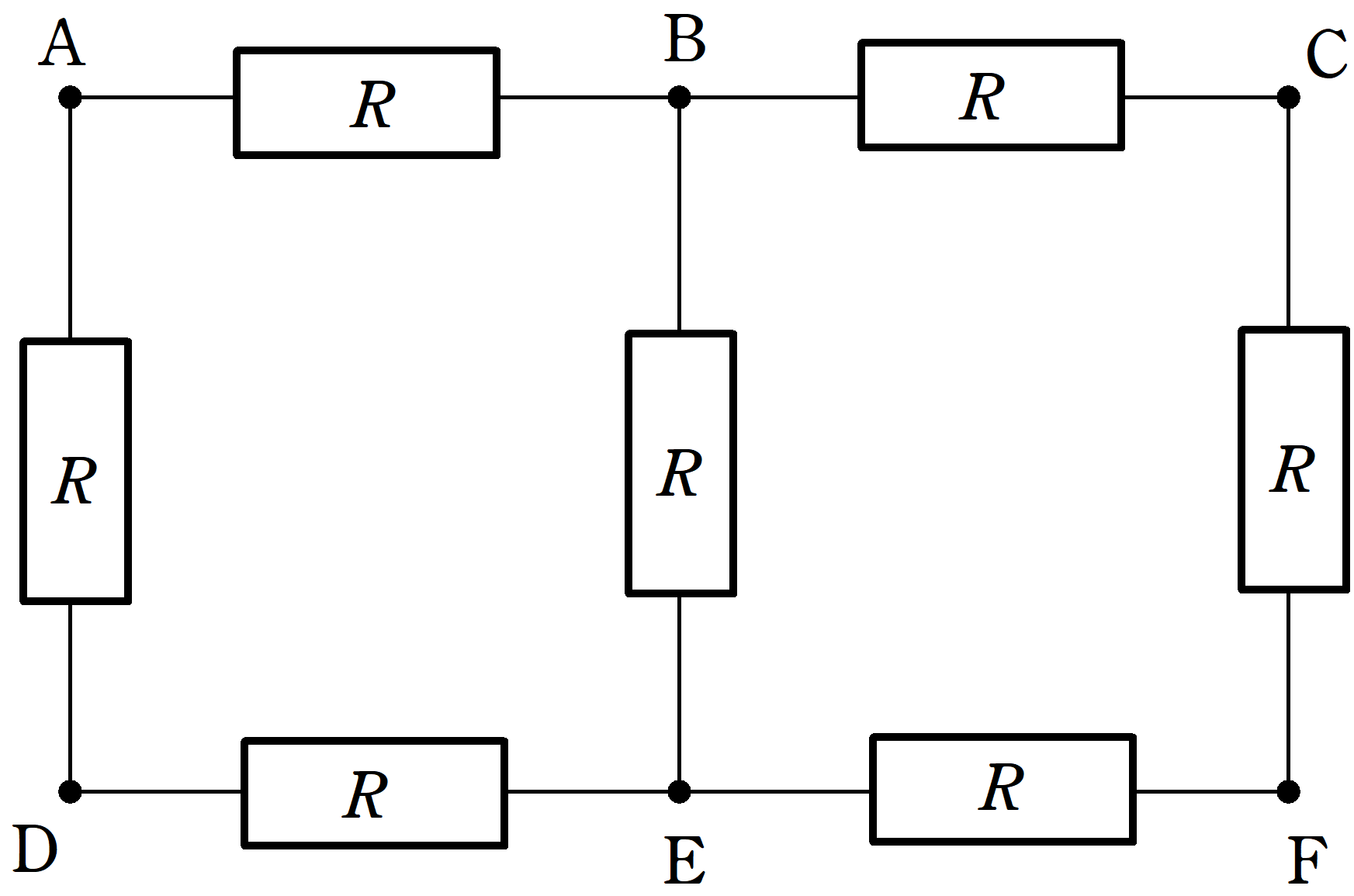
抵抗値$R$の7つの電気抵抗を上図のように,抵抗の無視できる導線で結んだ.
(1) BE間の合成抵抗を求めよ.
(2) DF間の合成抵抗を求めよ.
(3) AF間の合成抵抗を求めよ.
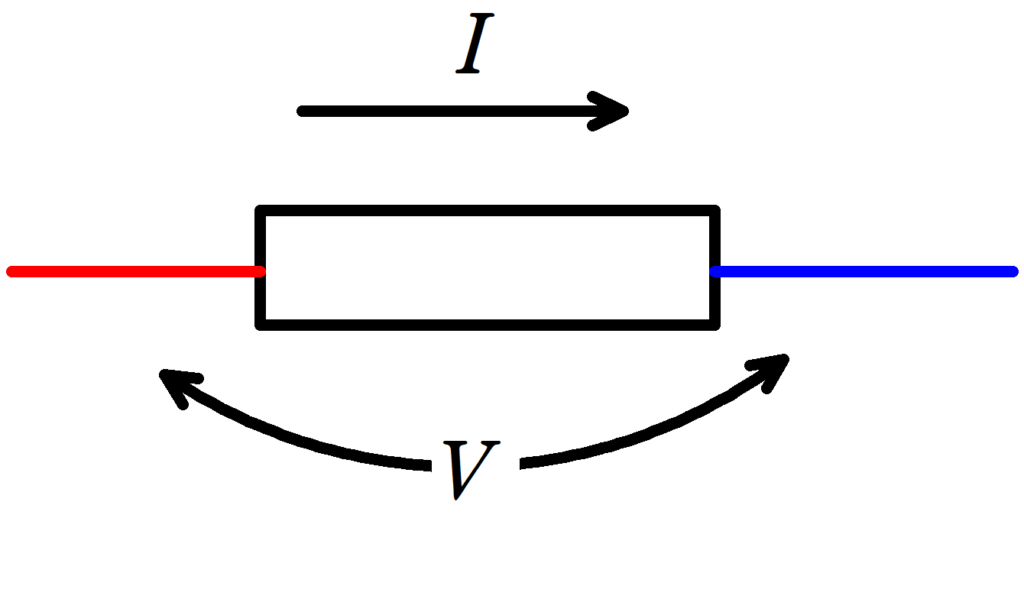
抵抗に流れる電流が$I$,電圧を$V$,抵抗値を$R$とするとき,
$V=RI$
が成り立つ.
合成抵抗を求めるときは,$\dfrac{V}{I}$を計算する.
(1)
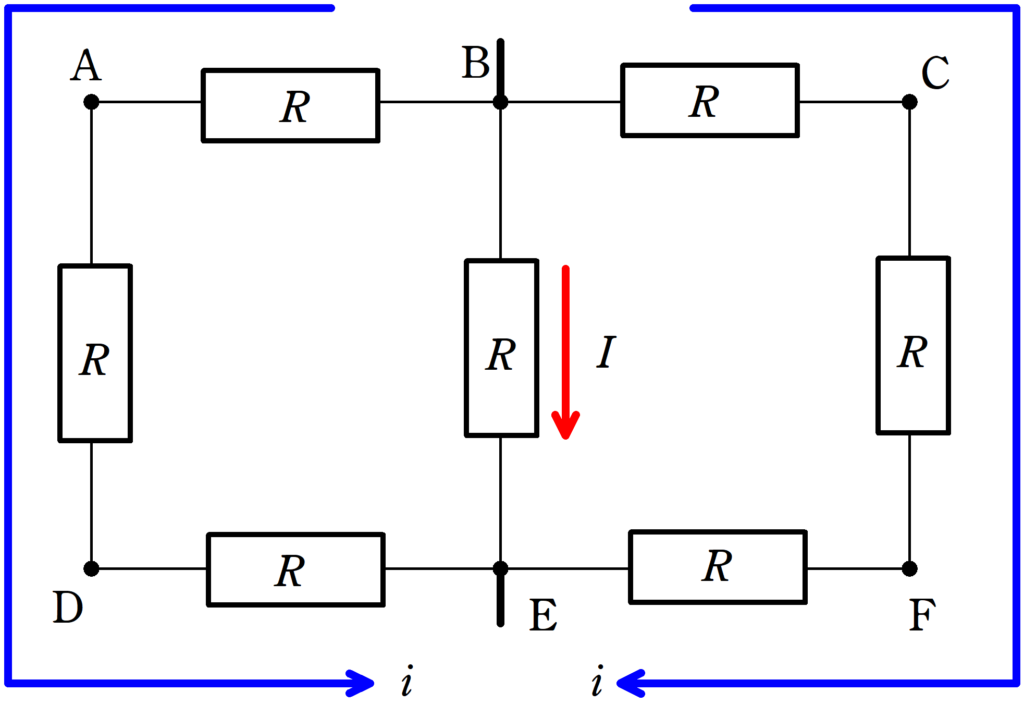

Bから電流を流し,Eから電流が流れ出るときについてです.
対称性から,B→A→D→Eに流れる電流と,B→C→F→Eに流れる電流は同じ$i$としましょう.
また,B→Eに流れる電流を$I$とします.
Eの電位を0,Bの電位を$V$として,BE間の合成抵抗は$\dfrac{V}{2i+I}$です.
キルヒホッフ則を立てましょう.
★ B→A→D→Eのキルヒホッフ則
$V-3Ri=0$
$\therefore i=\dfrac{V}{3R}$ $\dots (\ast)$
★ B→Eのキルヒホッフ則
$V-RI=0$
$\therefore I=\dfrac{V}{R}$ $\dots (2\ast)$
$(\ast),(2\ast)$より
$\eqalign{2i+I&=\dfrac{2V}{3R}+\dfrac{V}{R}\\&=\dfrac{5V}{3R}}$
したがって,
$\dfrac{V}{2i+I}=\dfrac{3}{5}R$ (答)

勿論,$3R$,$R$,$3R$の並列合成の式を用いてもよいです.
(2)
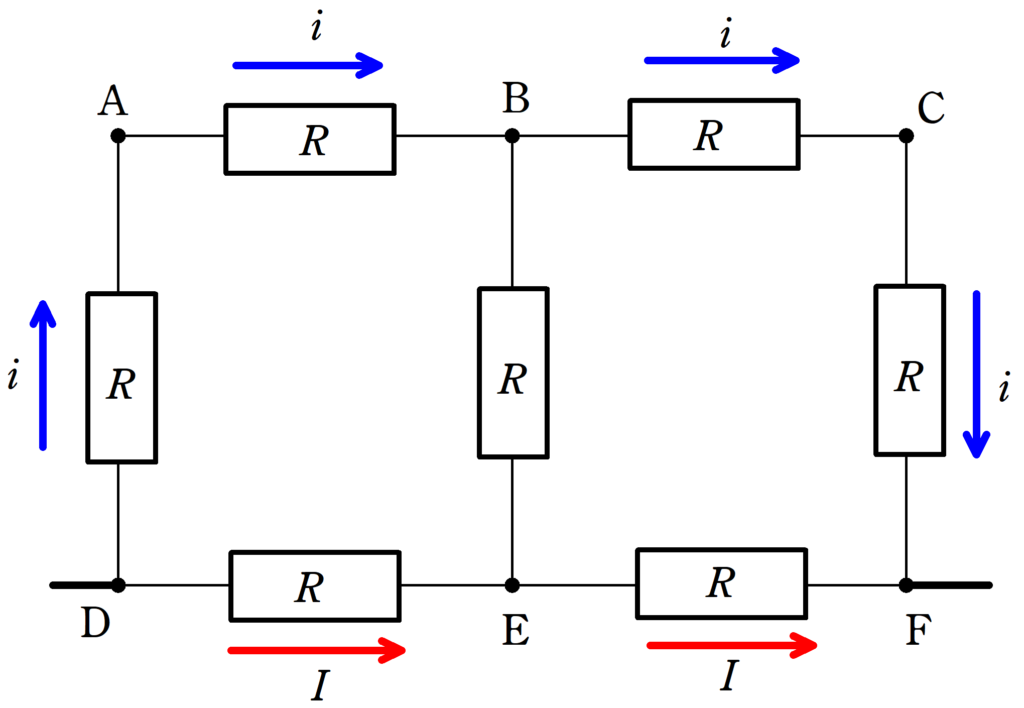

Dから電流が流れ込み,Fから電流がでていくことを考えます.
D→A→Bに流れる電流を$i$,D→Eに流れる電流を$I$とすると,対称性より,B→C→Fに流れる電流が$i$,E→Fに流れる電流が$I$となります.
その結果,BE間には電流が流れません.
Fの電位を0,Dの電位を$V$として,キルヒホッフ則を立てます.
合成抵抗は,$\dfrac{V}{i+I}$となります.
★ D→A→B→C→Fのキルヒホッフ則
$V-4Ri=0$
$\therefore i=\dfrac{V}{4R}$ $\dots (3\ast)$
★ D→E→Fのキルヒホッフ則
$V-2RI=0$
$\therefore I=\dfrac{V}{2R}$ $\dots (4\ast)$
$(3\ast)$,$(4\ast)$より
$\eqalign{i+I&=\dfrac{V}{4R}+\dfrac{V}{2R}\\&=\dfrac{3V}{4R}}$
したがって
$\dfrac{V}{i+I}=\dfrac{4}{3}R$ (答)
(3)
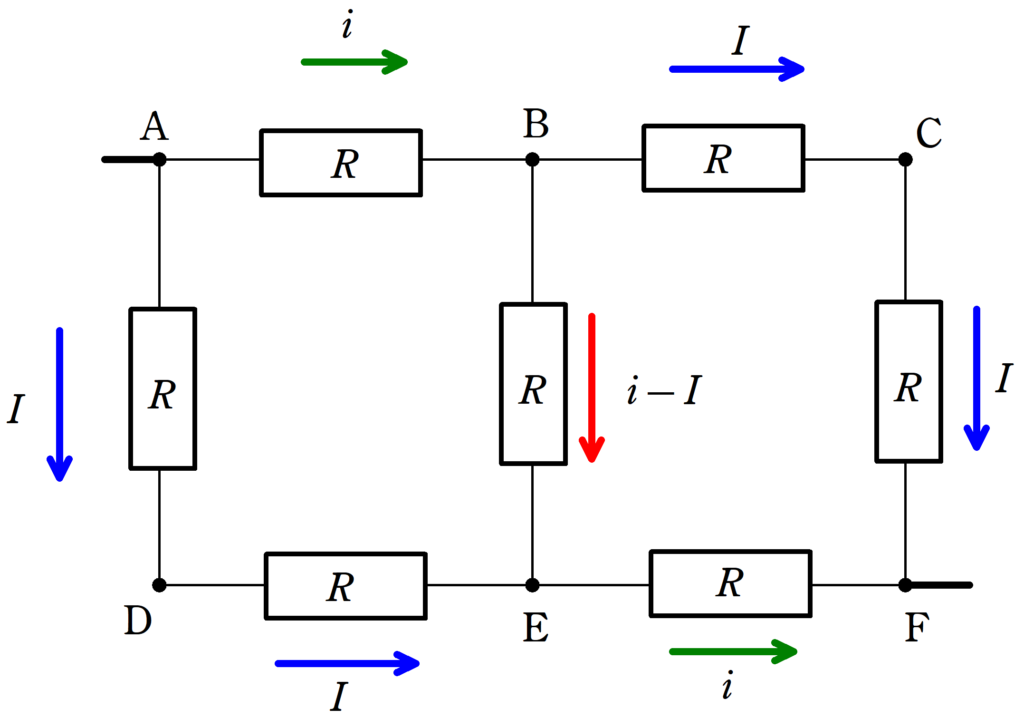

Aから電流が流れ込み,Fから電流がでていくことを考えます.
A→Bに流れる電流を$i$,A→D→Eに流れる電流を$I$とすると,対称性より,B→C→Fに流れる電流が$I$,E→Fに流れる電流が$i$となります.
すると,キルヒホッフ第1法則より,BE間に流れる電流は,$i-I$となります.
Fの電位を0,Aの電位を$V$として,キルヒホッフ則を立てます.
合成抵抗は,$\dfrac{V}{i+I}$となります.
★ A→B→C→Fのキルヒホッフ則
$V-Ri-2RI=0$
$\therefore i+2I=\dfrac{V}{R}$ $\dots (5\ast)$
★ A→B→E→Fのキルヒホッフ則
$V-Ri-R(i-I)-Ri=0$
$\therefore 3i-I=\dfrac{V}{R}$ $\dots (6\ast)$
$(5\ast)$,$(6\ast)$より,
$i=\dfrac{3V}{7R}$,$I=\dfrac{2V}{7R}$
したがって,合成抵抗は
$\dfrac{V}{i+I}=\dfrac{7}{5}R$ (答)

コメント
(3)の問題
3i+I=V/Rではなく、3i−I=V/Rではないでしょうか?
ご指摘ありがとうございます.
訂正します.