
波の式といえば,多くの人が嫌がるところなのではないでしょうか.
そもそも
$y=A\sin \{2\pi (\dfrac{t}{T}-\dfrac{x}{\lambda})\}$ $\dots (\ast)$

の式は何を意味しているのかわかりにくいですし,問題によって少し形が違うこともあります.
そこで,今回はこの波の式について解説を行っていきます.
この記事を読むと次のことがわかるようになります.
- 波がどのように伝わるかを理解できる.
- $(\ast)$の式の意味がわかる.
- 波の式を暗記ではなく,理解して式を立てることができる.

必ず確認しておいてほしいことがあります.
それは,
“波動とは媒質の振動が伝わる現象”
ということです.
そもそもここがわかっていないと波の式を立てることができません.
まずは“波動とは媒質の振動が伝わる現象”について確認しておきましょう.
波動は媒質の振動が伝わる現象

媒質とは,振動を伝える物質です.
たとえば,音であれば空気が媒質となり,地震であれば土や岩などです.
光は電場と磁場が相互に振動するのですが,ここでは話がややこしくなるので,光以外の波を考えていきましょう.
そして,今回は,波の中でも一番よく出てくる正弦波を考えます.(だからといって,すべての波が正弦波ではないことに注意してください.)
正弦波ができるのは,媒質が単振動するときです.
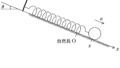
たとえば,下図のように$\rm{A_{0}}$~$\rm{A_{12}}$の媒質が等間隔に並んでいます.
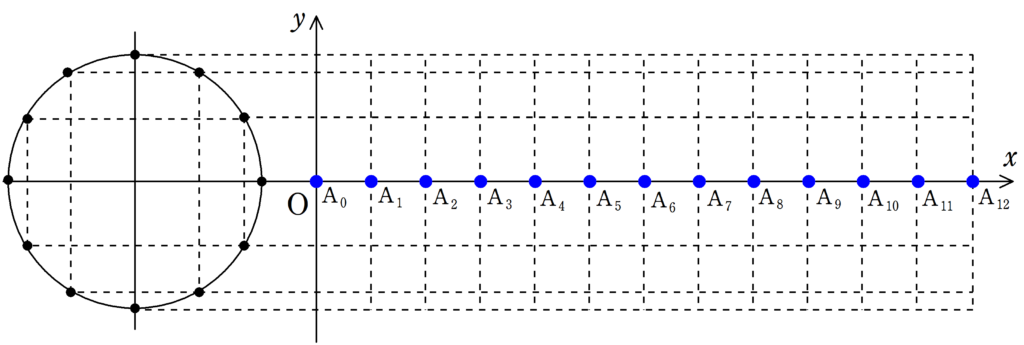

そして,$\rm{A_{0}}$の媒質に外力を加えて単振動させます.
単振動は等速円運動する物体に$y$軸に垂直な光を当てたときの,$y$軸に映った影の運動です.
単振動が何かわからない人は下の記事を読んでみてください.

いま,媒質$\rm{A_{0}}$~$\rm{A_{12}}$の媒質は相互作用をしていて,$\rm{A_{0}}$が単振動すると,$\rm{A_{1}}$も遅れて単振動をはじめます.
さらに,$\rm{A_{1}}$が単振動するとやはり遅れて$\rm{A_{2}}$も単振動をはじめます.
このように,それぞれの媒質は左隣りの媒質の影響で遅れて単振動します.
すると何が起こるのかをみていきましょう.
まずは,下の12個の図について,$\rm{A_{0}}$が単振動しているか確認してみてください.
さらに,$\rm{A_{1}}$,$\rm{A_{2}}$もそれぞれ遅れて単振動をしていることを確認してみましょう.
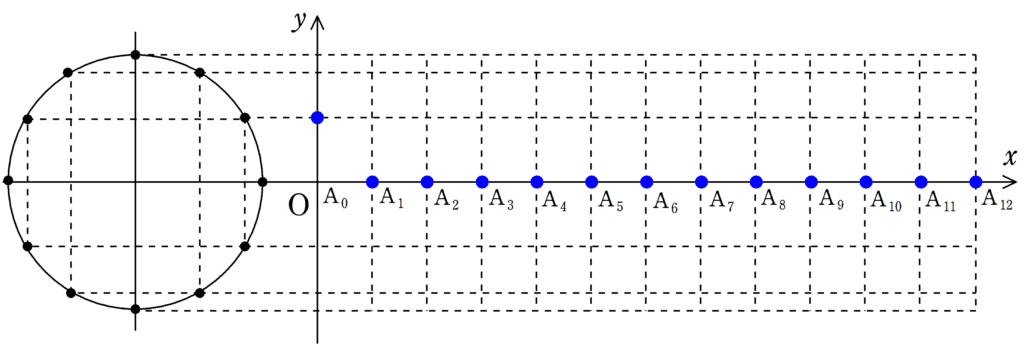
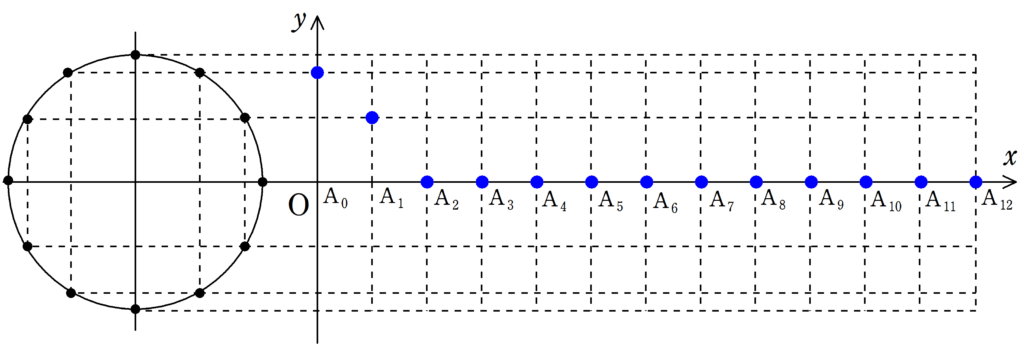
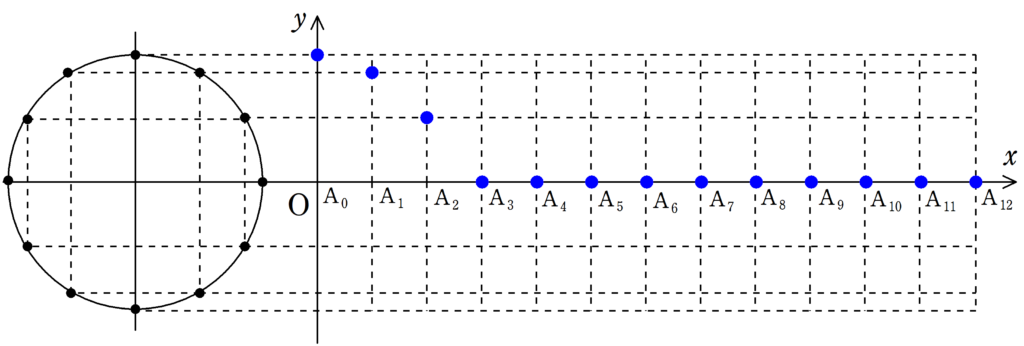
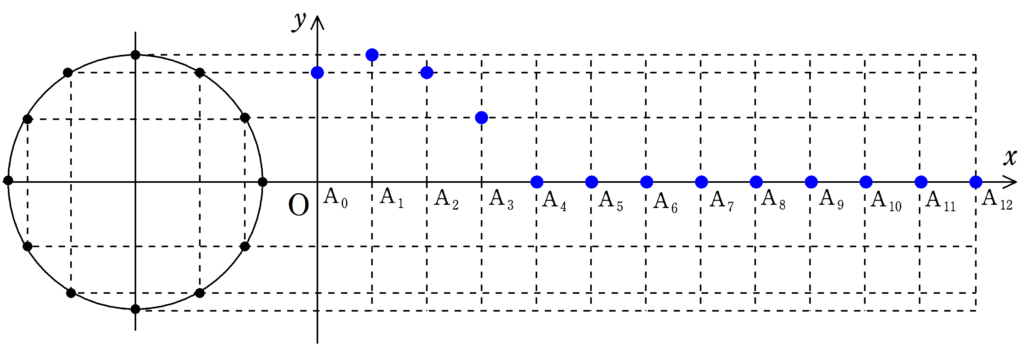
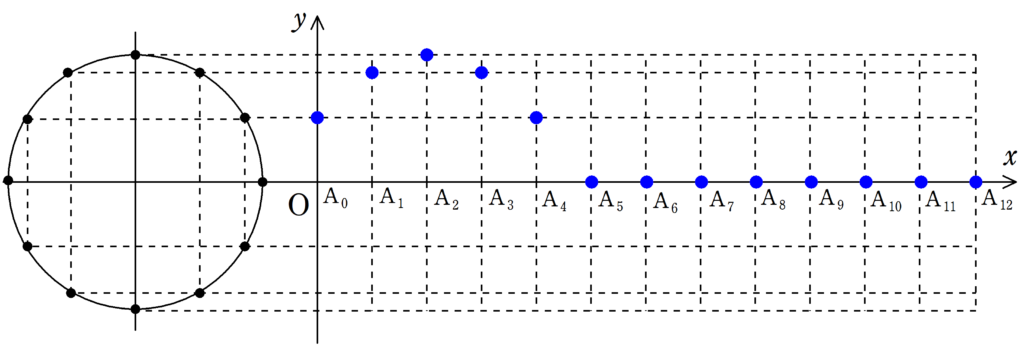
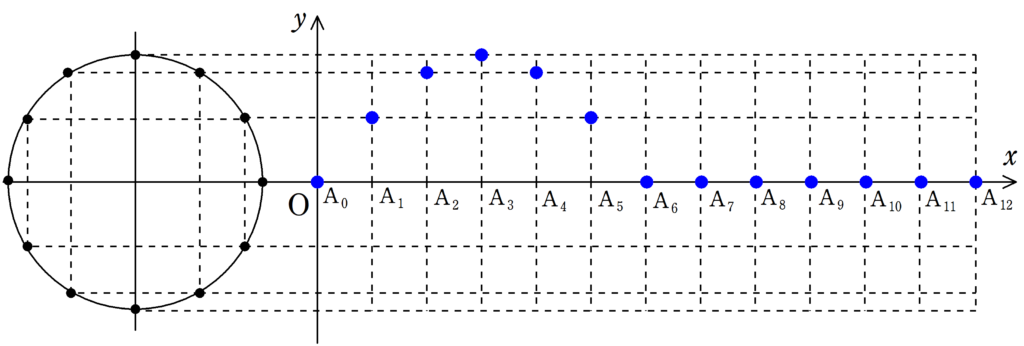
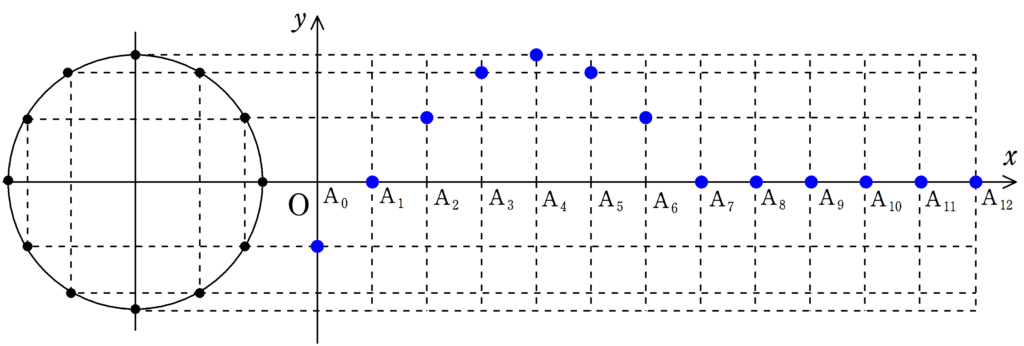
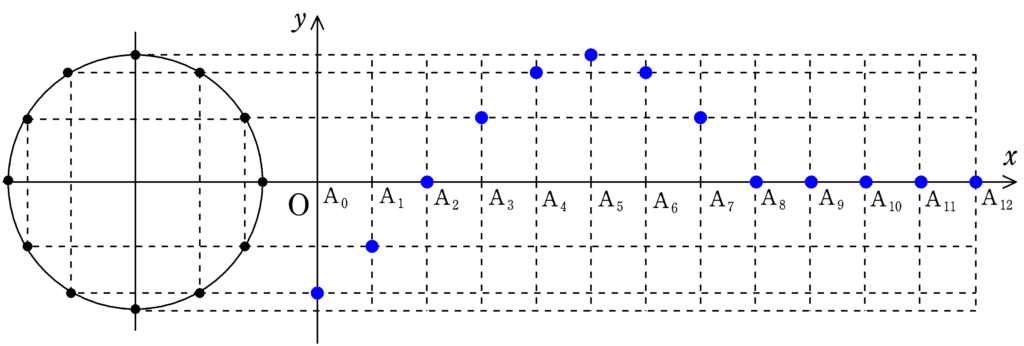
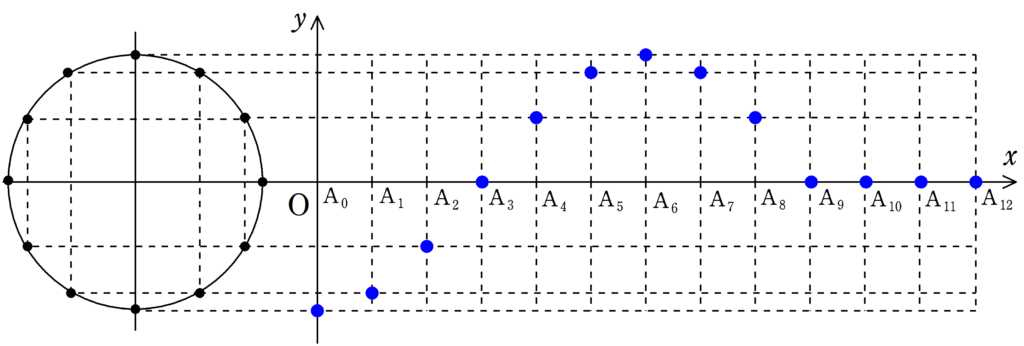
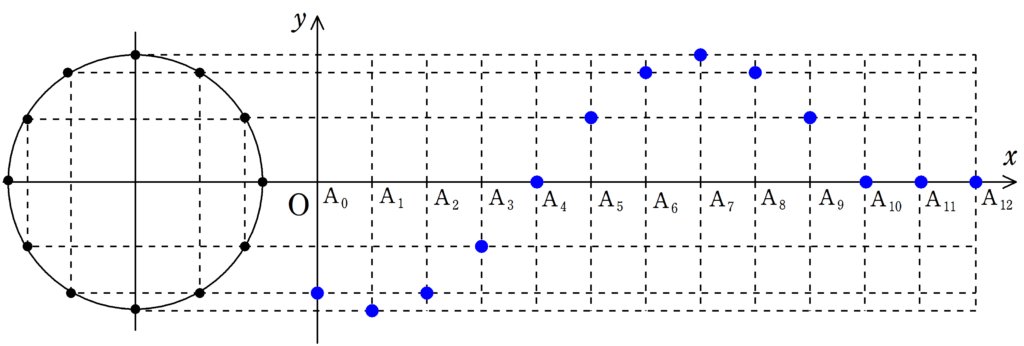
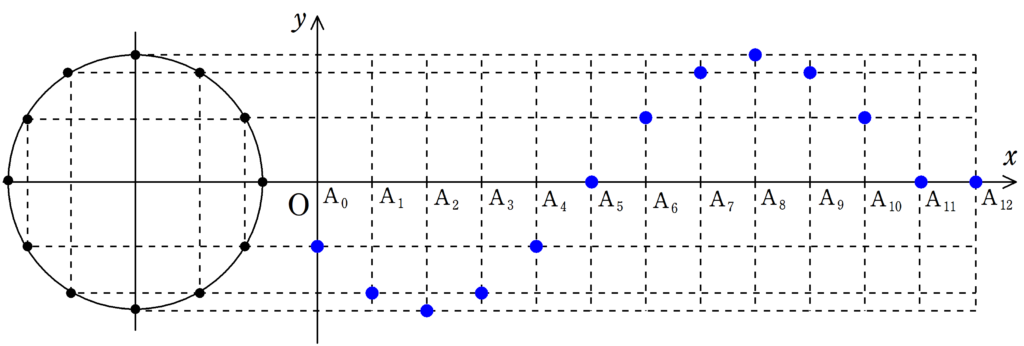
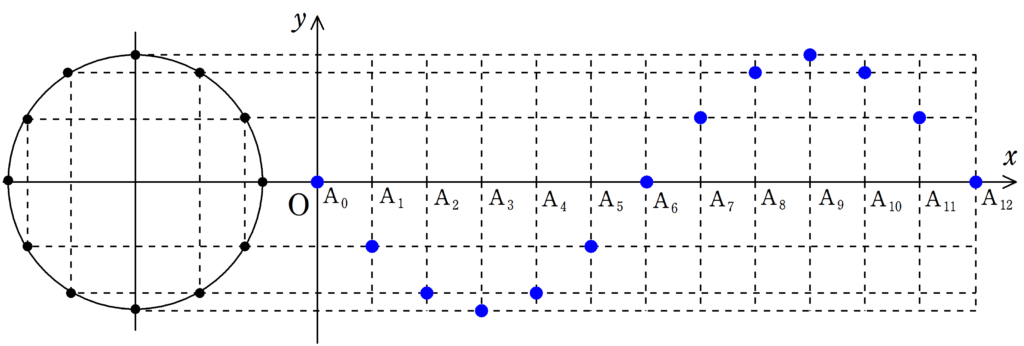

さて,確認してもらった通り,それぞれの媒質は単振動をしているだけです.
はじめに言ったように,波動とは振動が伝わる現象です.
$\rm{A_{0}}$が1回振動すると,上図のように,皆さんがよくしっている波1個分が出来上がっています.
$\rm{A_{9}}$のところは一番高いところで,ここを山といい,$\rm{A_{3}}$のところは一番低いところで,ここを谷といいます.
そして,$\rm{A_{0}}$から$\rm{A_{12}}$の長さを波長と言います.
波長は$\lambda$(ラムダ)と表すことが多いですね.
$\rm{A_{0}}$が1回振動した時間(周期$T$)で波が$\lambda$進んだので,波が伝わる速さ$v$は
$v=\dfrac{\lambda}{T}$

となります.これを波の基本式といいます.
おおげさな名前ですが,ただ単に距離と速さと時間の関係式です.
“波動とは,媒質の振動が伝わる現象”ということが理解できたでしょうか.
媒質が遅れて単振動をする


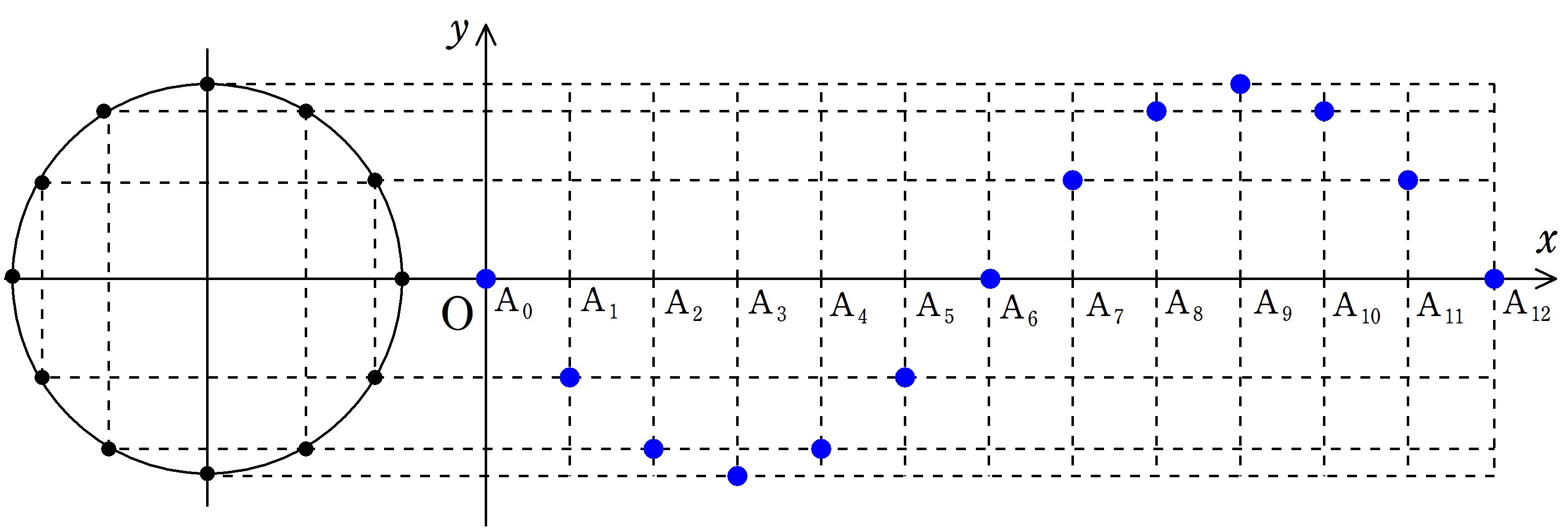
上図をみてください.
$x$軸上に青の媒質と緑の媒質があります.
この間にも媒質はありますが,省略しています.
青の媒質を単振動させましょう.青の媒質の時間変化$y_{青}$を振幅$A$,周期$T$,時刻$t$を用いて
$y_{青}=A\sin\dfrac{2\pi}{T}t$ $\dots (2\ast)$

とします.
このとき,座標$x$で振動している単振動の式はどのようになるでしょう?(もちろん,振動が伝わった後の振動の式です)
さきほど,”波動とは媒質の振動が伝えられる現象”であるということを確認しました.
しかも,その振動は遅れて伝わっていきます.
たとえば,青の媒質の振動が$3$秒かけて緑の媒質に伝わったとしましょう.
このとき,緑の媒質は3秒前の青の媒質と同じ振動をしていることになります.
たとえば,波がつくられるプールを思い浮かべましょう.
あの波は単振動とは違いますが,あくまでもイメージです.
波作成装置でつくられた場所での波の振動を遠くで見ていたあなたは,数秒後にあの波がきて自分自身も同じ振動をするんだなと思うでしょう.
つまり
青の媒質の振動が緑の媒質に伝わる時間を$\tau$とするとき,
緑の媒質の振動は時間$\tau$前の青の媒質の振動と同じ $\dots (\clubsuit)$

といえます.これで緑の媒質の振動がわかりますね.
波が伝わる速さを$v$とすれば,青の媒質と緑の媒質の距離は$x$なので,青の媒質の振動が緑の媒質に伝わる時間は$\dfrac{x}{v}$です.
$(2\ast)$と$(\clubsuit)$より,緑の媒質の振動の式$y_{緑}$は
$y_{緑}=A\sin\{\dfrac{2\pi}{T}(t-\dfrac{x}{v})\}$

さらにこの式を変形しましょう.波の基本式$v=\dfrac{\lambda}{T}$を変形して,
$vT=\lambda$より
$\eqalign{y_{緑} &= A\sin\{2\pi (\dfrac{t}{T}-\dfrac{x}{vT})\}\\&= A\sin\{2\pi(\dfrac{t}{T}-\dfrac{x}{\lambda})\}}$ $\dots (3\ast)$

$(3\ast)$の式を波の式と呼んでいます.
つまり,波の式とは位置$x$における媒質の振動の式ということです.
式の意味がわかり,10題ほど演習問題をすれば,なんてことありません.
しかし,なんとなくそうなんだー.
くらいでおわると意味はありません.
物理は必ず演習問題を解いて,理解を深めてください.
まとめ
- 波動とは,媒質の振動が伝わる現象である.
- 青の媒質の振動が緑の媒質に伝わる時間を$\tau$とすると,緑の媒質の振動は時間$\tau$前の青の媒質の振動と等しい
- 上の関係を使って,波の式を立てることできる.
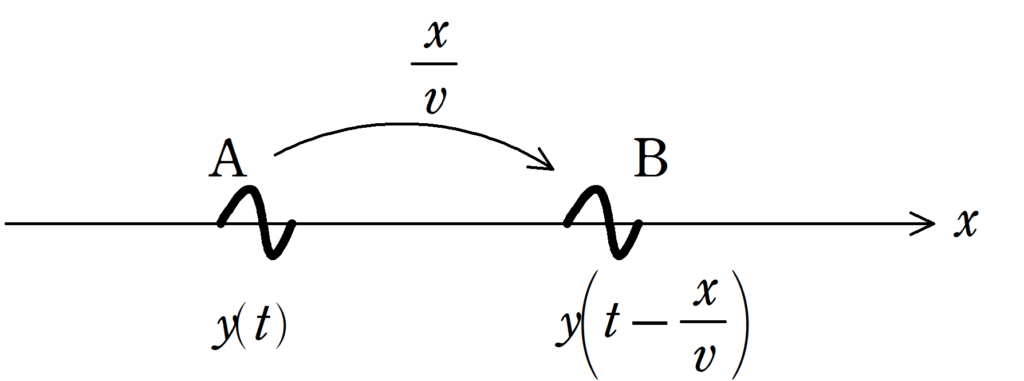
Aにおいて,媒質が単振動していて,その振動は$y_{\rm{A}}(t)$である.
波が伝わる速さが$v$でAからBの向きに波が伝わっているとする.
AB間の距離を$x$とすると,Aの振動がBの場所に伝えられるのにかかる時間は$\dfrac{x}{v}$である.
すると,Bの振動$y_{\rm{B}}(t)$は時間$\dfrac{x}{v}$前のAの振動と等しいので
$y_{\rm{B}}(t)=y_{\rm{A}}(t-\dfrac{x}{v})$

少し発展的だけど,
波の式の演習問題はこちらからどうぞ!



コメント
[…] [暗記するだけでは×]波の式を立てる波の式といえば,多くの人が嫌がると… PHYさん […]
[…] [暗記するだけでは×]波の式を立てるPHYさん波の式といえば,多くの人が嫌… 問題 […]
[…] [暗記するだけでは×]波の式を立てるPHYさん波の式といえば,多くの人が嫌… [演習問題]波の式を立てる.$y(0 ,t)$から$y(x , t)$の式へNEKO下の記事にある波の式の演習問題をやりたいな.入試でもよく出てくるし・・・PHYさんそうですね.それでは,波の式を立て方を上の記事を読んで復習しておいてください.あと,自由端反射と固…physicmath.net2020.09.29 PHYさん […]
[…] [暗記するだけでは×]波の式を立てるPHYさん波の式といえば,多くの人が嫌… […]
[…] [暗記するだけでは×]波の式を立てるPHYさん波の式といえば,多くの人が嫌… PHYさん […]
[…] [暗記するだけでは×]波の式を立てる […]