
前回の内容はこちらです.
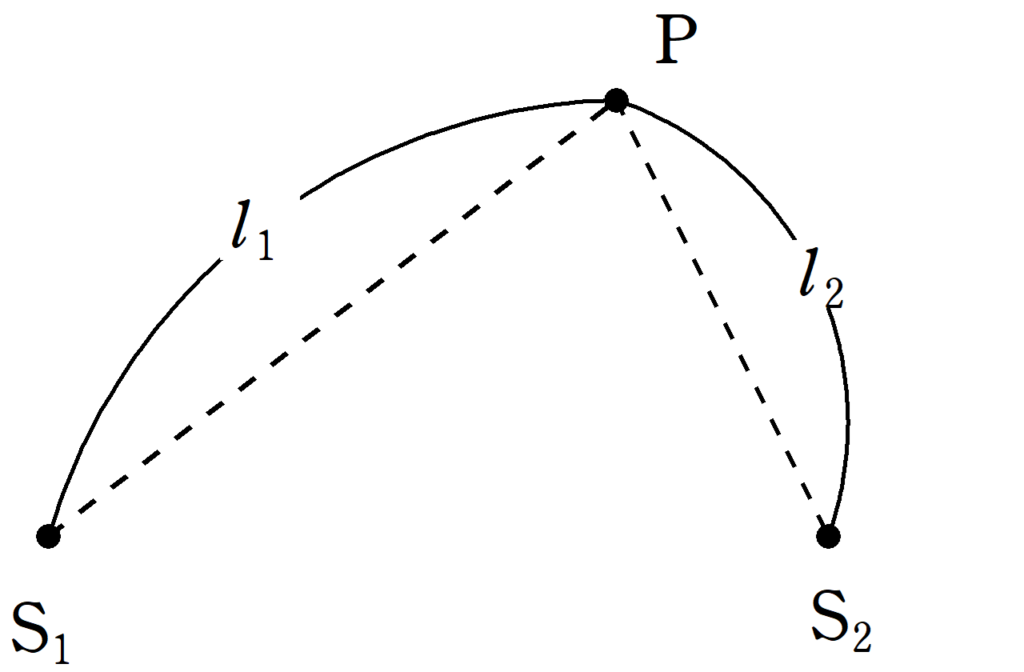
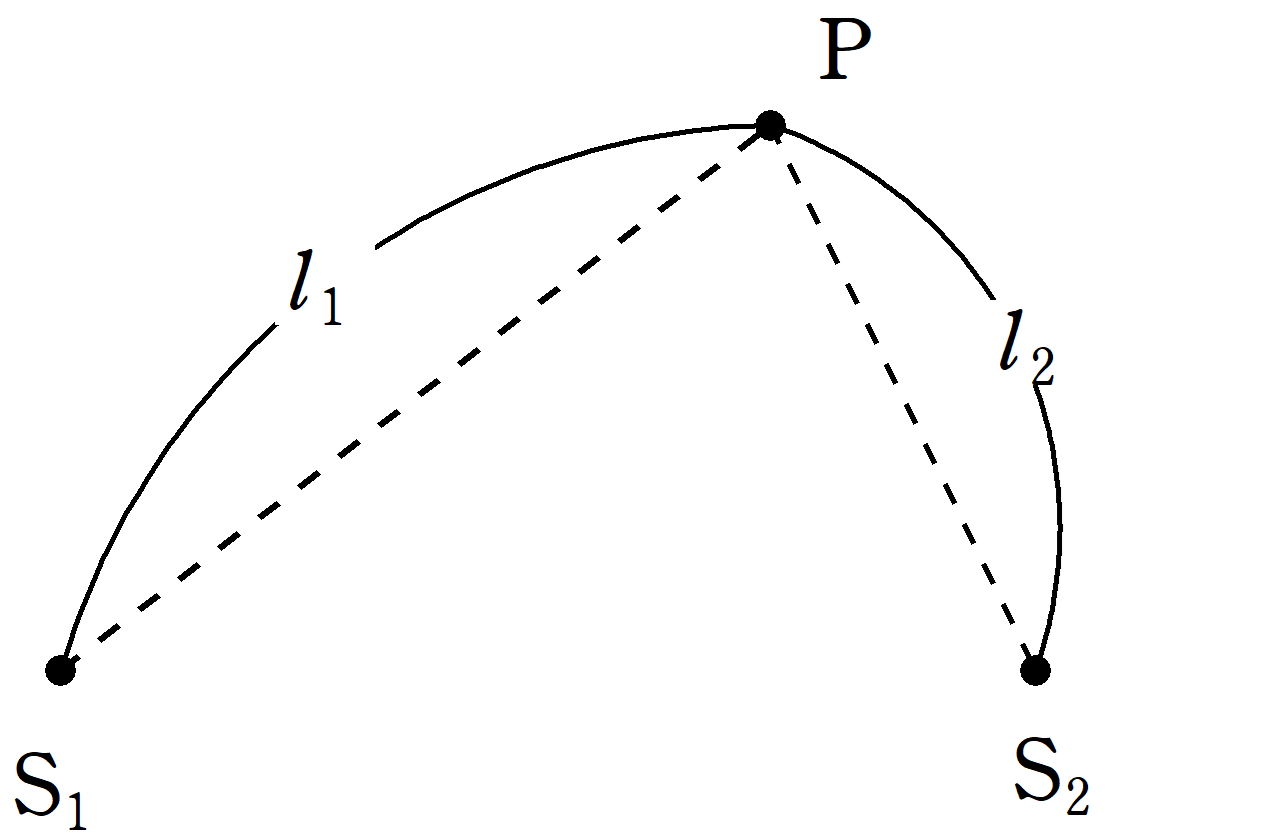
波源$\rm S_{1}$,$\rm S_{2}$があり,波源$\rm S_{1}$では時刻$t$において,$y_{1}=A\sin\left(2\pi ft\right)$で振動していて,波源$\rm S_{2}$では,$y_{2}=A\sin\left(2\pi ft\right)$で振動している.ただし,$A$は振幅,$f$は振動数であり,どちらも正の定数である.${\rm S_{1}P}=l_{1}$,${\rm S_{2}P}=l_{2}$であるような点$\rm P$がある.このとき,次の問いに答えよ.ただし,$\rm S_{1}P$の経路の媒質と$\rm S_{2}P$の経路の媒質は異なり,それぞれの波長が$\lambda_{1}$,$\lambda_{2}$である.
(1) $\rm S_{1}$から$\rm P$に伝わる波の$\rm P$における媒質の変位と$\rm S_{2}$から$\rm P$に伝わる波の$\rm P$における媒質の変位の位相差$\varDelta \varphi$を$\lambda_{1}$,$\lambda_{2}$,$l_{1}$,$l_{2}$を用いて表せ.
(2) 2つの波が強め合うときの条件を整数$k$および,$l_{1}$,$l_{2}$,$\lambda_{1}$,$\lambda_{2}$を用いてかけ.
(3) 2つの波が弱め合うときの条件を整数$k$および,$l_{1}$,$l_{2}$,$\lambda_{1}$,$\lambda_{2}$を用いてかけ.
<解答>
(1)

波が伝わる速さを$V_{1}$とすると,$\rm S_{1}$から$\rm P$に伝わる波において,$\rm P$で媒質の変位は,時間$\dfrac{l_{1}}{V_{1}}$前の$\rm S_{1}$での振動と等しいんだよね.
したがって,媒質の変位$y_{1\rm P}$は
$y_{1\rm P}=A\sin\left\{2\pi f\left(t-\dfrac{l_{1}}{V_{1}}\right) \right\}$

このとき,位相$\varphi_{1}$は,波の基本式,$V_{1}=f\lambda_{1}$も用いると次のようになります.
$\varphi_{1}=2\pi f\left(t-\dfrac{l_{1}}{V_{1}}\right)=2\pi ft-\dfrac{2\pi }{\lambda_{1}}l_{1}$

同じように,$\rm S_{2}$から$\rm P$に伝わる波の$\rm P$における媒質の位相$\varphi_{2}$は,波が伝わる速さを$V_{2}$として,
$\varphi_{2}=2\pi f\left(t-\dfrac{l_{2}}{V_{2}}\right)=2\pi ft-\dfrac{2\pi }{\lambda_{2}}l_{2}$

したがって,位相差$\varDelta \varphi$は
$\varDelta \varphi=\varphi_{1}-\varphi_{2}=2\pi\left(\dfrac{l_{2}}{\lambda_{2}}-\dfrac{l_{1}}{\lambda_{1}}\right)$ (答)
(2)

強め合うのは,$\varDelta \varphi$が$2\pi$の整数倍になるときなので
$\varDelta \varphi=2\pi k$
$\therefore 2\pi\left(\dfrac{l_{2}}{\lambda_{2}}-\dfrac{l_{1}}{\lambda_{1}}\right)=2\pi k$ (答)

ちょっと変わった形ですが,これが強め合いの条件です.
(3)

弱め合うのは,$\varDelta \varphi$が$\pi$の奇数倍のときなので
$\varDelta \varphi=(2k-1)\pi$
$\therefore 2\pi\left(\dfrac{l_{2}}{\lambda_{2}}-\dfrac{l_{1}}{\lambda_{1}}\right)=(2k-1)\pi$ (答)

このように,位相差を考えれば,少し変わった形にも対応できます.
次回の内容はこちら


コメント
[…] […]
[…] […]