
重心不変の問題を扱います.
変位を使って重心不変の問題を解いていきましょう.
重心不変はこちらでも扱っています.

まず,重心とは何か?を確認していきます.
こちらの記事でも扱っていますので詳しく知りたい方は確認してみてください.
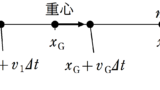
座標$x_{1}$,$x_{2}$にそれぞれ質量$m_{1}$,$m_{2}$の物体がある.
このときの重心の位置$x_{\rm G}$は
$x_{\rm G}=\dfrac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}$

さらに,重心速度や重心加速度も定義できます.
加速度$a_{1}$,$a_{2}$をもつ質量$m_{1}$,$m_{2}$の物体がある.
このときの重心加速度$a_{\rm G}$は
$a_{\rm G}=\dfrac{m_{1}a_{1}+m_{2}a_{2}}{m_{1}+m_{2}}$

ここから次のように変形して,重心の運動方程式を作ります.
質量$m_{1}$,$m_{2}$の物体の重心の加速度を$a_{\rm G}$とする.2つの物体にはたらいている力をそれぞれ$F_{1}$,$F_{2}$とすると,次の式が成り立つ.
$(m_{1}+m_{2})a_{\rm G}=F_{1}+F_{2}$

これらを踏まえた上で,重心不変とはなにかを説明しましょう.
はじめ,重心が静止していて,その後,ある成分について力の和が0であるとき,その成分の重心は静止したままである.

要するに,はじめ重心が止まっていて,そこに力がはたらかないんだったら,重心は動かないで止まったままだよね,という話です.
それでは,重心不変の問題を解いていきましょう.
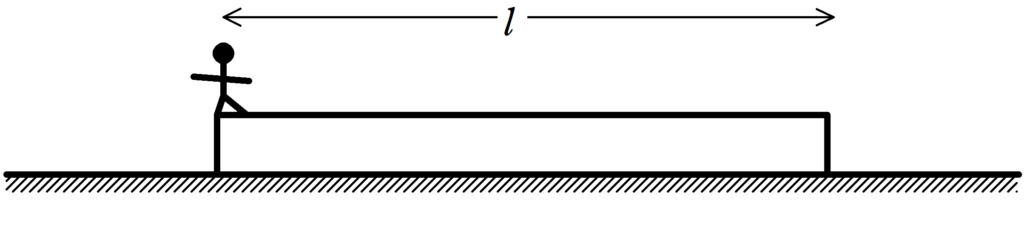
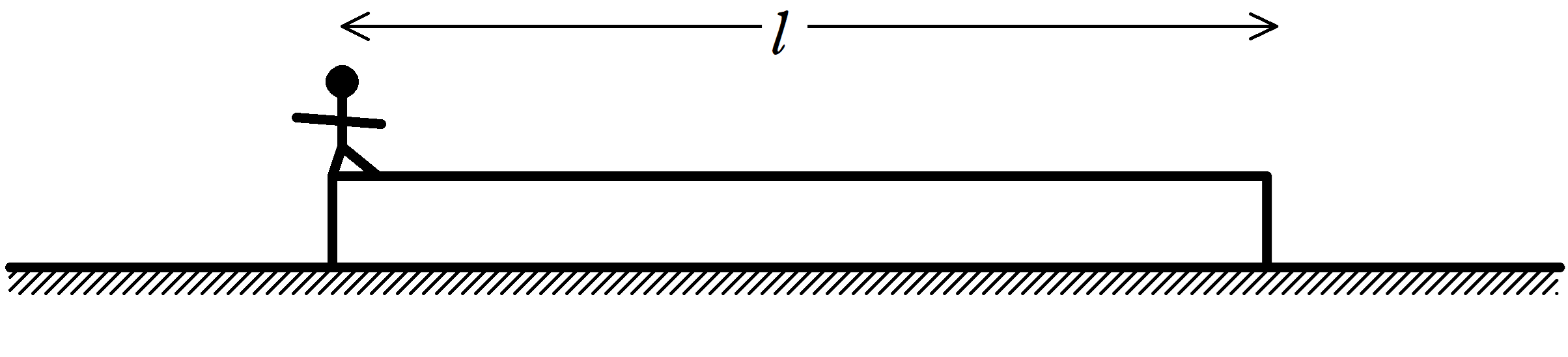
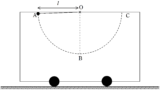
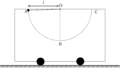
図のように,水平でなめらかな床の上になめらかで水平な上面をもつ長さ$l$の板が静止している.板の左端に人が静止して,ゆっくりと板の上を歩き,板の右端まで到達した.このとき,板と人は水平な床からみてどれだけ移動したか.ただし,板の質量を$M$,人の質量を$m$とする.
<解答>

人が板の上を歩くとき,板を蹴って進んでいます.このときに,水平方向にはたらく力の和が0になるので,重心が変化しませんね.
そこで,床から見た板の変位を$\varDelta X$,人の変位を$\varDelta x$とします.
変位とは,位置の変化分のことです.

変位を利用した重心不変は次の2式を立てましょう.
重心不変の条件を満たすとき,次の2式を立てる.
1. 重心不変の式,つまり,重心の変化が0である式を立てる.
2. 相対変位の式
★ 重心不変の式
重心変化は0なので
$0=\dfrac{M\varDelta X+m\varDelta x}{M+m}$
$\therefore \varDelta X=-\dfrac{m}{M}\varDelta x$ $\dots (\ast)$

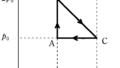
相対変位は,次のように図をかいて矢印を追うと簡単だね.
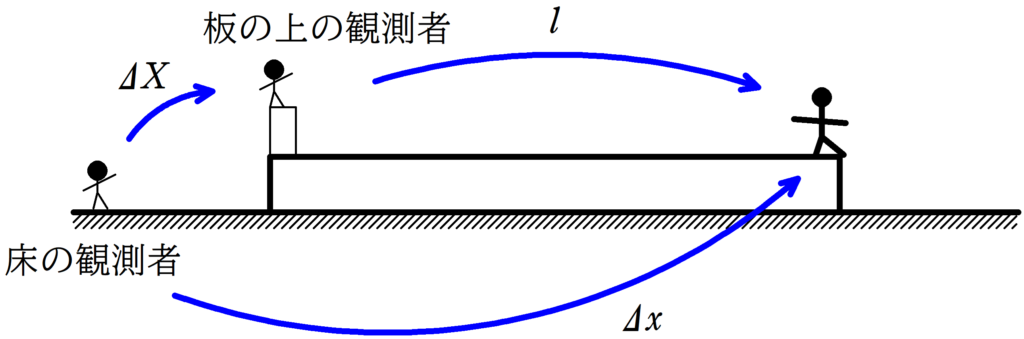
$\varDelta X+l=\varDelta x$ $\dots (2\ast)$
※ $l$は床からみて移動した距離ではなく,板から見て移動した距離です.
$(\ast)$,$(2\ast)$より$\varDelta X$を消去して$\varDelta x$を求めると
$\eqalign{-\dfrac{m}{M}\varDelta x+l&=\varDelta x\cr\left(1+\dfrac{m}{M}\right)\varDelta x&=l\cr \dfrac{M+m}{M}\varDelta x&=l\cr \varDelta x&=\dfrac{M}{M+m}l}$
さらに,$\varDelta x=\dfrac{M}{M+m}l$を$(\ast)$に代入して
$\varDelta X=-\dfrac{m}{M}\cdot \dfrac{M}{M+m}l=-\dfrac{m}{M+m}l$
以上から,人は床から見て図の右向きに,$\dfrac{M}{M+m}l$(答)移動し,板は図の左向きに$\dfrac{m}{M+m}l$だけ移動した.(答)

次回の内容はこちら.

コメント
[…] [演習]重心不変1NEKO重心不変の問題を扱います.変位を使って重心不変の問… 問題 […]
[…] [演習]重心不変1NEKO重心不変の問題を扱います.変位を使って重心不変の問… [演習]重心不変2NEKO今回も重心不変の問題です.前回の内容はこちら.問題図のように,水平でなめらかな床の上に質量m$の台車がある.台車の天井の中央Oに長さ$l$の軽い糸が結び付けられており,他端には質量$m…physicmath.net [演習]重心不変3PHYさん前回の内容はこちらです.問題図のように,水平でなめらかな床の上に質量$M_{3}$の三角台がおいてある.三角台の上面は傾角$theta$の斜面でできており,斜面はなめらかである.斜面の上には質…physicmath.net [演習]重心不変4PHYさん前回の内容はこちらです.問題図のように,水平でなめらかな床の上に質量$M$の台がおかれている.台の上面は,傾角$theta$で長さ$L$の斜面部分AB,長さ$l$の水平部分BC,半径$R$の曲…physicmath.net 分野別力学演習問題演習問題(標準)高校物理 シェアする Twitter Facebook はてブ LINE physicmathをフォローする physicmath Physicmath(フィジクマス) […]