
前回の内容はこちらです.
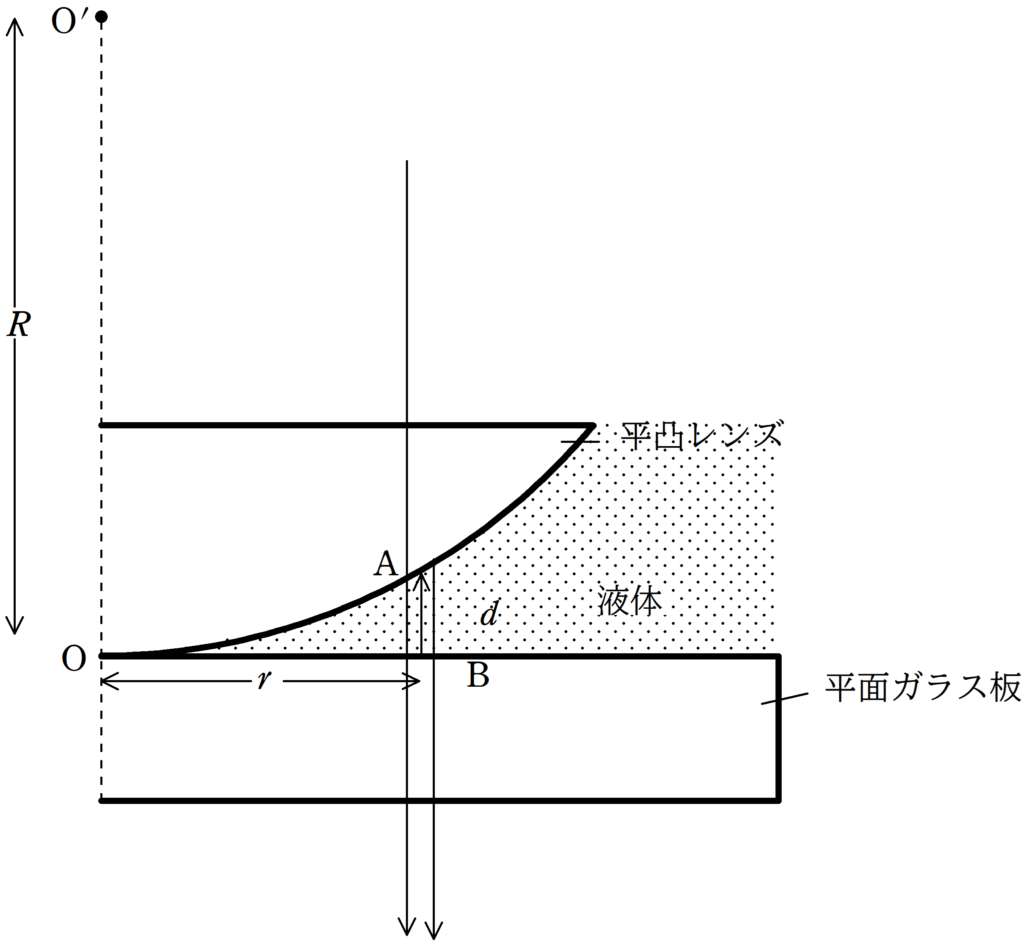
図のように,厚い平面ガラス板の上に平凸レンズを置く.レンズは中心の位置Oでガラス板と接触していて,ガラス板の平面とレンズの平面は平行になっている.また,ガラス板と平凸レンズの間には,空気に対する相対屈折率$n^{\prime}$の液体で満たされている.レンズの平面側の上方から波長$\lambda$の単色光を平面に直角に照射して,レンズの平凸レンズ側(図の下側)から眺める.すると,光の明暗の線が同心円状に交互に観測される.レンズの中心線からの距離を$r$,その位置でのレンズとガラス板の間の液体層の厚みを$d$とする.レンズの曲面は中心を$\rm O^{\prime}$とする曲率半径$R$の球面の一部とみなす.空気に対するレンズおよびガラス板の屈折率を$n$とし,$R$は,$r$に比べて十分大きいとする.照射した光の透過光とBにおいて反射し,再びAにおいて反射した光の干渉を考えるとして,次の問いに答えよ.
(1) $n^{\prime}>n>1$のとき,中心Oより$m$番目$(m=1 , 2 , \dots)$の明環のOからの距離$r$を$m$,$R$,$n$,$\lambda$を用いて表せ.
(2) $n^{\prime}>n>1$のとき,中心Oより$m$番目$(m=1 , 2 , \dots)$の暗環のOからの距離$r$を$m$,$R$,$n$,$\lambda$を用いて表せ.
(3) $n^{\prime}>n>1$のとき,中心付近は明るいか,暗いか.
<解答>
(1)

経路差は$2d=\dfrac{r^{2}}{R}$です.(こちらでで確認してください.)
また,Aを透過した光がBで自由端反射し,Aで再び自由端反射し,Bを透過するので,反射による位相のずれは0となります.
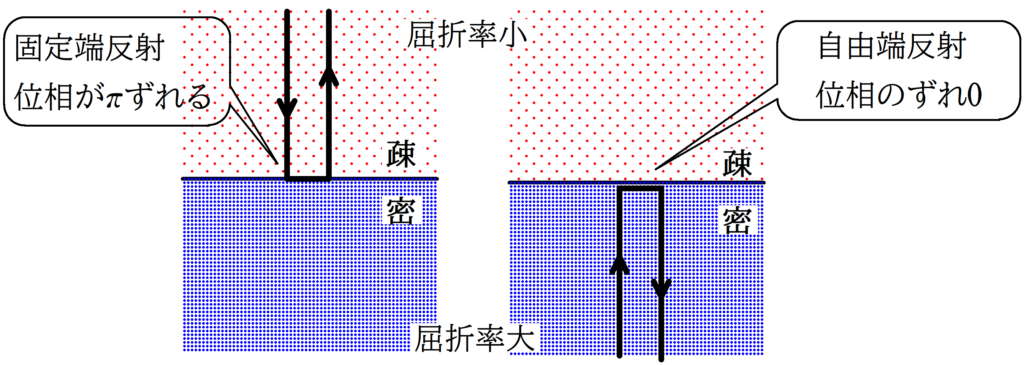
反射による位相のずれは次のことを覚えておきましょう.

また,位相差は次のことを確認しましょう.
地点Pにおける2つの波の位相差を$\phi$,整数を$m$とすると,
強め合いの条件:$\phi=2\pi m$
弱め合いの条件:$\phi=(2m+1)\pi $
位相差$\phi$は次の3つの要素で決まる.
$\phi_{1}$:初期位相のずれ
同位相なら$\phi_{1}=0$,逆位相なら$\phi_{1}=\pi$
$\phi_{2}$:反射による位相のずれ
自由端反射なら$\phi_{2}=0$,固定端反射なら$\phi_{2}=\pi$
$\phi_{3}$:距離の差(屈折率が変わることで生じる光学的な距離の差を含む)による位相のずれ
距離の差が$\Delta l$のとき,次の比例式を立てて,位相差$\phi_{3}$を計算する.
$2\pi : \lambda =\phi_{3} : \Delta l$
$\therefore \phi_{3}=\dfrac{2\pi}{\lambda}\Delta l$
このとき,位相差$\phi$は
$\phi=\phi_{1}+\phi_{2}+\phi_{3}$

2つの光の位相差$\varDelta \varphi$は次のようになります.
屈折率$n^{\prime}$での波長が$\dfrac{\lambda}{n^{\prime}}$であることに注意しましょう.
★ 位相差
$\eqalign{\varDelta\varphi&=\dfrac{2\pi}{\dfrac{\lambda}{n^{\prime}}}\cdot \dfrac{r^{2}}{R}\\&=\dfrac{2\pi n^{\prime}r^{2}}{R\lambda}}$

したがって,明環条件は次のようになります.
★ 明環条件
$\eqalign{\varDelta\varphi&=\pi \cdot 2(m-1)\\r&=\sqrt{\left(m-1\right)R\cdot \dfrac{\lambda}{n^{\prime}}}}$ (答)
(2)
★ 暗環条件
$\eqalign{\varDelta\varphi&=\pi \cdot (2m-1)\\r&=\sqrt{\left(m-\dfrac{1}{2}\right)R\cdot\dfrac{\lambda}{n^{\prime}}}}$ (答)
(3)

(1)において,$m=1$のとき,$r=0$であるから,中心O付近は明るく(答)なります.

上から見た場合と明暗が逆になります.


コメント