
今回は2つのばねがあるときの単振動の問題を扱います.いわゆる,ばね定数の合成を行うのですが,似ている形でも合成の仕方が全く違います.まずは,物体の両端にばねがついた問題です.
前回の記事はこちら
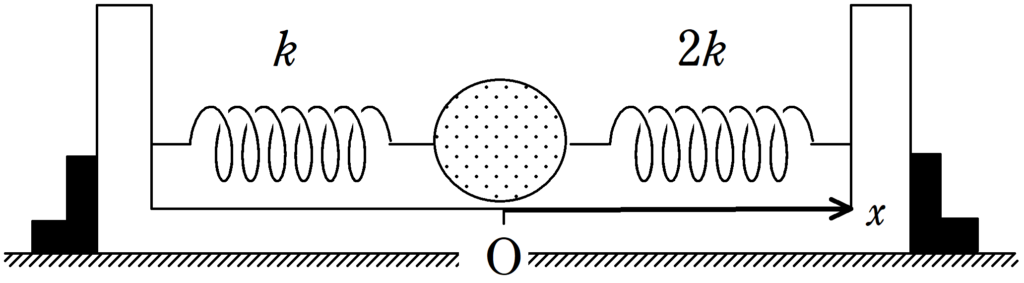
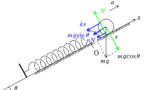
上図のように,水平な床に固定された箱があり.その内部に質量$m$の物体がおかれている.物体の左側にばね定数$k$のばねがついており,右側にばね定数$2k$のばねがつながれていて,それぞれの他端は箱にとりつけられている.はじめは左側と右側のばねはどちらも自然長であった.この場所を原点とし,左側のばねが伸びる方向に$x$軸をとる.外力を加え$x=l$までもっていき,静かに手をはなした後,物体は単振動をはじめた.次の問いに答えよ.ただし,ばねは軽く,物体と箱の内側部分の間には摩擦はないものとする.
(1) 振動の中心座標$x_{0}$,角振動数$\omega$,周期$T$を$k$,$m$から必要なものを用いて表せ.
(2) 物体が動き出した時刻を$t=0$とする.時刻$t$における物体の位置$x$を,$l$,$k$,$m$,$t$を用いて表せ.
<解答>
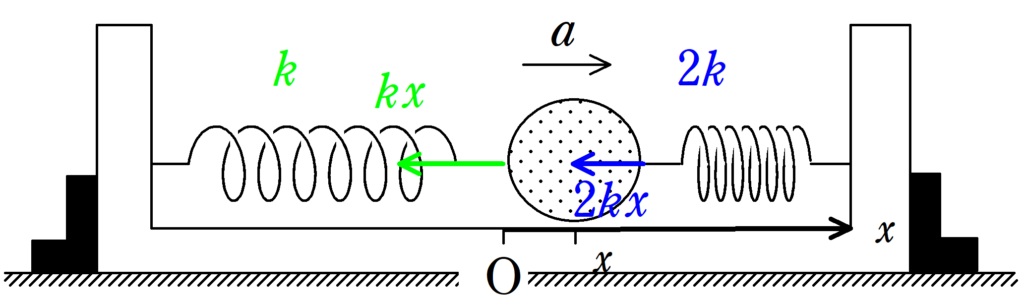
(1) 位置$x$における物体の加速度を$x$軸の正の向きに$a$と設定しましょう.上図のように,$x>0$のときを考えます.(前に調べたように,$x<0$でも同じ式になります.)左側のばねは伸びている状態なので,物体を自然長に戻すように引っ張り,その大きさは$kx$です.また,右側のばねは縮んている状態なので,ばねを物体を自然長に戻すように押し,その大きさは$2kx$です.どちらも左向きに力がかかっていますね.したがって,運動方程式は
$ma=-kx-2kx=-3kx$
この運動方程式から中心座標は$x_{0}=0$,角振動数は$\omega=\sqrt{\dfrac{3k}{m}}$,周期は$T=2\pi \sqrt{\dfrac{m}{3k}}$となります.
(2) 中心座標が$x_{0}=0$で$x=l$からスタートし,$x$軸の負の方向にいくので$\cos$型です.振幅は中心と右端である$x=l$との距離$A=l$ですね.
$x=A\cos \omega t=l\cos \sqrt{\dfrac{3k}{m}}t$
いままでの単振動の問題ができていれば,この問題もさほど難しくないと思います.合成ばね定数という考え方ではなく,いつも通りに力を図示すれば解くことができます.

それでは,次の問題です.
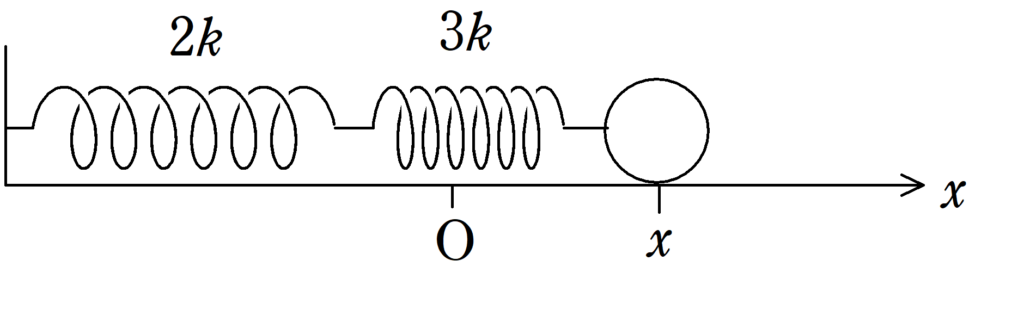
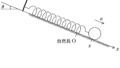
上図のように,ばね定数$2k$,$3k$の2つの軽いばねを直列につなげて,一端を物体に,他端を壁に固定した.物体は水平でなめらかな床の上にある.2つのばねが自然長にあるときの物体の位置を原点として,ばねが伸びる方向に$x$軸をとる.ばねを$x=l(l>0)$まで伸ばして静かに手をはなしたところ物体は単振動をした.このとき,次の問いに答えよ.
(1) 振動の中心座標$x_{0}$,角振動数$\omega$,周期$T$を$k$,$m$から必要なものを用いて表せ.
(2) 物体が動き出した時刻を$t=0$とする.時刻$t$における物体の位置$x$を,$l$,$k$,$m$,$t$を用いて表せ.
解答の前に,ばねを直列につなげたときにどのように考えていけばよいか考えていきましょう.
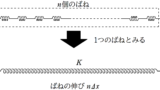
ばね定数$k_{1}$と$k_{2}$のばねを直列につなげる.このとき,合成ばね定数を$K$とすると,次の式が成り立つ.
$\dfrac{1}{K}=\dfrac{1}{k_{1}}+\dfrac{1}{k_{2}}$ $\dots (\clubsuit)$
理由は次の通りです.
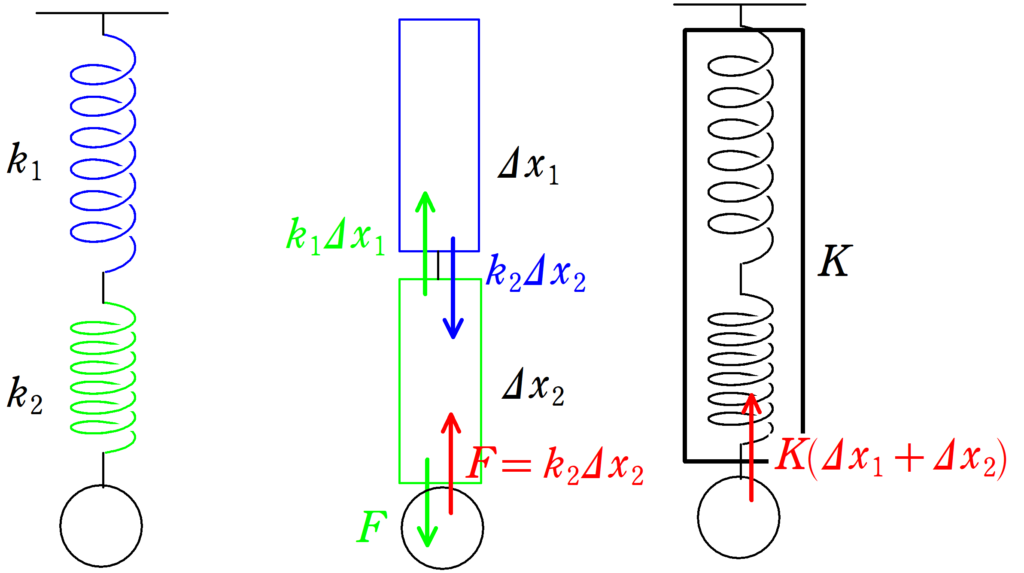
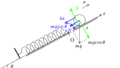
上図のようなばね定数$k_{1}$と$k_{2}$の軽いばねを考えましょう.軽いので$m\fallingdotseq 0$です.たとえば,それぞれのばねが$\Delta x_{1}$,$\Delta x_{2}$伸びているとき,物体は緑のばね(ばね定数$k_{2}$の方のばね)より鉛直上方向に力$F$の弾性力を受けます.これが運動方程式を立てる際に必要となる力ですね.$F=k_{2}\Delta x_{2} $です.また,緑のばねにはたらく力の合力は$0$と近似できます.理由は”軽いばね”だからです.質量$m$,加速度$a$,力$F$がはたらくとき
$ma=F$,$m=0$ のとき $F=0$
から,いくら加速度をもっていても質量が$0$であれば,力の和は$0$となります.したがって,緑のばねにはたらく力の合力が0になるためには,青いばね(ばね定数$k_{1}$の方のばね)が緑のばねを引く力$k_{1}\Delta x_{1}$と$k_{2}\Delta x_{2}$の大きさが等しくなります.
$k_{1}\Delta x_{1}=k_{2}\Delta x_{2}$
すなわち
$F=k_{1}\Delta x_{1}=k_{1}\Delta x_{2}$
これを変形して
$\Delta x_{1}=\dfrac{F}{k_{1}}$,$\Delta x_{2}=\dfrac{F}{k_{2}}$
$\therefore$ $\Delta x_{1}+\Delta x_{2}=\dfrac{F}{k_{1}}+\dfrac{F}{k_{2}}=\dfrac{k_{1}+k_{1}}{k_{1}k_{2}}F$
この式から$F$は
$F=\dfrac{k_{1}k_{2}}{k_{1}+k_{1}}(\Delta x_{1}+\Delta x_{2})$
ここで,$K=\dfrac{k_{1}k_{2}}{k_{1}+k_{1}}$とおくと,
$\dfrac{1}{K}=\dfrac{1}{k_{1}}+\dfrac{1}{k_{2}}$
となります.つまり,この合成ばね定数を使えば,物体にはたらく力の大きさ$F$は
(合成ばね定数)$\times$(2つのばねの伸びまた縮みの和)
と計算できます.便利ですね.さて,$(\clubsuit)$を確認したところ問題を解きましょう.
以下の記事も目を通しておくとよいでしょう.
<解答>
(1) $(\clubsuit)$より合成ばね定数$K$は次のように計算できます.
$\dfrac{1}{K}=\dfrac{1}{2k}+\dfrac{1}{3k}=\dfrac{5}{6k}$
$\therefore$ $K=\dfrac{6}{5}k$
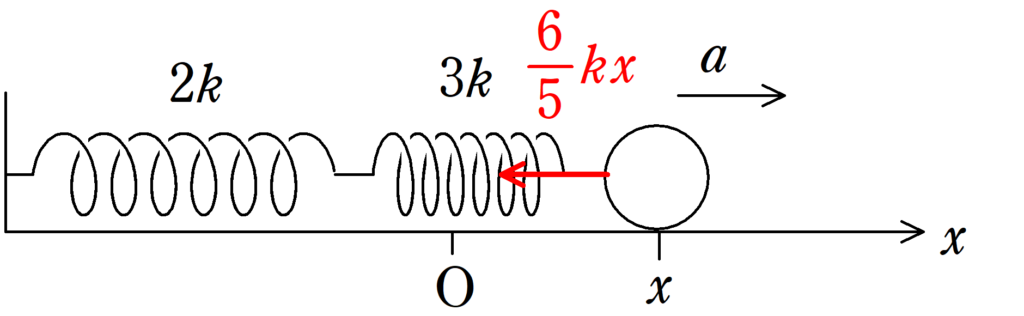
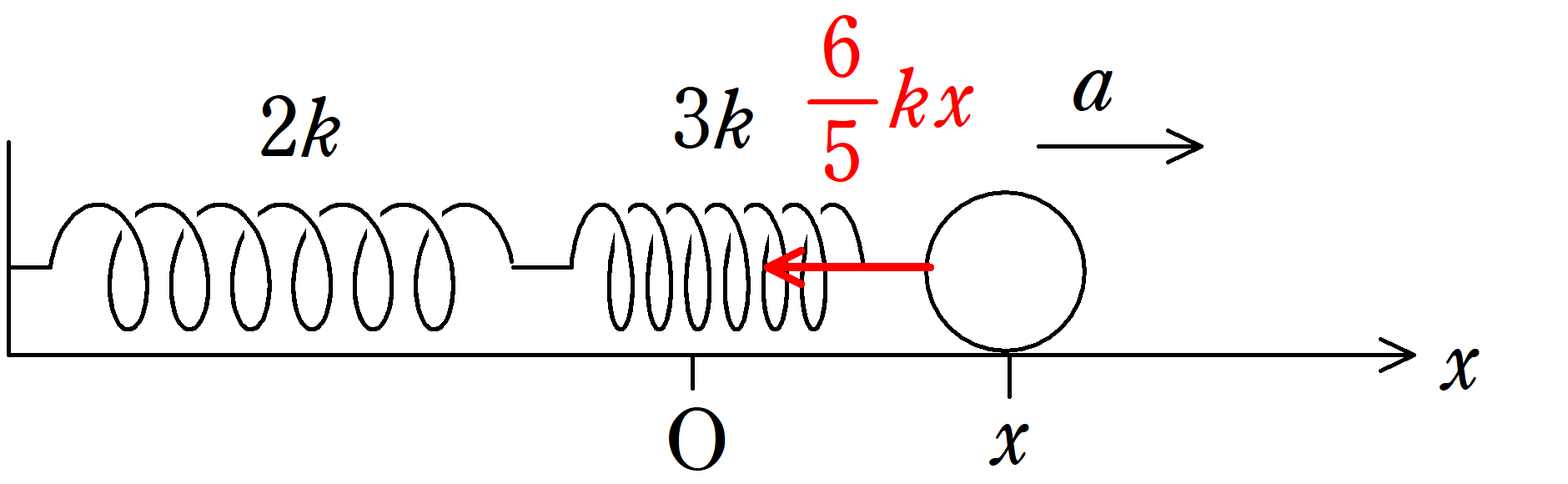
物体が位置$x$にいるときの加速度を$x$軸の正の向きに$a$とすると,運動方程式は
$ma=-\dfrac{6}{5}kx$
したがって,振動の中心は$x_{0}=0$,角振動数は$\omega=\sqrt{\dfrac{\dfrac{6}{5}k}{m}}=\sqrt{\dfrac{6k}{5m}}$,周期は$T=2\pi\sqrt{\dfrac{5m}{6k}}$となります.
(2) 振動の中心が$x_{0}=0$で$x=l$でスタートし,$x$軸の負の方向にいくので,$\cos$型です.中心と右端の距離が$l$なので,振幅は$A=l$です.したがって,時刻$t$の物体の位置$x$は
$x=A\cos \omega t=l\cos \sqrt {\dfrac{6k}{5m}}t$

問題7.1は単純に物体にはたらく力の合力を考えれば解けますが,問題7.2は直列ばねの合成を使って計算すると,物体の座標$x$を使って力をかくことができます.ちなみに,なぜ$k_{2}\Delta x_{2}$のように,片方のばねが引く力ではだめなのか理由を説明しておきましょう.
運動方程式としては間違いではないのですが,単振動の運動方程式を立てる際は,物体の座標$x$で力を表現する必要があります.そのため,片方のばねの伸びだけではなく,両方のばねの伸び縮みを入れた式が必要なのです.
また,直列合成をすると,ばね定数は小さくなります.そもそもばね定数とは
単位長さばねを伸ばすのに必要な力
なので,ばねを長くすると,単位長さ,たとえば1mばねを伸ばすのに必要な力は小さくなるんです.だから,ばね定数も小さくなります.
次回は摩擦力がはたらく場合の単振動の問題を扱います.

コメント
[…] [基本]単振動の演習問題7 運動方程式を立てる3 の続きです.今回は摩擦力がある場合の単振動です.摩擦力があってもやることは同じです.単振動の運動方程式を立て,中心座標と角振動数,周期を把握して,初期条件から振幅や位相を求めましょう. […]
[…] 単振動の演習問題⑥ 運動方程式を立てる2 の続きです. 今回は2つのばねがあるときの単振動の問題を扱います.いわゆる,ばね定数の合成を行うのですが,似ている形でも合成の仕方が全く違います.まずは,物体の両端にばねがついた問題です.… [暗記するだけでは×]波の式を立てる [基本]単振動の演習問題⑦ 運動方程式を立てる3 […]
[…] […]