
引き続き,束縛条件を立てる練習問題を扱います.
前回の内容はこちらです.
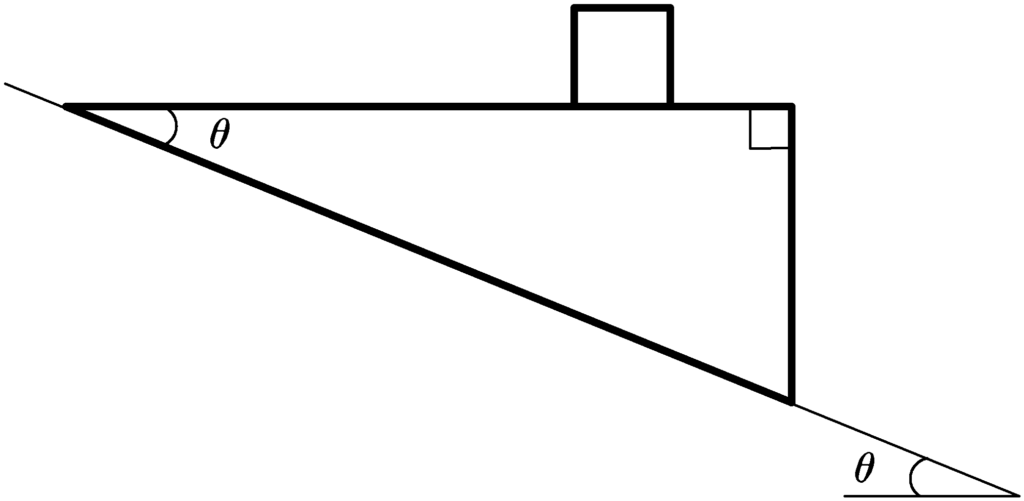
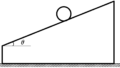
上図のように,傾角$\theta$のなめらかな斜面上に側面が$\theta$と$90^{\circ}$をもつ直角三角形の三角台を斜面上におく.さらに,三角台の上に小物体をおき,静かにはなすと,三角台,小物体ともに運動を開始した.三角台は斜面上をすべり,斜面を離れなかった.また,小物体は三角台から常に離れなかったものとする.
図の水平右向き,鉛直下向きを$x$方向,$y$方向の加速度の正の方向とすると,斜面で静止した人からみて,三角台の$x$方向の加速度は$A_{x}$,$y$方向の加速度は$A_{y}$であった.また,同じく,斜面で静止した人からみて小物体の$x$方向の加速度は$a_{x}$,$y$方向の加速度は$a_{y}$であった.このとき,次の問いに答えよ.
(1) 三角台が斜面上を離れないという,束縛条件から,$A_{x}$,$A_{y}$,$\theta$の関係を求めよ.
(2) 小物体が三角台から離れないという,束縛条件から$a_{y}$と$A_{y}$の関係を求めよ.
(1)

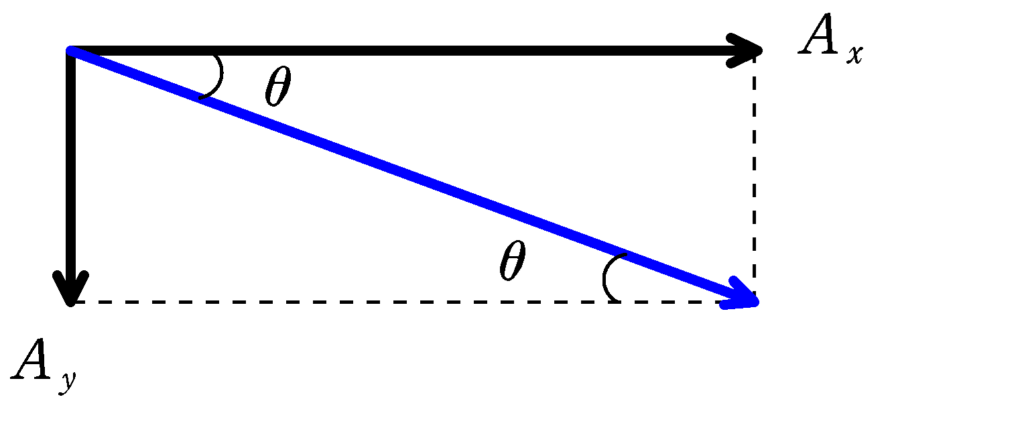
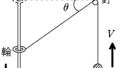
三角台は傾角$\theta$の斜面を下っているので,三角台の加速度の向きは斜面に平行な方向です.下図から,
$\dfrac{A_{y}}{A_{x}}=\tan\theta$ (答)
の関係を満たします.
(2)

前回同様に,矢印を書いて確認しましょう.
三角台からみると,鉛直方向の加速度は$0$です.そこで,三角台からみた小物体の加速度を$(★,0)$としましょう.
すると,次の関係が成り立ちます.
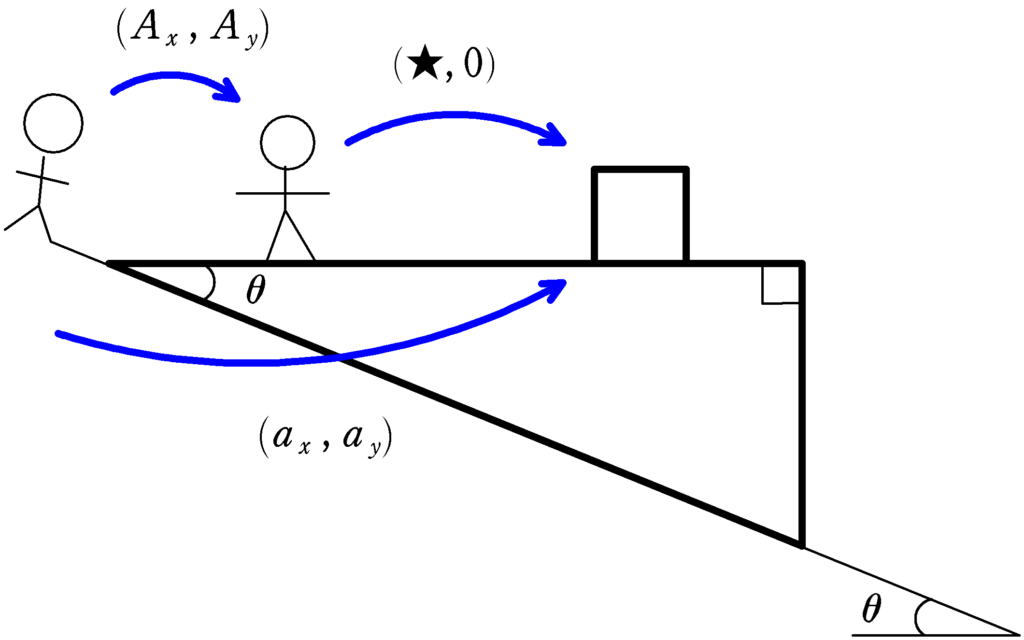
$(A_{x} , A_{y})+(★ , 0)=(a_{x} , a_{y})$
$(★ , 0)=(a_{x}-A_{x} , a_{y}-A_{y})$

したがって,
$a_{y}-A_{y}=0$
$\therefore a_{y}=A_{y}$(答)
となります.


コメント
[…] […]