
PHYさん
問題
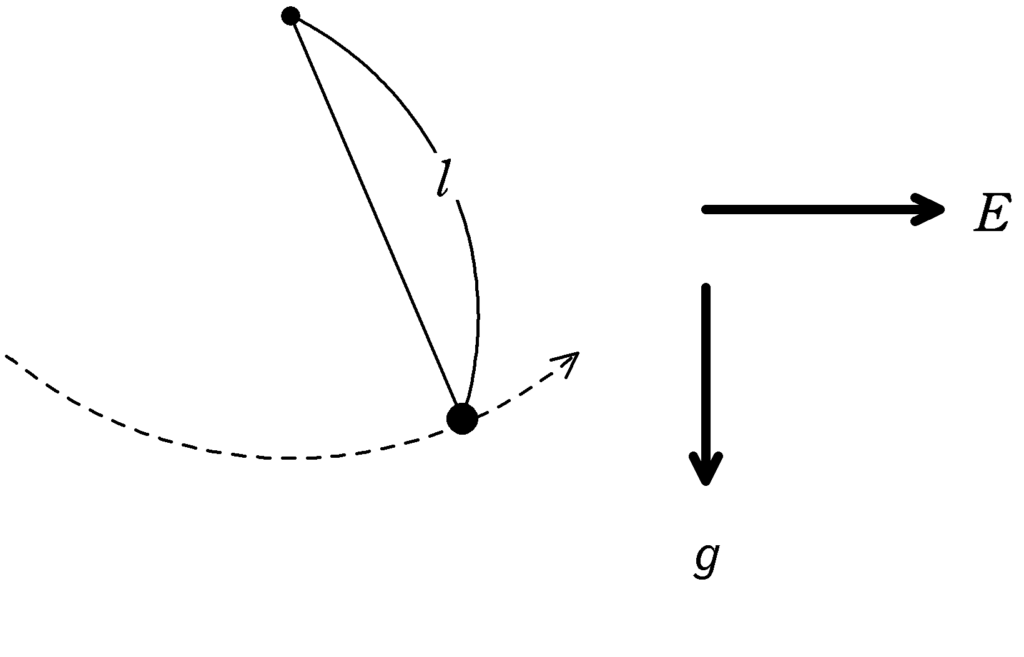
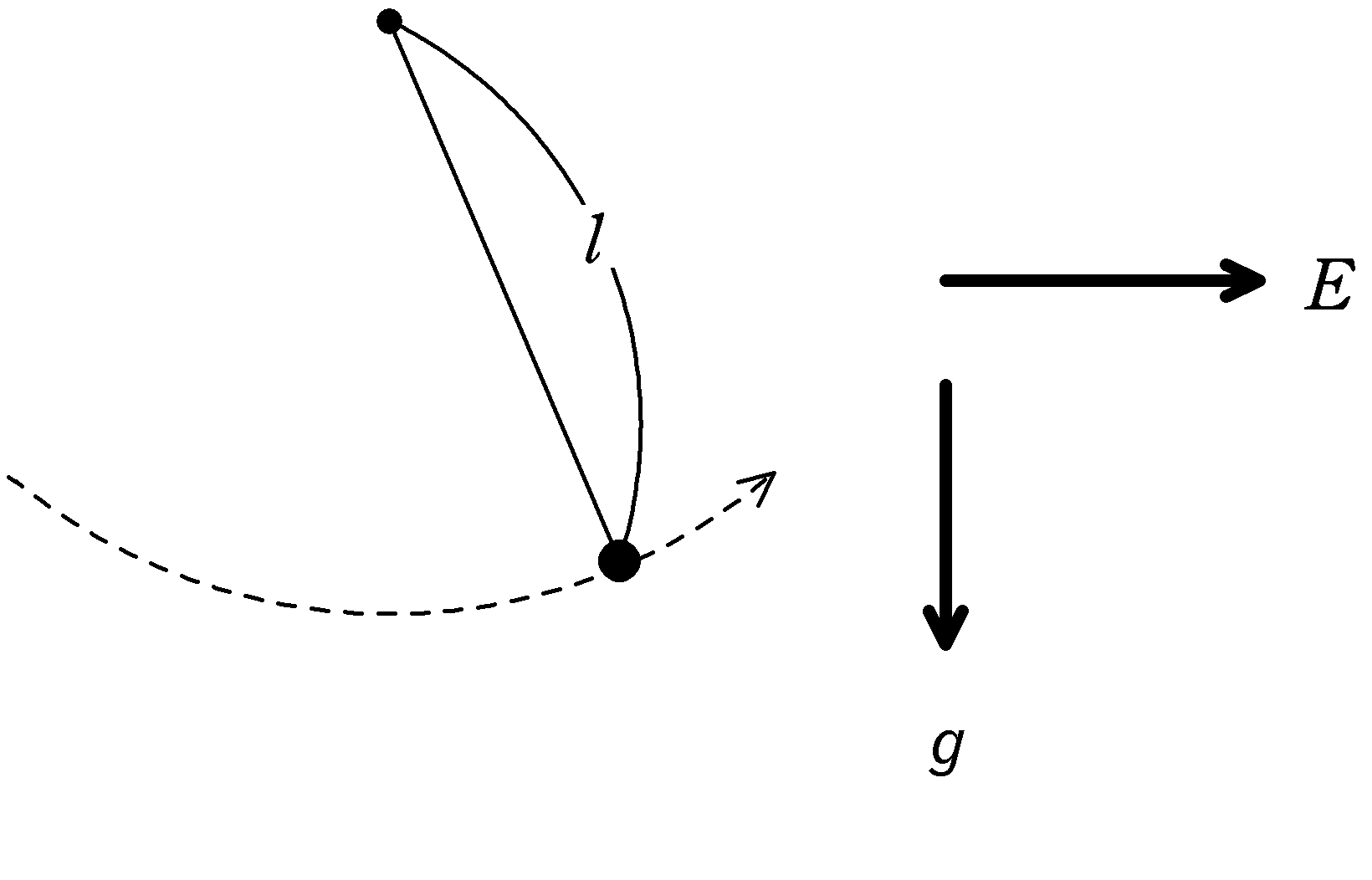
質量が$m$で電荷$q$$(>0)$の小物体を絶縁性のひもにとりつける.図のように,水平右向きに大きさ$E$の一様な電場をかけた.ひもの長さを$l$として,単振り子運動させたときの周期を求めよ.ただし,重力加速度の大きさを$g$とする.

NEKO
まずは,単振り子の周期について確認しましょう.
単振り子の周期
重力加速度の大きさが$g$,長さ$l$の質点の単振り子の周期$T$は
$T=2\pi\sqrt{\dfrac{l}{g}}$

NEKO
今回は,重力の他に静電気力がはたらくため,みかけの重力加速度を考える必要があります.
ちなみに,静電気力の大きさ$f$は,電荷$q(>0)$が電場の大きさ$E$中にあるとき
$f=qE$
となります.
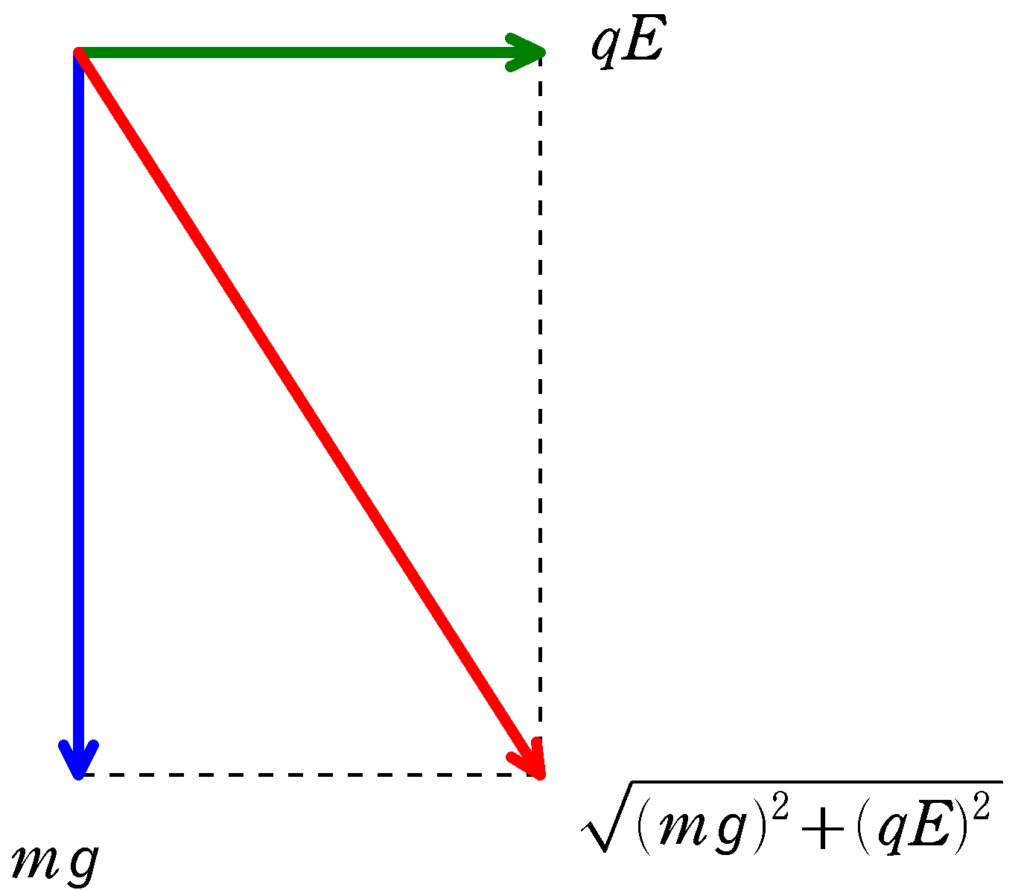
★ 重力と静電気力の合力
$F=\sqrt{(mg)^{2}+(qE)^{2}}$
みかけの重力加速度を$g^{\prime}$として
$mg^{\prime}=\sqrt{(mg)^{2}+(qE)^{2}}$
より,両辺$m$で割って
$\eqalign{g^{\prime}&=\dfrac{\sqrt{(mg)^{2}+(qE)^{2}}}{m}\\&=\sqrt{g^{2}+\left(\dfrac{qE}{m}\right)^{2}}}$

NEKO
つまり,小物体はみかけの重力加速度の大きさ$\sqrt{g^{2}+\left(\dfrac{qE}{m}\right)^{2}}$で長さ$l$の単振り子運動していると考えることができるね.
★ 周期
したがって,求める周期$T$は
$T=2\pi\sqrt{\dfrac{l}{\sqrt{g^{2}+\left(\dfrac{qE}{m}\right)^{2}}}}$ (答)

コメント