ベータトロン内部磁場を変化させると半径はどう変わるか

NEKO

前回，ベータトロンを扱ったね．

もし，円周上の磁場を「ベータトロン条件」を満たさないで変化させた場合はどんなことが起こるんだろう？

なんとなく，電子が加速するから半径が大きくなるのかな？

PHYさん

いえ，実は内部および軌道上の磁束密度を$\varPhi$から非常に短い時間$\varDelta t$の間に$\varDelta \varPhi$変化させると，半径が小さくなるように変化していきます．

NEKO

へえ，そうなるんだ．

PHYさん

では，実は内部および軌道上の磁束密度を$\varPhi$から非常に短い時間$\varDelta t$の間に$\varDelta \varPhi$変化させたときに，電子の軌道の接線方向が$v$から$v+\varDelta v$に変化したとしましょう．

ファラデーの電磁誘導の法則

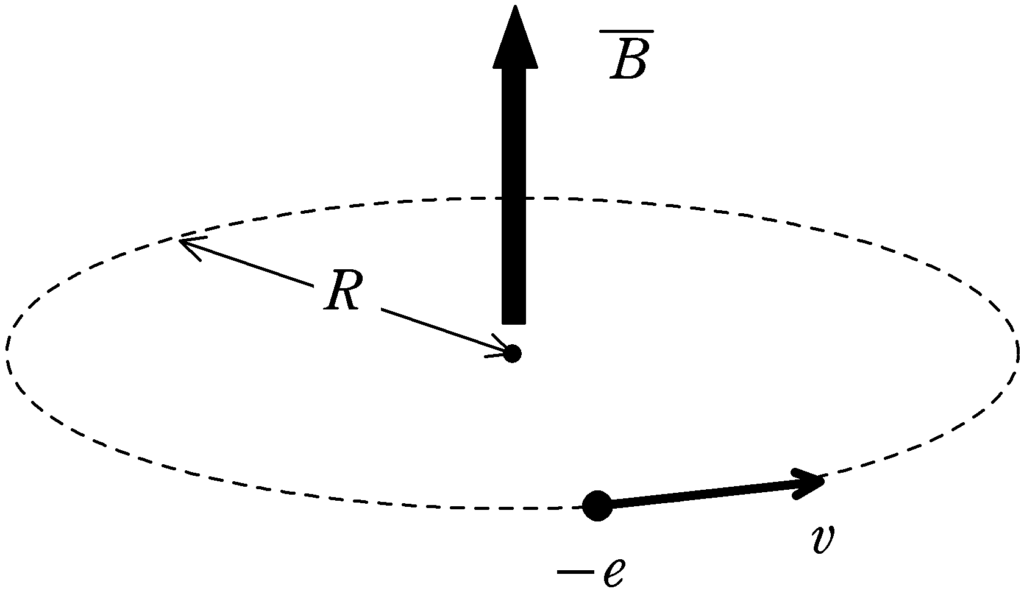
$\varDelta t$の間に磁束が$\varDelta \varPhi$変化するときに生じる誘導起電力の大きさ$V$は

$V=|\dfrac{\varDelta \varPhi}{\varDelta t}|$

$\varPhi$と$B$の関係

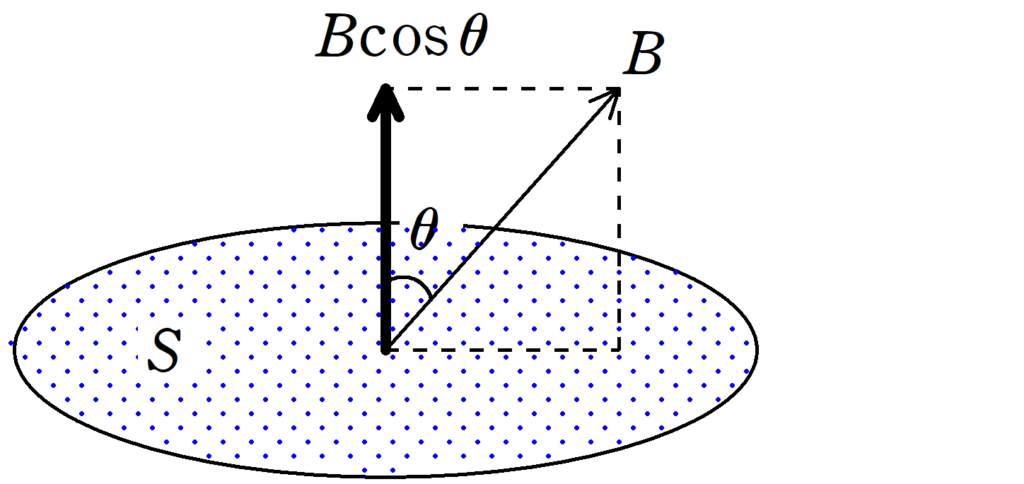
上図のように，面積$S[\rm m^{2}]$の部分を磁束密度の大きさ$B[\rm Wb/m^{2}]$の磁場が面に垂直な線に対して$\theta$の方向にかかっているとき，この面を貫く磁束$\varPhi$は

$\eqalign{\varPhi&=(B\cos\theta)S\\&=BS\cos\theta}$

となる．

★　ファラデーの法則

誘導起電力の大きさを$V$とすると

$\eqalign{V&=\dfrac{\varDelta \overline{B}\cdot \pi R^{2}}{\varDelta t}\\&=\pi R^{2}\dfrac{\varDelta \overline{B}}{\varDelta t}}$

PHYさん

次の，電場と電位差の関係より，円軌道上に生じる電場（誘導電場）の大きさを計算しましょう．

円軌道の周の長さは$2\pi R$ですね．

電場の電位差の関係

電場の大きさを$E$，距離$\Delta x$の電位差を$\Delta V$とするとき，次の関係が成り立つ．

$E=\left|\dfrac{\Delta V}{\Delta x}\right|$

★　電場と電位差の関係

周上の生じる電場の大きさを$E$として

$\eqalign{E&=\dfrac{\cancel{\pi} R^{\cancel{2}}\dfrac{\varDelta \overline{B}}{\varDelta t}}{2\cancel{\pi} \cancel{R}}\\&=\dfrac{R}{2}\dfrac{\varDelta \overline{B}}{\varDelta t}}$

PHYさん

この電場によって電子が軌道の方向に加速されます．

このときのクーロン力の大きさ$F$は，次のようになります．

★　$F$と$E$no

kankei

$F=eE=\dfrac{eR}{2}\dfrac{\varDelta \overline{B}}{\varDelta t}$

$\therefore F\varDelta t=\dfrac{eR\varDelta \overline{B}}{2}$

NEKO

電子は力積(力×時間)を受けているので，電子の運動量の大きさが変化するね．

電子の質量を$m$，速さの変化を$\varDelta v$とすると

$\eqalign{m\varDelta v&=F\varDelta t\\&=\dfrac{eR\varDelta \overline{B}}{2}}$

$\therefore \varDelta v=\dfrac{eR\varDelta \overline{B}}{2m}$ 　$\dots (\ast)$

PHYさん

加速する前は，

$m\dfrac{v^{2}}{R}=vBe$　$\dots (2\ast)$

が成り立っています．

電子の接線方向の速度が$v+\varDelta v$になったとき，電子とともに回転している観測者からみると，電子には，中心方向にローレンツ力$(v+\varDelta v)(B+\varDelta\overline{B})e$と中心方向と反対方向に遠心力$m\dfrac{(v+\varDelta v)^{2}}{R}$がはたらきます．

中心方向にはたらく力を$F$として，この力の和を計算しましょう．

次式の計算の際に$(\ast)$と$(2\ast)$を代入しています．

$\eqalign{F&=(v+\varDelta v)(B+\varDelta \overline{B})e-m\dfrac{(v+\varDelta v)^{2}}{R}\\&=\cancel{vBe}+v\left(\varDelta \overline{B}\right)e+(\varDelta v)Be+(\varDelta v)\left(\varDelta \overline{B}\right)e-\cancel{m\dfrac{v^{2}}{R}}-\dfrac{2mv(\varDelta v)}{R}-m\dfrac{(\varDelta v)^{2}}{R}\\&=v\left(\varDelta \overline{B}\right)e+\dfrac{eR\left(\varDelta \overline{B}\right)}{2m}Be+\dfrac{eR\left(\varDelta \overline{B}\right)}{2m}\cdot \left(\varDelta \overline{B}\right)e-\dfrac{\cancel{2m}v}{\cancel{R}}\cdot \dfrac{e\cancel{R}\left(\varDelta \overline{B}\right)}{\cancel{2m}}-m\dfrac{1}{R}\cdot \left\{\dfrac{eR\left(\varDelta \overline{B}\right)}{2m}\right\}^{2}\\&=v\cancel{\left(\varDelta \overline{B}\right)e}+\dfrac{e^{2}RB\left(\varDelta \overline{B}\right)}{2m}+\dfrac{e^{2}R\left(\varDelta \overline{B}\right)^{2}}{2m}-\cancel{ve(\varDelta \overline{B})}-\cancel{m}\dfrac{1}{\cancel{R}}\cdot \dfrac{e^{2}R^{\cancel{2}}\left(\varDelta \overline{B}\right)^{2}}{4m^{\cancel{2}}}\\&=\dfrac{e^{2}RB\left(\varDelta \overline{B}\right)}{2m}+\dfrac{e^{2}R\left(\varDelta \overline{B}\right)^{2}}{4m}\\&=\dfrac{e^{2}R\left(\varDelta \overline{B}\right)}{4m}\cdot (2B+\varDelta \overline{B})>0}$