
ガウスの法則の立て方はわかるんだけど,なんでこんな式が成り立つんだろう??
閉曲面$\rm C$内にある電荷の総和を$Q$とする.
電場が閉曲面に垂直に貫く面積を$S$とする.このとき,次式が成り立つ.
$ES=4\pi k_{0}|Q|$
ただし,$E$は閉曲面を垂直に貫く電場の大きさであり,$k_{0}$はクーロンの比例定数である.

では,今回はガウスの法則について説明しましょう.
閉曲面を垂直に貫く電場×面積を別表現する


電荷$Q$(ここでは$Q>0$としましょう.)を囲む閉曲面$\rm C^{\prime}$を考えます.
電荷$Q$から距離$r$の位置の電場の大きさは,クーロンの比例定数$k_{0}$を用いて
$k_{0}\dfrac{Q}{r^{2}}$
となります.
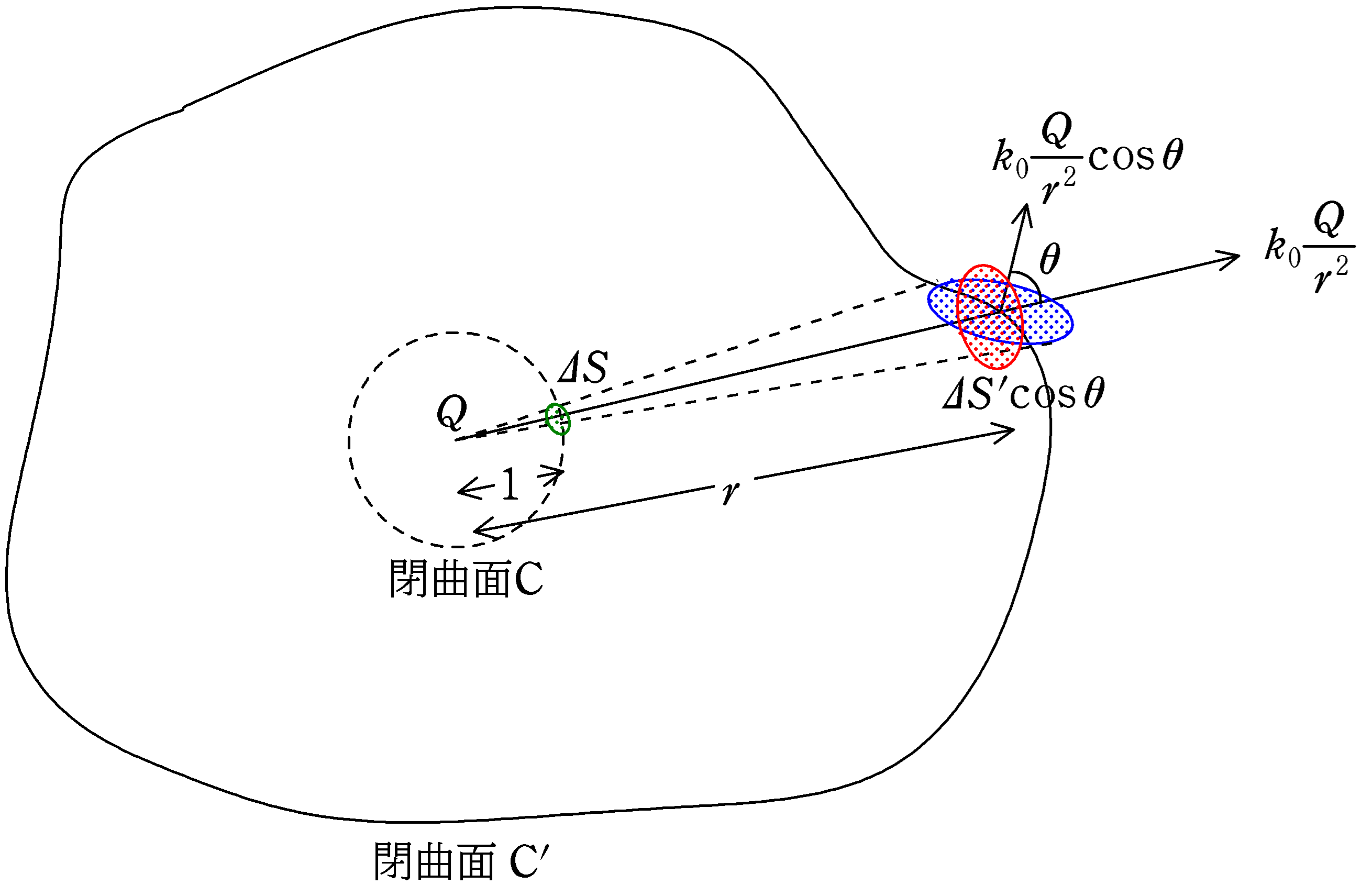
ここで,距離が$r$離れた場所に電場が貫いた付近の微小面積$\varDelta S^{\prime}$を考えましょう.
このとき,電場は貫いた面の法線からのなす角が$\theta$であるとしましょう.
すると,
微小面積$\varDelta S^{\prime}\times$ 面を垂直に貫く電場の大きさ
は,
$\varDelta S^{\prime}\times k_{0}\dfrac{Q}{r^{2}}\cos\theta$ $\dots (\ast)$
となります.

ガウスの法則は,
$\varDelta S^{\prime}\times k_{0}\dfrac{Q}{r^{2}}\cos\theta$
の式をすべての閉曲面について計算して足し合わす.と言っているんだね・・・.
でもそれって,かなり難しいんじゃないかな.そもそも閉曲面の形で変わりそうだし・・・

いえ,結論をいうと,閉曲面の形には依りません.
直接は計算できないので,次のように工夫してみたいと思います.
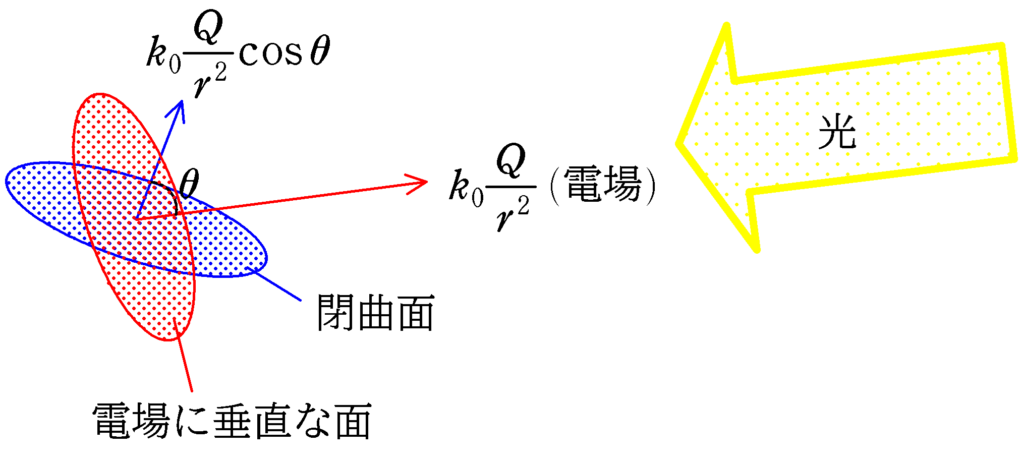

微小な閉曲面の一部(上図青色部分)に電場の方向と真逆の方向から光を当てたときの影の面積について考えてみましょう.
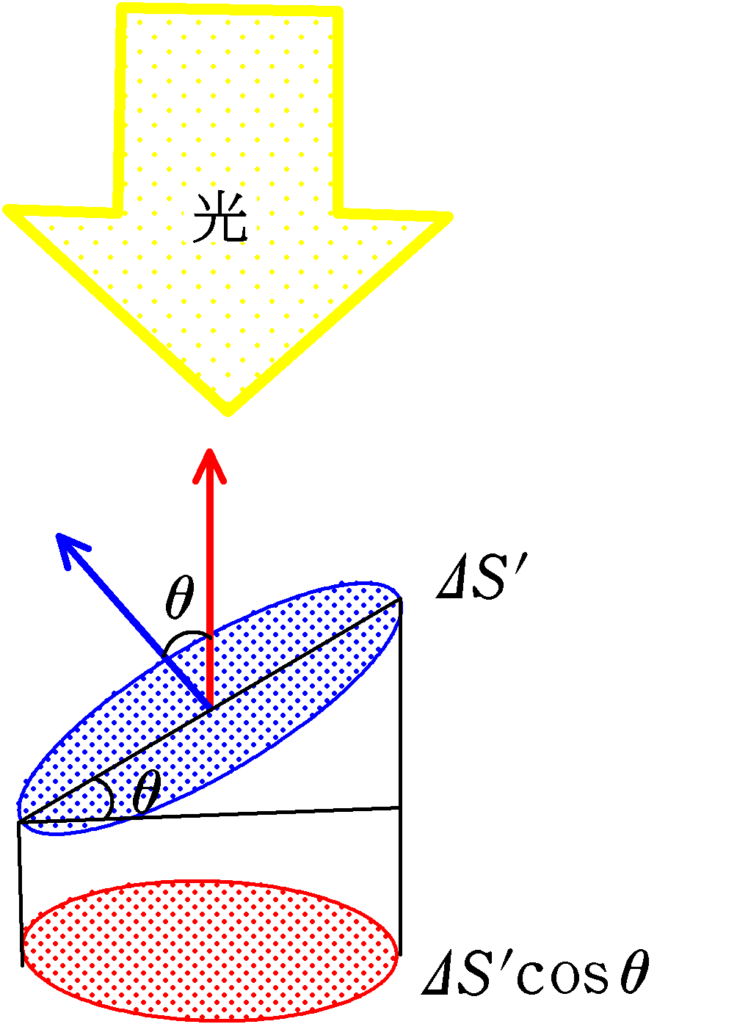

その影の面積は上図より
$\varDelta S^{\prime}\cos\theta$
となります.
すると,
電場の大きさ$\times$ 微小な閉曲面の影の面積
は,
$\varDelta S^{\prime}\cos\theta \times k_{0}\dfrac{Q}{r^{2}}$ $\dots (2\ast)$
となり,これは$(\ast)$と同じ式になります.
微小面積$\varDelta S^{\prime}\times$ 面を垂直に貫く電場の大きさ
のかわりに
電場の大きさ$\times$ 微小な閉曲面の影の面積
を計算してもよい.

これでも計算は,まだ大変そうだね・・・
半径1の球面を考えてみる.
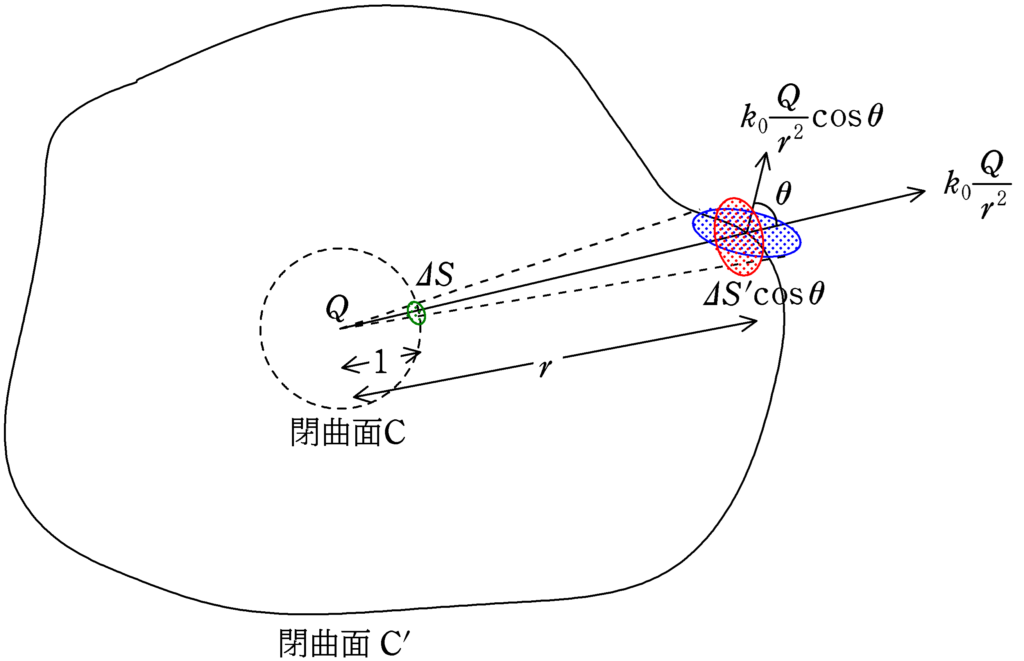

次に,電荷$Q$を中心とした,半径1の球面(閉曲面C)を考えてみましょう.
電荷$Q$がある場所を頂点として,さきほど求めた面積$\varDelta S^{\prime}\cos\theta$部分の面積を底面(上図赤色)とした錐を考えてみます.赤い部分は円でなくてもいいんですが,わかりやすいように,円錐をイメージしてもらうとよいかと思います.
この円錐と閉曲面が交わる部分が上図の緑色の部分です.
このとき,緑色部分の面積$\varDelta S$と赤色部分の面積$\varDelta S^{\prime}\cos\theta$は,相似比と面積比を考えて次のようになります.
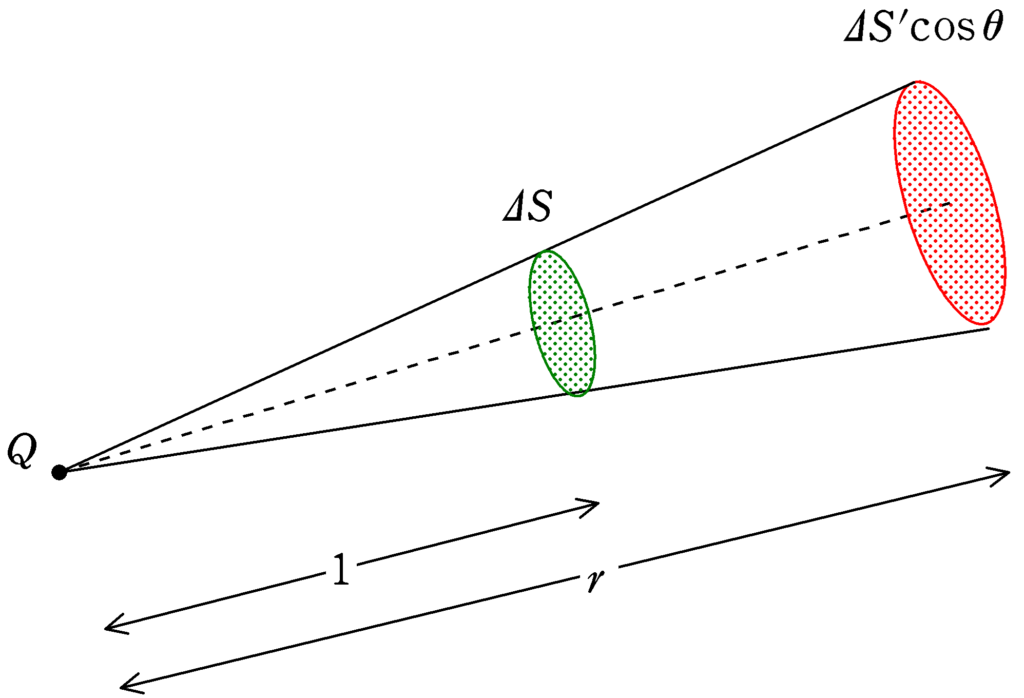
$\varDelta S:\varDelta S^{\prime}\cos\theta=1^{2}:r^{2}$
$\varDelta S^{\prime}\cos\theta=r^{2}\varDelta S$ $\dots (3\ast)$

$(3\ast)$を$\varDelta S^{\prime}\cos\theta \times k_{0}\dfrac{Q}{r^{2}}$ $(2\ast)$に代入すると次のようになります.
$\eqalign{\varDelta S^{\prime}\cos\theta \times k_{0}\dfrac{Q}{r^{2}}&=\cancel{r^{2}}\varDelta Sk_{0}\dfrac{Q}{\cancel{r^{2}}}&=k_{0}Q\varDelta S}$

つまり,
電場の大きさ$\times$ 微小な閉曲面の影の面積
の代わりに
閉曲面$\rm C$の面積$\times k_{0}Q$
を考えてもいいだね.
これなら,計算は簡単そう.
微小面積$\varDelta S^{\prime}\times$ 面を垂直に貫く電場の大きさ
のかわりに
電場の大きさ$\times$ 微小な閉曲面の影の面積
を計算してもよい.また,この代わりに
閉曲面$\rm C$の面積$\times k_{0}Q$
を計算してもよい.
全部足し合わせる
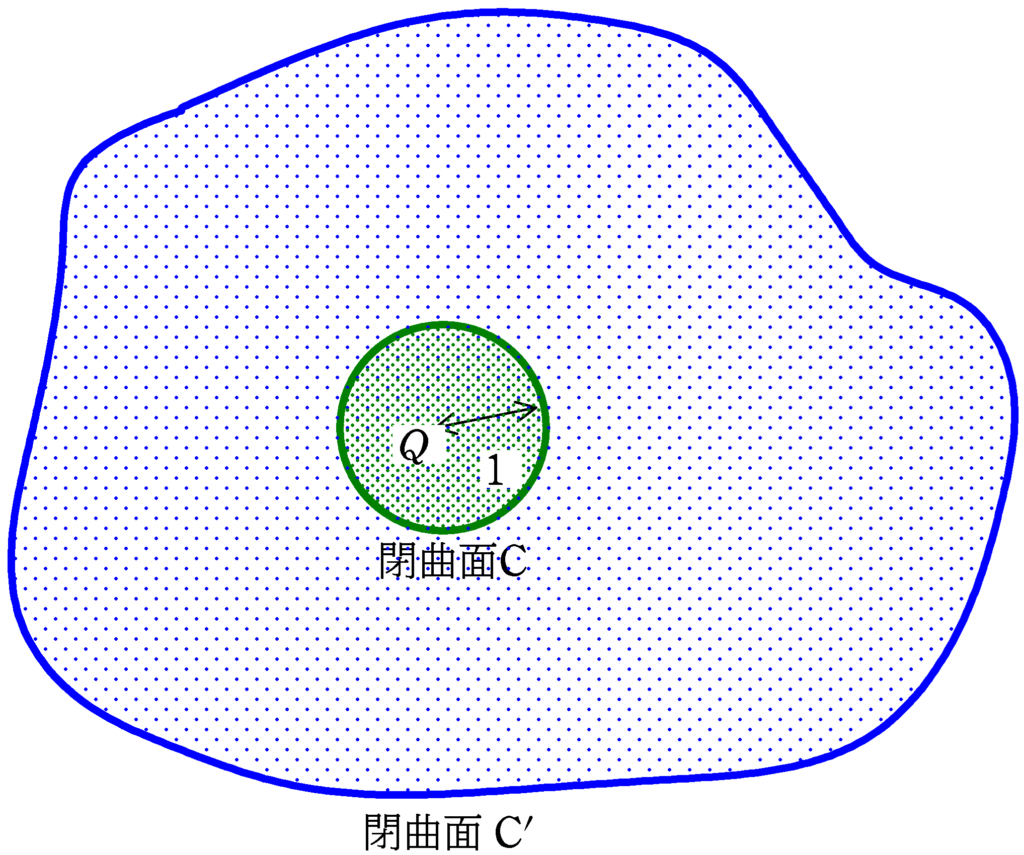

つまり,
閉曲面$\rm C^{\prime}$を垂直に貫く電場の大きさ$\times$面積の和
は,
閉曲面$\rm C$の面積の和$\times k_{0}Q$
を計算すればいいんだね.閉曲面$\rm C$の面積は$4\pi 1^{2}$だから
$4\pi k_{0}Q$
となるね.

はい,このように,閉曲面はどのようにとっても結局$4\pi k_{0}Q$となります.
これは,電荷が2個あっても3個あっても同様に考えることができるので,閉曲面を$\rm C^{\prime}$をうまく選べば,多数電荷が集まった場合の電場の大きさの計算ができるというわけです.
電荷が閉曲面の外にある場合はどうするか?

電場が閉曲面から出る方向を$+$,入り込む方向を$-$とすると,次の図から,閉曲面の外にある電荷は
閉曲面に垂直な電場(符号付き)$\times $閉曲面を貫く面積は0
になることがわかります.
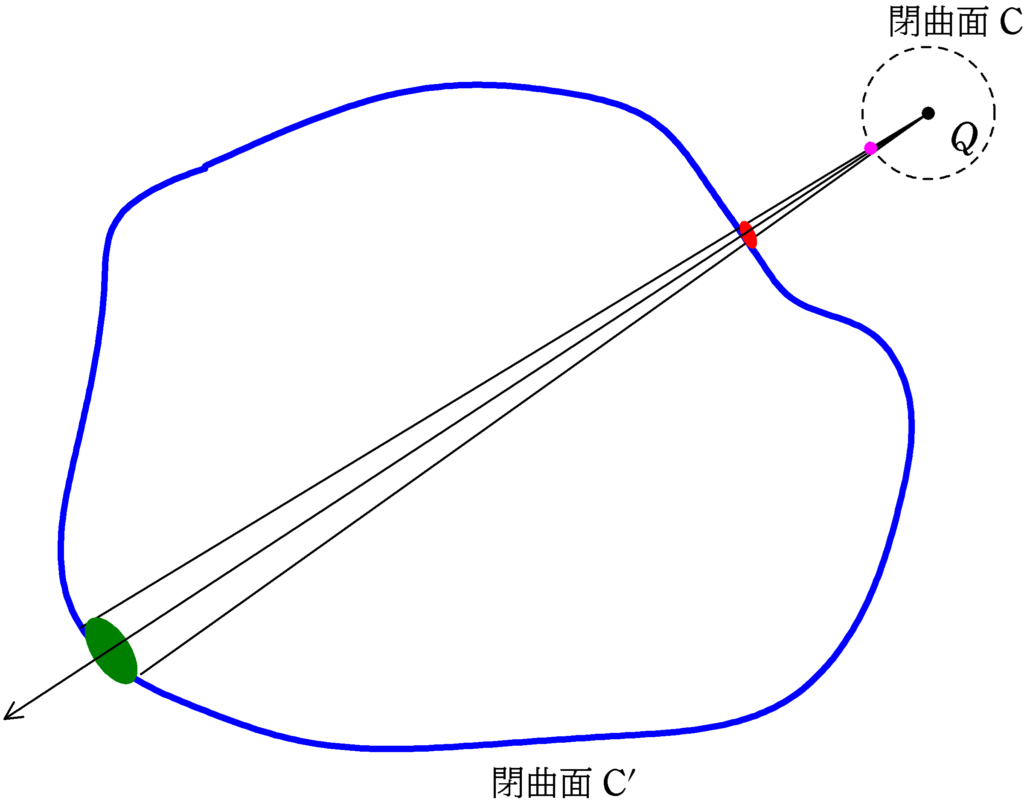
★ 赤い部分の閉曲面に垂直な電場(符号付き)$\times $閉曲面を貫く面積
閉曲面$\rm C^{\prime}$に入り込んでいるので符号はマイナス.今まで考えてきたように,赤の部分については,ピンク色の(半径1の閉曲面$\rm C$)の面積$\varDelta S$を用いて
$-k_{0}Q\varDelta S$
となる.
★ 緑部分の閉曲面に垂直な電場(符号付き)$\times $閉曲面を貫く面積
閉曲面$\rm C^{\prime}$にから出ているので符号はプラス.今まで考えてきたように,緑の部分については,ピンク色の(半径1の閉曲面$\rm C$)の面積$\varDelta S$を用いて
$k_{0}Q\varDelta S$

結局,閉曲面の外に電荷があると電気力線が入って出ていくから和が0になるんだね!

最後に,ガウスをまとめるとガウスの法則は次のようになります.
まとめ
閉曲面を垂直に貫く電場を$E_{\perp}$(閉曲面を出ていくとき「+」,入るとき,「-」と約束します.),電場が貫く面積を$\varDelta S$,閉曲面内にある電荷の総和を$\sum{Q}$,クーロンの比例定数を$k_{0}$,誘電率を$\varepsilon_{0}$とすると
$E_{\perp}\cdot \varDelta S$の和$=4\pi k_{0}\sum{Q}=\dfrac{\sum{Q}}{\varepsilon_{0}}$


コメント