
前回の内容はこちらです.

引き続き問題を解いていきましょう.
まずは,相互インダクタンスを求める手順の確認です.
ソレノイドコイル1が電流を流し,ソレノイドコイル2に生じる誘導起電力を考える.
コイル2の巻き数を$N_{2}$とする.コイル2に生じる誘導起電力の大きさ$V_{2}$は,時間$\varDelta t$の間にコイル2内部の磁束が$\varDelta \varPhi_{2}$変化したとき
$V_{2}=N_{2}|\frac{\varDelta \varPhi_{2}}{\varDelta t}|$ $\dots (\sharp)$
である.$\varPhi_{2}$はコイル1によって作られた磁束密度を$B_{1}$,コイル2の断面積を$S_{2}$とする.(ちなみに,コイル1とコイル2の軸は平行であるとする.)このとき,
$\varPhi_{2}=B_{1}S_{2}$ $\dots (2\sharp)$
透磁率を$\mu$,コイル1がつくる磁場を$H_{1}$とすると
$B_{1}=\mu H_{1}$ $\dots (3\sharp)$
であり,コイル1の長さを$l_{1}$,巻き数を$N_{1}$(単位長さ当たりの巻き数を$n_{1}=\dfrac{N_{1}}{l_{1}}$)とすると,ソレノイドコイル1に電流$i_{1}$を流したときにコイル内部に生じる磁場$H_{1}$は
$H_{1}=\dfrac{N_{1}}{l_{1}}i_{1}=n_{1}i_{1}$ $\dots (4\sharp)$
$(2\sharp)$から$(4\sharp)$を$(\sharp)$に代入する
$(4\sharp)$を$(3\sharp)$に代入して(以後,$n_{1}$を採用して計算する.)
$B_{1}=\mu\cdot n_{1}i_{1}$
これを$(2\sharp)$に代入して
$\varPhi_{2}=\mu n_{1}S_{2}i_{1}$
さらにこれを$(\sharp)$に代入して
$\eqalign{V_{2}&=N_{2}\left|\dfrac{\varDelta ( \mu n_{1}S_{2}i_{1} )}{\varDelta t}\right|\\&=\mu n_{1}N_{2}S_{2}\left|\dfrac{\varDelta i_{1}}{\varDelta t}\right|}$
上式の$\left|\dfrac{\varDelta i_{1}}{\varDelta t}\right|$の正の比例定数が相互インダクタンスである.(ここでは,$ \mu n_{1}N_{2}S_{2} $)
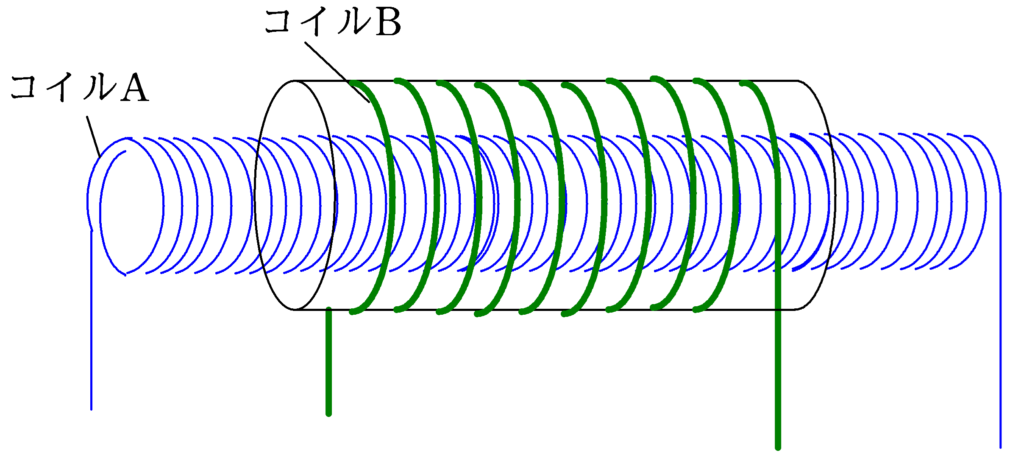
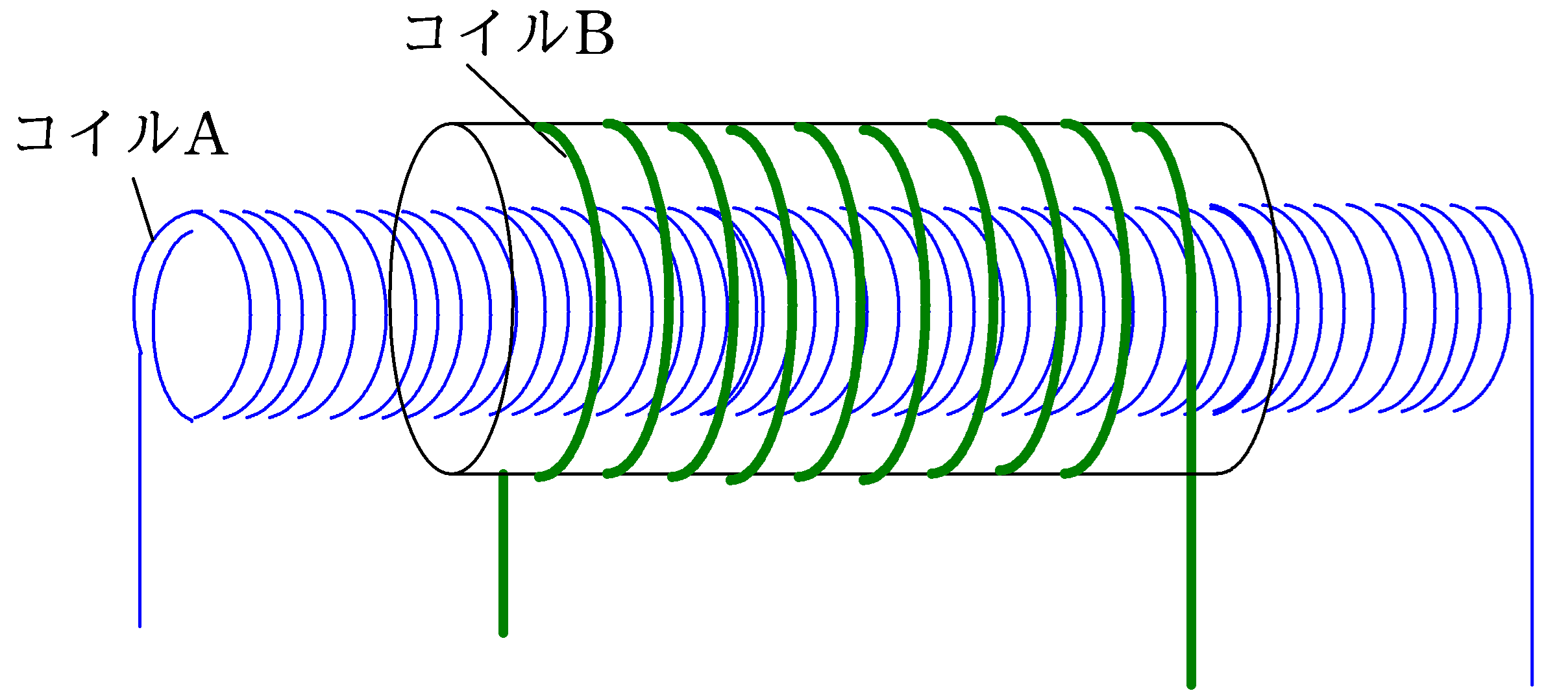
(1) ソレノイドコイルAは断面積$S_{\rm A}$で,長さが$l_{\rm A}$,総巻き数が$N_{\rm A}$であり,ソレノイドコイルBは 断面積$S_{\rm B}$で,長さが$l_{\rm B}$,総巻き数が$N_{\rm B}$である.$S_{\rm A}<S_{\rm B}$かつ$l_{\rm A}>l_{\rm B}$であり,$l_{\rm A}$は十分大きく,ソレノイドコイルAに電流を流すとコイルA内部には一様な磁場ができる.透磁率を$\mu$として,コイルAとコイルBの相互インダクタンスを$M$を求めよ.
(2) ソレノイドコイルAは断面積$S_{\rm A}$で,長さが$l_{\rm A}$,総巻き数が$N_{\rm A}$であり,ソレノイドコイルBは 断面積$S_{\rm B}$で,長さが$l_{\rm B}$,単位長さあたりの巻き数が$n_{\rm B}$である.$S_{\rm A}<S_{\rm B}$かつ$l_{\rm A}>l_{\rm B}$であり,$l_{\rm A}$は十分大きく,ソレノイドコイルAに電流を流すとコイルA内部には一様な磁場ができる.透磁率を$\mu$として,コイルAとコイルBの相互インダクタンスを$M$を求めよ.
(3) ソレノイドコイルAは断面積$S_{\rm A}$で,長さが$l_{\rm A}$,単位長さ当たりの巻き数が$n_{\rm A}$であり,ソレノイドコイルBは 断面積$S_{\rm B}$で,長さが$l_{\rm B}$,単位長さあたりの巻き数が$n_{\rm B}$である.$S_{\rm A}<S_{\rm B}$かつ$l_{\rm A}>l_{\rm B}$であり,$l_{\rm A}$は十分大きく,ソレノイドコイルAに電流を流すとコイルA内部には一様な磁場ができる.透磁率を$\mu$として,コイルAとコイルBの相互インダクタンスを$M$を求めよ.

今回も「総巻き数」なのか「単位長さあたりの巻き数」なのかに注意しましょう.
総巻き数を$N$,長さを$l$,単位長さあたりの巻き数を$n$とすると
$n=\dfrac{N}{l}$
の関係があります.
ファラデーの法則の
$V=N|\dfrac{\varDelta \varPhi}{\varDelta t}|$
の$N$は総巻き数で,ソレノイドコイルに電流$i$を流したときに内部に生じる磁場$H$の
$H=ni$
の$n$は単位長さあたりの巻き数です.
この2つの違いに注意して問題を解きましょう.
また,相互インダクタンスを求める際はいずれもコイルAに電流を流したときのことを考えましょう.
<解答>
(1)
コイルAに電流$i_{\rm A}$を流すとコイルA内の磁場$H_{\rm A}$は
$H_{\rm A}=\dfrac{N_{\rm A}}{l_{\rm A}}i_{\rm A}$
したがって,磁束密度$B_{\rm A}$は
$\eqalign{B_{\rm A}&=\mu H_{\rm A}\\ &=\mu \cdot \dfrac{N_{\rm A}}{l_{\rm A}}i_{\rm A}}$
さらに,コイルBを貫く磁束$\varPhi_{\rm B}$は
$\eqalign{\varPhi_{\rm B}&=B_{\rm A}\cdot S_{\rm A}\\ &= \mu \cdot \dfrac{N_{\rm A}S_{\rm A}}{l_{\rm A}}i_{\rm A} }$
したがって,$\dfrac{\varDelta i_{\rm A}}{\varDelta t}>0$のとき,コイル2に生じる誘導起電力の大きさ$V$は
$\eqalign{V&=N_{\rm B}\dfrac{\varDelta \varPhi_{B}}{\varDelta t}\\&=N_{\rm B}\cdot \dfrac{\varDelta }{\varDelta t}\left(\mu \cdot \dfrac{N_{\rm A}S_{\rm A}}{l_{\rm A}}i_{\rm A}\right) \\&=\mu \dfrac{N_{\rm A}N_{\rm B}S_{\rm A}}{l_{\rm A}}\dfrac{\varDelta i_{\rm A}}{\varDelta t}}$
したがって,相互インダクタンスは
$M= \mu \dfrac{N_{\rm A}N_{\rm B}S_{\rm A}}{l_{\rm A}} $ (答)
(2)
コイルAに電流$i_{\rm A}$を流すとコイルA内の磁場$H_{\rm A}$は
$H_{\rm A}=\dfrac{N_{\rm A}}{l_{\rm A}}i_{\rm A}$
したがって,磁束密度$B_{\rm A}$は
$\eqalign{B_{\rm A}&=\mu H_{\rm A}\\ &=\mu \cdot \dfrac{N_{\rm A}}{l_{\rm A}}i_{\rm A}}$
さらに,コイルBを貫く磁束$\varPhi_{\rm B}$は
$\eqalign{\varPhi_{\rm B}&=B_{\rm A}\cdot S_{\rm A}\\ &= \mu \cdot \dfrac{N_{\rm A}S_{\rm A}}{l_{\rm A}}i_{\rm A} }$
コイルの総巻き数は$n_{\rm B}l_{\rm B}$である.したがって,$\dfrac{\varDelta i_{\rm A}}{\varDelta t}>0$のとき,コイル2に生じる誘導起電力の大きさ$V$は
$\eqalign{V&= n_{\rm B}l_{\rm B} \dfrac{\varDelta \varPhi_{B}}{\varDelta t}\\&= n_{\rm B}l_{\rm B} \cdot \dfrac{\varDelta }{\varDelta t}\left(\mu \cdot \dfrac{N_{\rm A}S_{\rm A}}{l_{\rm A}}i_{\rm A}\right) \\&=\mu \dfrac{N_{\rm A} n_{\rm B}l_{\rm B} S_{\rm A}}{l_{\rm A}}\dfrac{\varDelta i_{\rm A}}{\varDelta t}}$
したがって,相互インダクタンスは
$M= \mu \dfrac{N_{\rm A} n_{\rm B}l_{\rm B} S_{\rm A}}{l_{\rm A}} $ (答)
(3)
コイルAに電流$i_{\rm A}$を流すとコイルA内の磁場$H_{\rm A}$は
$H_{\rm A}=n_{\rm A}i_{\rm A}$
したがって,磁束密度$B_{\rm A}$は
$\eqalign{B_{\rm A}&=\mu H_{\rm A}\\ &=\mu \cdot n_{\rm A}i_{\rm A}}$
さらに,コイルBを貫く磁束$\varPhi_{\rm B}$は
$\eqalign{\varPhi_{\rm B}&=B_{\rm A}\cdot S_{\rm A}\\ &= \mu \cdot n_{\rm A}S_{\rm A}i_{\rm A} }$
コイルの総巻き数は$n_{\rm B}l_{\rm B}$である.したがって,$\dfrac{\varDelta i_{\rm A}}{\varDelta t}>0$のとき,コイル2に生じる誘導起電力の大きさ$V$は
$\eqalign{V&= n_{\rm B}l_{\rm B} \dfrac{\varDelta \varPhi_{B}}{\varDelta t}\\&= n_{\rm B}l_{\rm B} \cdot \dfrac{\varDelta }{\varDelta t}\left(\mu \cdot n_{\rm A}S_{\rm A}i_{\rm A}\right) \\&=\mu n_{\rm A} n_{\rm B}l_{\rm B}S_{\rm A}\dfrac{\varDelta i_{\rm A}}{\varDelta t}}$
したがって,相互インダクタンスは
$M= \mu n_{\rm A} n_{\rm B}l_{\rm B}S_{\rm A} $ (答)

コメント