
今回は摩擦力がある場合の単振動です.摩擦力があってもやることは同じです.単振動の運動方程式を立て,中心座標と角振動数,周期を把握して,初期条件から振幅や位相を求めましょう.
前回の内容はこちら
それでは,さっそく問題を解きましょう.
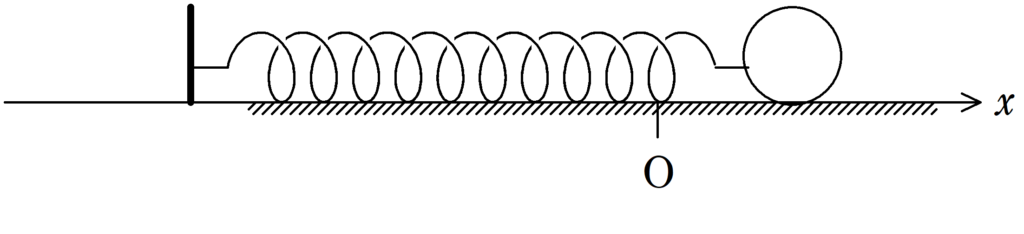
上図のように,水平な床の上に質量$m$の物体がおいてある.ばね定数$k$のばねの一端は床に固定された板にとりつけられ,他端は物体にとりつけた.自然長になるときの物体の位置を原点として,ばねが伸びる方向に$x$軸をとる.物体の位置が$x=L(L>0)$になるところまでばねを伸ばして静かに手をはなすと物体は単振動をした.物体が動き出した時刻を$t=0$とし,物体が動き出してからはじめて静止する時刻を$t=\tau$とする.ただし,ばねは軽く,物体と床とのあいだの動摩擦係数を$\mu$とする.また,重力加速度の大きさを$g$とする.このとき,次の問いに答えよ.
(1) $0 \leqq t\leqq \tau$の間の運動について,振動の中心座標$x_{0}$,角振動数$\omega$,周期$T$を$k$,$m$,$\mu$,$g$から必要なものを用いて表せ.
(2) $0 \leqq t\leqq \tau$の間の運動について,時刻$t$における物体の座標$x$を$k$,$m$,$\mu$,$g$,$t$から必要なものを用いて表せ.
(3) $\tau$を$k$,$m$,$\mu$,$g$から必要なものを用いて表せ.
<解答>
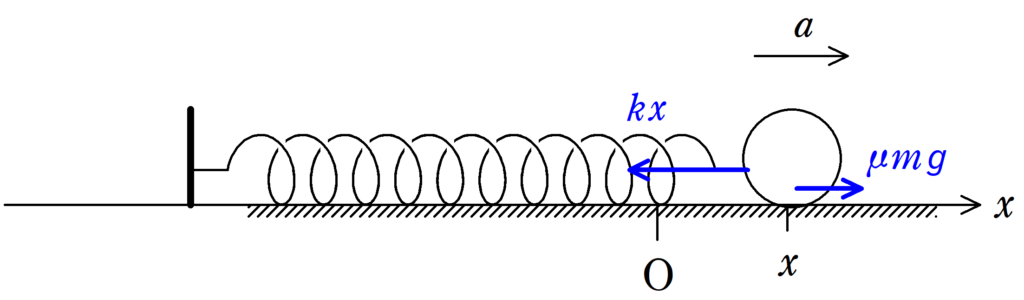
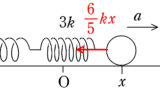
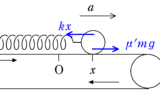
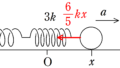
(1) 運動方程式を立てます.物体は$x=L$を出発してから$x$軸の負の方向に速度をもっているので,動摩擦力がはたらく向きは$x$軸の正方向です.位置$x$における加速度を$x$軸の正の向きに$a$と設定しましょう.加速度の向きは座標の向きと一致させておいたほうがよいです.運動方程式は
$ma=-kx+\mu mg=-k\left(x-\dfrac{\mu mg}{k}\right)$
なので,中心座標は$x_{0}=\dfrac{\mu mg}{k}$,角振動数は$\omega=\sqrt{\dfrac{k}{m}}$,周期は$T=2\pi\sqrt{\dfrac{m}{k}}$となります.
(2) 振幅に注意しましょう.

振幅は振動の端から中心までの距離です.今回は振動のスタートは$x=L$です.(静かにはなした→速度0ではなした→振動の端)さらに(1)で調べた通り,振動の中心は$x_{0}=\dfrac{\mu mg}{k}$なので,中心から右端までの距離は$L-\dfrac{\mu mg}{k}$となります.また,最大の位置から$x$軸の負の方向へスタートしているので$\cos$型です.したがって,時刻$t$における座標$x$は
$x=\dfrac{\mu mg}{k}+\left(L-\dfrac{\mu mg}{k}\right)\cos \sqrt{\dfrac{k}{m}}t$ $\cdots (\ast)$
(3) 振動の左端の位置は振幅$A$を使って$x_{0}-A$です.$A=L-\dfrac{\mu mg}{k}$なので,左端の位置$x_{\rm{L}}$は
$x_{\rm{L}}=\dfrac{2\mu mg}{k}-L$
となります.($\ast$)は座標$x$と時刻$t$の関係式なので,時刻を指定すると座標がわかりますし,座標を代入すると時刻を推定できます.そこで,$x_{\rm{L}}$を($\ast$)に代入してみましょう.
$\dfrac{2\mu mg}{k}-L=\dfrac{\mu mg}{k}+\left(L-\dfrac{\mu mg}{k}\right)\cos \sqrt{\dfrac{k}{m}}t$
$-\left(L-\dfrac{\mu mg}{k}\right)=\left(L-\dfrac{\mu mg}{k}\right)\cos \sqrt{\dfrac{k}{m}}t$
$\cos \sqrt{\dfrac{k}{m}}t=-1$
このような解は無数にありますが,一番小さい正の数$t$が$\tau$です.
$\sqrt{\dfrac{k}{m}}\tau=\pi$ $\therefore$ $\tau=\pi\sqrt{\dfrac{m}{k}}$
つまり,周期$T$の半分ですね.このくらいの問題であれば,わざわざこのような大変な計算をしなくてもよいですが,確認のため計算してみました.

さて,もう1題です.
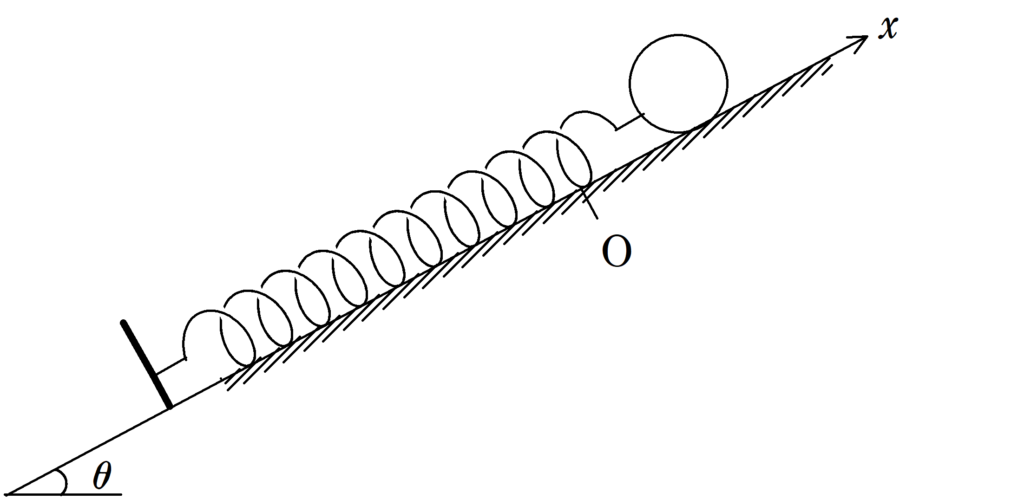
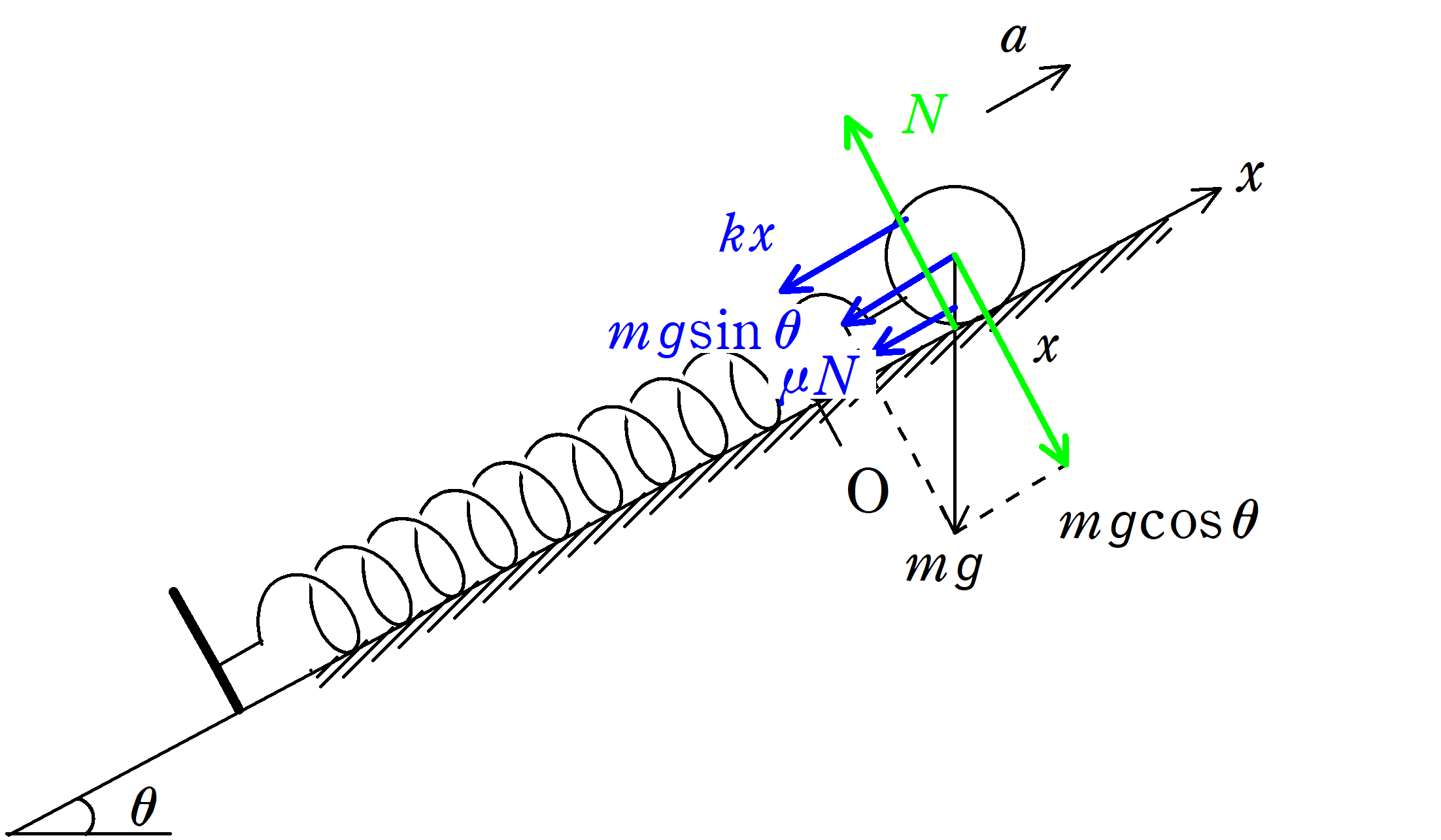
上図のように,傾角$\theta$の斜面に質量$m$の物体がおいてある.ばね定数$k$のばねの一端は斜面に固定された板にとりつけられ,他端は物体にとりつけた.自然長になるときの物体の位置を原点として,ばねが伸びる方向に$x$軸をとる.物体の位置が$x=-L(L>0)$になるところまでばねを縮ませて静かに手をはなすと物体は自然長に戻る方向に動き出し単振動をした.物体が動き出した時刻を$t=0$とし,物体が動き出してからはじめて静止する時刻を$t=\tau$とする.ただし,ばねは軽く,物体と斜面とのあいだの動摩擦係数を$\mu$とする.また,重力加速度の大きさを$g$とする.このとき,次の問いに答えよ.
(1) $0 \leqq t\leqq \tau$の間の運動について,振動の中心座標$x_{0}$,角振動数$\omega$,周期$T$を$k$,$m$,$\mu$,$g$,$\theta$から必要なものを用いて表せ.
(2) $0 \leqq t\leqq \tau$の間の運動について,時刻$t$における物体の座標$x$を$k$,$m$,$\mu$,$g$,$\theta$,$t$から必要なものを用いて表せ.
<解答>
(1) 問題7.1と違うのは斜面になったというだけではありません.$0 \leqq t\leqq \tau$の間は$x$軸の正方向に速度をもっているので,動摩擦力がはたらく向きは$x$軸の負の向きとなることに注意しましょう.また,動摩擦力の大きさは(動摩擦係数)×(垂直抗力)です.垂直抗力は$mg$ではありません.真面目に,斜面に垂直な方向のつり合いの式を立てて確認しましょう.
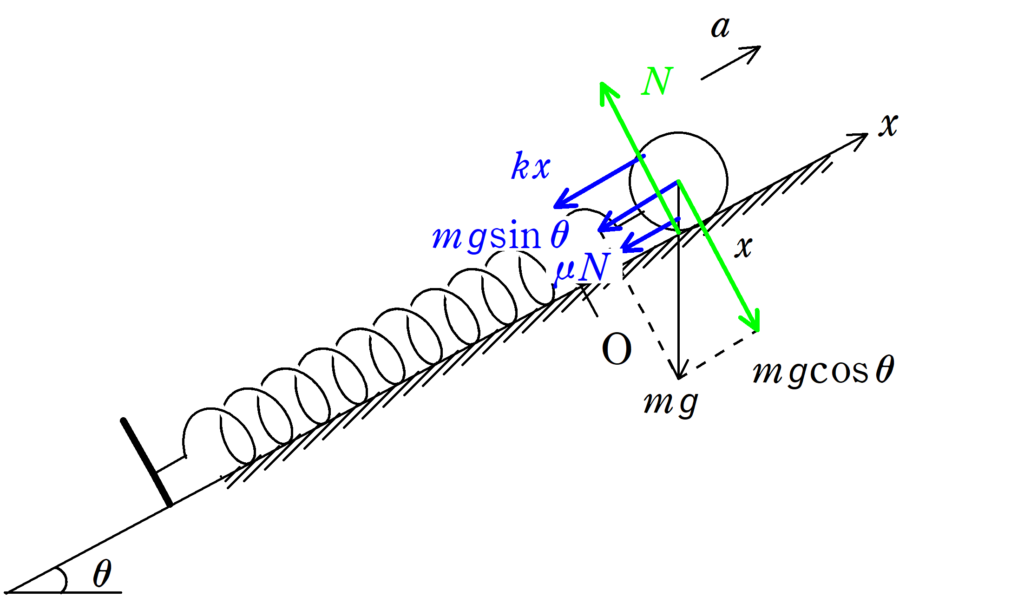
位置$x$(今回も$x>0$で考えました.動き出した瞬間は負の位置にいますが,しばらくすると物体は原点を超えて正の位置にいくはずです.$x<0$で考える場合は向きと大きさに注意です)における力を図示すると上のようになります.加速度は$x$軸の正方向にとって,運動方程式は
$ma=-kx-mg\sin \theta -\mu N$ $\cdots (\ast)$
また,垂直抗力の大きさを$N$として,斜面垂直な方向のつり合いの式は
$N=mg\cos \theta$ $\cdots (2\ast)$
($2\ast$)を($\ast$)に代入して$N$を消去すると
$\eqalign{ma&=-kx-mg\sin \theta -\mu mg\cos \theta\\&=-k\left(x+\dfrac{\sin \theta +\mu\cos \theta}{k}mg\right)}$
この運動方程式より,中心座標は$x_{0}=-\dfrac{\sin \theta +\mu \cos \theta}{k}mg$,角振動数は$\omega=\sqrt{\dfrac{k}{m}}$,周期は$T=2\pi\sqrt{\dfrac{m}{k}}$となります.
(2) 中心が$x_{0}=-\dfrac{\sin \theta +\mu \cos \theta}{k}mg$,左端が$x=-L$なので振幅$A$は
$A=x_{0}-(-L)=-\dfrac{\sin \theta +\mu \cos \theta}{k}mg+L$
となります.また,最小の位置から$x$軸の正方向へスタートするので$-\cos$型です.したがって,時刻$t$における物体の位置$x$は
$x=-\dfrac{\sin \theta +\mu \cos \theta}{k}mg-\left(L-\dfrac{\sin \theta +\mu \cos \theta}{k}mg\right)\cos\sqrt{\dfrac{k}{m}}t$
となります.

かなり,複雑な答えになりましたね.複雑な問題になっても,何をすればよいのか忘れずに!
次回の内容はこちら


コメント
[…] […]
[…] […]
[…] […]