
今回は,$LC$振動回路について説明します.
入試問題でも割とよくみかけますが,とっつきにくい印象があるかもしれません.
直観的な理解の仕方もありますが,ここでは回路の式を立て,単振動の運動方程式と見比べることで,電流や電圧の時間変化を求めていきたいと思います.(微分方程式を書きますが,それを解くわけではなく,あくまでも単振動の運動方程式と比較するだけです.)
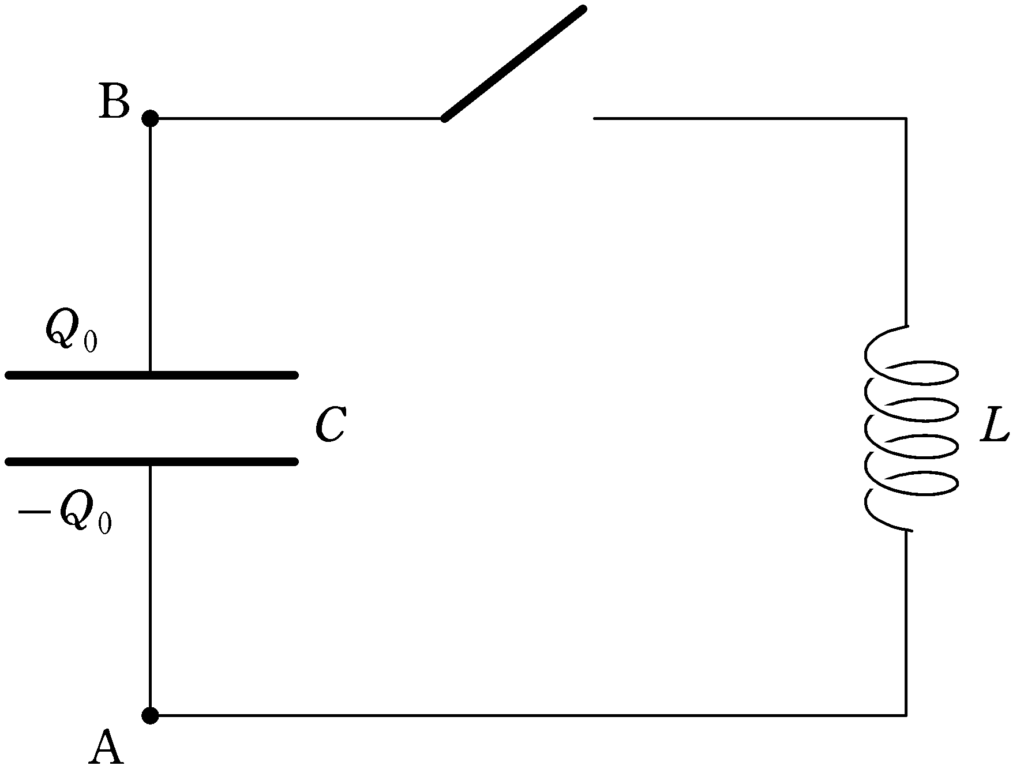

電気容量$C$のコンデンサー,自己インダクタンス$L$のコイル,スイッチを上図のようにつなげます.あらかじめコンデンサーには電荷$Q_{0}$が蓄えられているとしましょう.
Aに対するBの電位を$V$,この回路を時計回りに流れる電流を$i$とします.
時刻$t=0$でスイッチを閉じましょう.
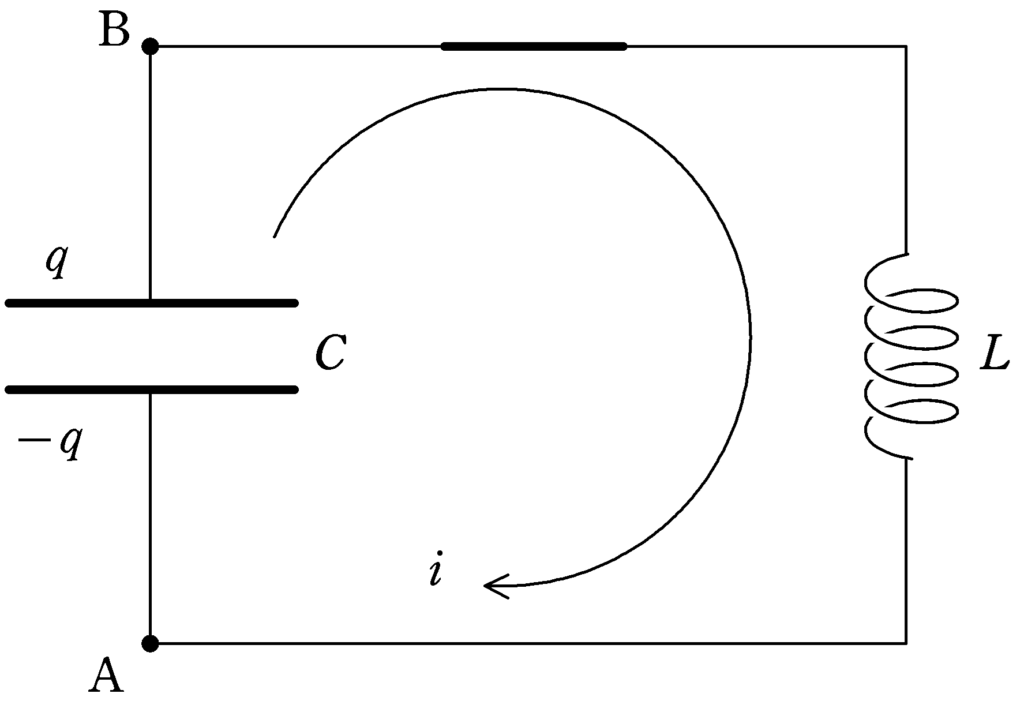

時刻$t$において,コンデンサーには電荷$q$が蓄えられています.また,回路には$i$の電流が流れているとしましょう.
まず,コンデンサーの基本式からAに対するBの電位$V$を求めます.
★ コンデンサーの基本式
$q=CV$
$\therefore V=\dfrac{q}{C}$ $\dots (\ast)$

また,コイルに電流$i$が流れると,電流が流れる向きに$-L\dfrac{di}{dt}$の起電力が生じます.
これは,回路中のコイルの問題でよく使うので確認しておいてください.
なぜ,このように「-」がつくのかは,下の記事で説明しています.
すると,$(\ast)$から,キルヒホッフ則より
★ キルヒホッフ則
$\dfrac{q}{C}-L\dfrac{di}{dt}=0$ $\dots (2\ast)$

また,時間$\varDelta t$の間にコンデンサーの電荷が$\varDelta q$変化したとき,電流$i$は次のようになります.
$i=-\dfrac{\varDelta q}{\varDelta t}$

え?なんで,「$-$」がつくの?

それは,こちらでチェックしておいてください.

今回は,微分方程式を立てたいので,$\varDelta t\to 0$として,
$i=-\dfrac{dq}{dt}$ $\dots (3\ast)$
とします.
$(3\ast)$を$(2\ast)$に代入すると
$\eqalign{\dfrac{q}{C}-L\dfrac{d}{dt}\left( -\dfrac{dq}{dt} \right)=0\cr L\dfrac{d^{2}q}{dt^{2}}=-\dfrac{1}{C}q \dots (\sharp)}$

これは,単振動の運動方程式
$ma=-kx$
の形になっているね.加速度は位置$x$の2階微分だから
$a=\dfrac{d^{2}x}{dt^{2}}$
なので,
$m\dfrac{d^{2}x}{dt^{2}}=-kx$
この単振動の角振動数$\omega$は
$\omega=\sqrt{\dfrac{k}{m}}$
だったね.
単振動を忘れてしまった人は,こちらのシリーズで演習問題があるので,確実に解けるようにしておこう.

$ L\dfrac{d^{2}q}{dt^{2}}=-\dfrac{1}{C}q $
だから,コンデンサーに蓄えられる電荷は時間$t$とともに単振動の時間変化と同様な変化をするんだね.コンデンサーにはもともと電荷$Q_{0}$が蓄えられていて,これがmaxのはずだから,スイッチを入れた直後は電荷は減るね.つまり,$\cos$型だ!
角振動数$\omega$は,
$\omega=\sqrt{\dfrac{1}{LC}}$
だから,時刻$t$におけるコンデンサーに蓄えられている電荷$q$は
$q=Q_{0}\cos\left(\dfrac{1}{\sqrt{LC}}t\right)$ $\dots (4\ast)$
になるね.

$(4\ast)$を$(3\ast)$に代入して,$i$を計算しましょう.
(三角関数の微分,合成関数の微分を使います.できない人は,次の記事で練習しておくとよいでしょう.)
$(4\ast)$を$(3\ast)$に代入して
$\eqalign{i&=-\dfrac{d}{dt}\left( Q_{0}\cos\left(\dfrac{1}{\sqrt{LC}}t\right)\right)\\&=-Q_{0} \left(\dfrac{1}{\sqrt{LC}}t \right) ^{\prime}\left\{-\sin\left(\dfrac{1}{\sqrt{LC}}t \right)\right\} \\&=\dfrac{Q_{0}}{\sqrt{LC}}\sin\left(\dfrac{1}{\sqrt{LC}}t \right)}$

$I_{0}= \dfrac{Q_{0}}{\sqrt{LC}} $とおくと
$i=I_{0} \sin\left(\dfrac{1}{\sqrt{LC}}t \right) $
となるね.

また,$(4\ast)$を$(\ast)$に代入すると電位$V$がわかります.
$(4\ast)$を$(\ast)$に代入して
$V=\dfrac{q}{C}= \dfrac{Q_{0}}{C}\cos\left(\dfrac{1}{\sqrt{LC}}t\right) $

電流も電位も単振動しているんだね.
角振動数が$\omega=\dfrac{1}{\sqrt{LC}}$
だから,周期$T$は
$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{LC}$
だね.

そうですね.
ちなみに,電流と電圧のグラフをかくと次のようになります.
赤い方は電圧(Aに対するBの電位),青い方は電流です.
電圧の最大値は$V_{0}$としています.
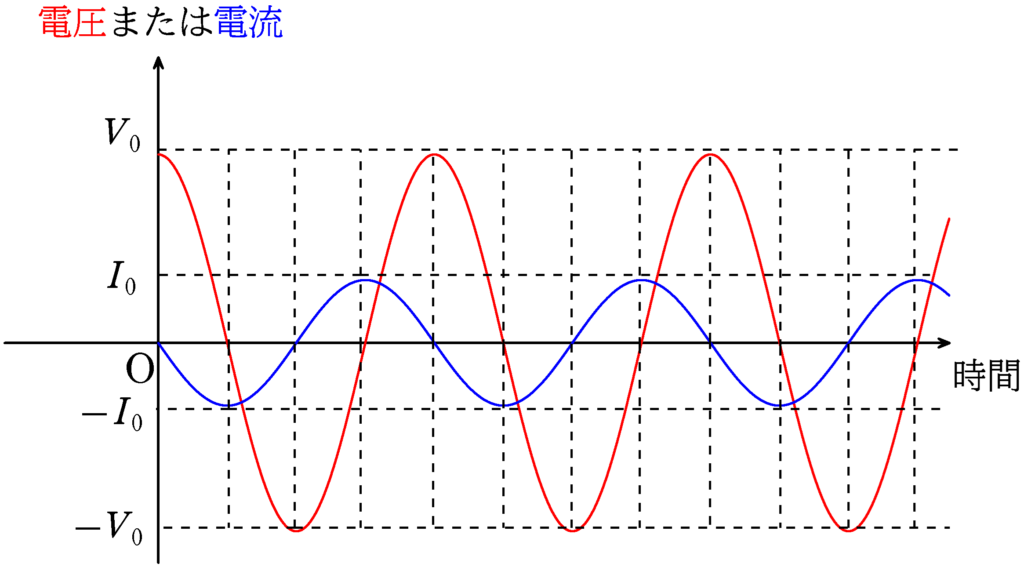

電圧の絶対値が最大になるときは,電流が0になって,電流の絶対値が最大になるときは,電圧が0になるんだね.

はい,このことは,エネルギー保存則でよく使います.
時刻$t$におけるコンデンサーの静電エネルギーとコイルの蓄えられているエネルギーの和$U$は次のようになります.
$\eqalign{U&=\dfrac{1}{2}CV^{2}+\dfrac{1}{2}Li^{2}\\&=\dfrac{1}{2}C\left\{ \dfrac{Q_{0}}{C}\cos\left(\dfrac{1}{\sqrt{LC}}t\right) \right\}^{2}+\dfrac{1}{2}L\left\{ \dfrac{Q_{0}}{\sqrt{LC}}\sin\left(\dfrac{1}{\sqrt{LC}}t \right) \right\}^{2}\\&=\dfrac{Q_{0}^{2}}{2C}\left\{\cos^{2} \left(\dfrac{1}{\sqrt{LC}}t\right) +\sin^{2} \left(\dfrac{1}{\sqrt{LC}}t\right) \right\}\\&=\dfrac{Q_{0}^{2}}{2C}}$

$\cos^2 (\omega t)+\sin^{2}(\omega t)=1$だから,$U$は時間に依らず一定になるんだね.

具体的な$LC$振動回路の問題は別にやりますが,ここでは,次のことを確認しておきましょう.
- 電荷,電流,電圧はそれぞれ単振動する.
- $\dfrac{1}{2}CV^{2}+\dfrac{1}{2}Li^{2}=$一定になる.
を確認しておきましょう.
※ ちなみに,今回は$q$の微分方程式から導きましたが,$(\ast)$~$(3\ast)$を$i$や$V$の微分方程式の形にすると
$L\dfrac{d^{2}i}{dt^{2}}=-\dfrac{i}{C}$
$L\dfrac{d^{2}V}{dt^{2}}=-\dfrac{V}{C}$
となり,いずれも同じ微分方程式となります.







コメント
[…] 直列合成すると,前回の内容と同様に考えることができます. […]
[…] $LC$振動回路 回路の式を立て,単振動の運動方程式と見比べるPHYさん今回… […]
お世話になっています。
上から2個目の図のコンデンサーの下側の-qたまっている極板に対して同じように考えると、
キルヒホッフの第二法則より
(q/c)-L(di/dt)= 0
電流が流れ込んでいる向きなので
i=dq/dt
になると思ったのですがこのまま計算を進めていくとy=Kxの形になってしまい-Kxの形になりません。示されている上側の極板に着目するやり方となぜ違うのか教えて欲しいです。
質問ありがとうございます。
今回も,図が必要のため,直接メールさせてもらいました.