入試にも頻出である運動量保存則.この法則が出てくるときは問題が難しいことも多いです.しかし,いつでも運動量保存則が使えるわけではありません.
今回は,運動量保存則が使える条件について考えていきましょう.
※ 最後にまとめがかかれているので,運動量が保存する条件を確認したいだけの人はそこまでまでとんでください.
運動量とは
物体の質量を$m$,速度を$v$とすると,運動量は$mv$で表されます.$v$は速度で,ベクトル量であることから,運動量はベクトル量であることがわかります.つまり,計算するときは,ベクトル計算をする必要があります.ほとんどの問題は運動方程式と同様に,水平成分と鉛直成分などのように,各成分に分けて計算をします.
また,運動量$mv$の質量$m$が大きいと運動量は大きいです.たとえば,同じ速さでもビー玉が向かってくるのと,トラックが向かってくるのでは全然勢いが違います.そう,運動量は”運動の勢い”を表しています.ただし,この勢いのは向きがあります.“向きを含んだ勢い”が運動量のイメージです.
そもそも運動量保存則はどういうときに使うの?
高校物理の問題を解く際に,意識してことがあります.それは,
その公式はどのようなときに使うのか
です.これをある程度頭に入れておかないと,方針が経たずに時間が過ぎてしまいます.
それでは,運動量保存則はどのような問題で使うのでしょうか?それは,
2つ以上の物体が運動しているとき
です.運動量保存則はその性質から1つの物体の運動で使うことはまずありません.問題で2つ以上の物体が運動していたら,””もしかしたら運動量保存則を使うかも..”と思ってください.
運動量保存則が使える条件
しかし,2つの物体が運動しているからといって,いつでも運動量保存則が使えるとは限りません.使える条件があるのです.その説明は後にするとして,まずは,使用条件を確認しておきます.それは
運動量保存則を立てる成分の物体にはたらく力の和が0のとき
このような条件からほとんどの問題は水平方向のみ運動量保存の式を立てます.(のちに述べるように,鉛直方向でも運動量が保存することもあります.)
なぜ,ではなぜ鉛直方向の運動量保存の式を立てることが少ないのでしょうか.その理由は2つです.
- 鉛直方向は運動しないいのです,わざわざ運動量保存則を立てる必要がない.
- 鉛直方向は運動量が保存しない.
これらのことを考えるためにも,そのそも運動量保存則はどのように導出するのかを考えていきましょう.
運動量保存則の導出
運動量保存則は運動方程式から導出できます.次の2つの物体が運動しているときの運動方程式を考えていきましょう.
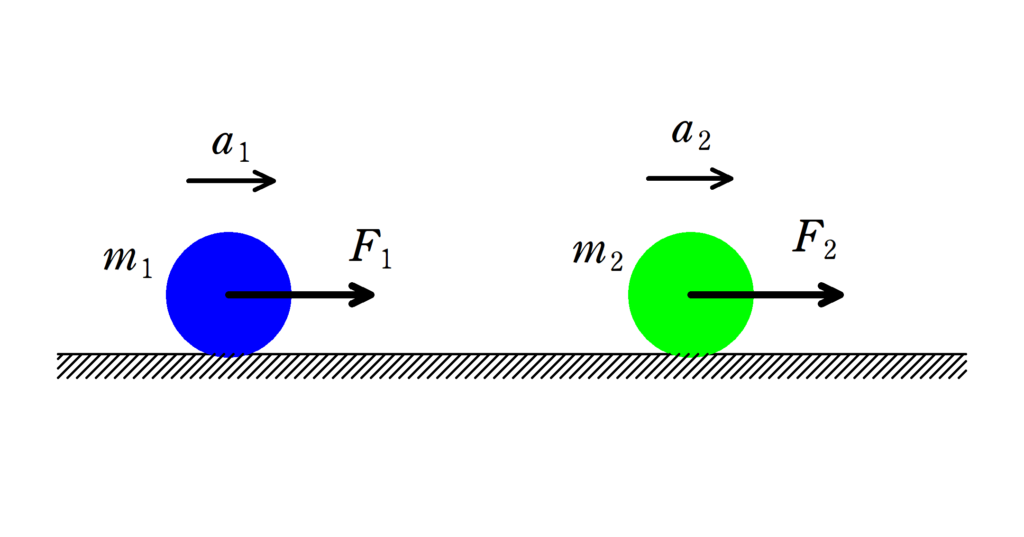
青い物体と緑の物体の質量をそれぞれ,質量が$m_{1}$,$m_{2}$,はたらく力をそれぞれ$F_{1}$,$F_{2}$,加速度をそれぞれ$a_{1}$,$a_{2}$とします.それぞれの運動方程式は
$m_{1}a_{1}=F_{1}$,$m_{2}a_{2}=F_{2}$ ($\ast$)
また,加速度の定義から,$\varDelta{t}$の間の青と緑の物体それぞれの速度の変化を$\varDelta{v_{1}}$,$\varDelta{v_{2}}$とすれば
$a_{1}=\dfrac{\varDelta v_{1}}{\varDelta t_{1}}$,$a_{2}=\dfrac{\varDelta v_{2}}{\varDelta t_{2}}$
であるから,($\ast$)に代入して
$m_{1} \dfrac{\varDelta v_{1}}{\varDelta t_{1}}=F_{1} $,$m_{2} \dfrac{\varDelta v_{2}}{\varDelta t_{2}}=F_{2} $,
さらにこの式の両辺に$\varDelta t$をかけて
$m_{1} \varDelta v_{1}=F_{1} \varDelta t_{1}$,$m_{2} \varDelta v_{2}=F_{2} \varDelta t_{2}$ ($2 \ast$)
この式の左辺は運動量の変化,右辺は力積を意味しています.これは運動方程式同様に因果関係を表していて,
力を一定時間加える(力積が原因)ことで,運動量が変化(結果)する
という意味であることも覚えておきましょう.さて,($2 \ast$)の2式を足していくと
$m_{1} \varDelta v_{1}+m_{2} \varDelta v_{2}=(F_{1}+F_{2}) \varDelta t_{1}$ ($3 \ast$)
さて,仮に($3 \ast$)の右辺の$F_{1}+F_{2}=0$であるとき,右辺が0となるから左辺も$0$となります.ここで,$\varDelta v_{1}=v’_{1}-v_{1}$,$\varDelta v_{2}=v’_{2}-v_{2}$とすると
$m_{1}(v’_{1}-v_{1})+m_{2}(v’_{2}-v_{2})=0$
$m_{1}v_{1}+m_{2}v_{2}=m_{1}v’_{1}+m_{2}v’_{2}$
この式がよく知られている運動量保存則の形です.
再び!運動量保存則が使える条件
さて,運動量保存則は($3 \ast$)から特別な条件を代入した結果導出されました.その特別な条件とは
$F_{1}+F_{2}=0$ つまり 力の和が0
です.だから,運動量保存則が使えるのは力の和が0のときなんです.
力の和が0の問題なんてめったにないと思うかもしれませんが,物体に作用反作用の力だけがはたらいていれば,運動量が保存します.
そして,鉛直方向の運動量が保存しない利用は重力がはたらくからです.重力の反作用は地球なので,地球まで物体系に入れれば運動量は保存しますが,日常の物理で地球を対象として考える問題はほとんどありませんね...
力の和が0ではなくても運動量保存則を立てるとき
実は,運動量保存則は力の和が0ではなくても立てることができます.($3 \ast$)からわかるように,$F_{1}+F_{2}$が0でなくても,$\Delta t=0$であればいいんです.いや,正確にいうと,$\Delta t\fallingdotseq 0$のとき,つまり,非常に短い間に関する運動量保存則を立てるときです.この1つに”衝突問題”があります.
衝突問題では多少の外力がはたらいても力積は0とみなすことができ,その結果運動量保存則を立てることができる.
多少の外力とは・・・?ここが難しいところです.いくら$\Delta t$が0に近くてもあまりにも$F_{1}+F_{2}$が大きいと力積は0とみなせなくなり,その結果運動量は保存しません.それでは,どのような力がはたらくときは衝突前後で運動量が保存し,どのようなときには運動量が保存しないのかをまとめておきます.
- 重力,弾性力,動摩擦力など→運動量が保存する
- 物体をおさえるけるような力がはたらく→運動量が保存しない
具体的に図で確認てみましょう.
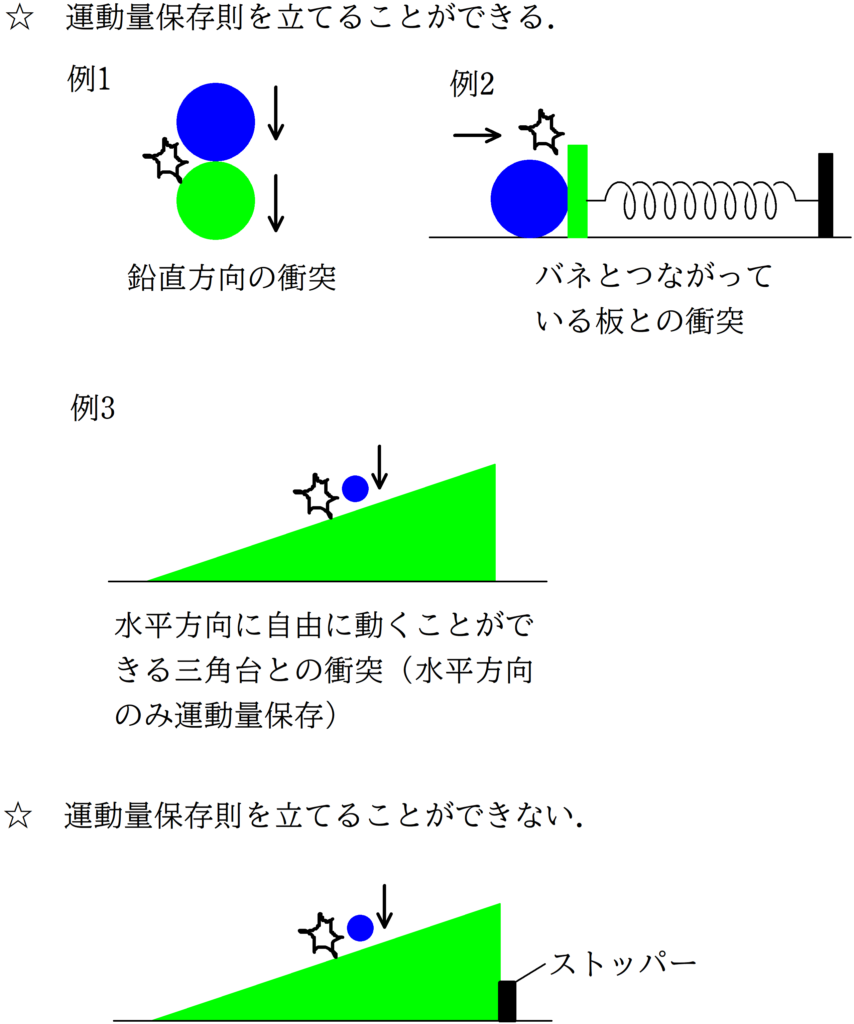
上図のように,ストッパーがかかっていると,三角台にストッパーから非常に大きな力がはたらくので,運動量は保存しません.上図の例1のようなタイプの問題は”すっとびボールの問題”などが例にあります.例2はばねが自然長であるときを考え,実はそもそもまだ弾性力がはたらいていません.
まとめ
- 運動量保存則は2つ以上の物体が運動しているときに立てる.
- 運動量が保存する条件は力の和が0のときで,水平方向の運動量保存則を立てることが多い.
- 多少に外力がはたらいても,衝突の直前後であれば運動量が保存することがある.特に,空中で衝突がある.
- ストッパーや壁,床などのおさえつけるような力がはたらくときは運動量が保存しない.
運動量保存則を立てることができるようになると,やや難しい問題に対応することができます.問題を解く際に,運動量が保存するかしないかを確認する癖をつけるとよいでしょう.最後に,注意点です.今までのことから,運動量の速度$v$は慣性系からの速度の方がよいでしょう.加速度運動している観測者からみると,慣性力がはたらき,力の和が0にならないことが多いからです.




コメント
[…] 力学的エネルギー保存則は運動量保存則とともに,保存則を立てることができるのかを確認しないといけません.式が成り立たないのに,勝手に立式したのでは×になりますからね.この記事でも述べたように,運動量保存則が成り立つ条件は物体系にはたらく力の和が0であることでした.それでは,力学的エネルギーが保存する条件はどうでしょうか?この話をする前に,次の問題を考えてみましょう. […]
[…] 運動量保存則が使える条件とは!? […]
[…] […]