
今回は未知な起電力を求める問題を扱います.
この問題を解く際,次のことを知っておきましょう.
長さ$l$,断面積$S$,抵抗率が$\rho$の電気抵抗の抵抗値$R$は
$R=\rho \dfrac{l}{S}$
※ 長い抵抗ほど,抵抗値が大きい.断面積が大きいと抵抗値は小さい.
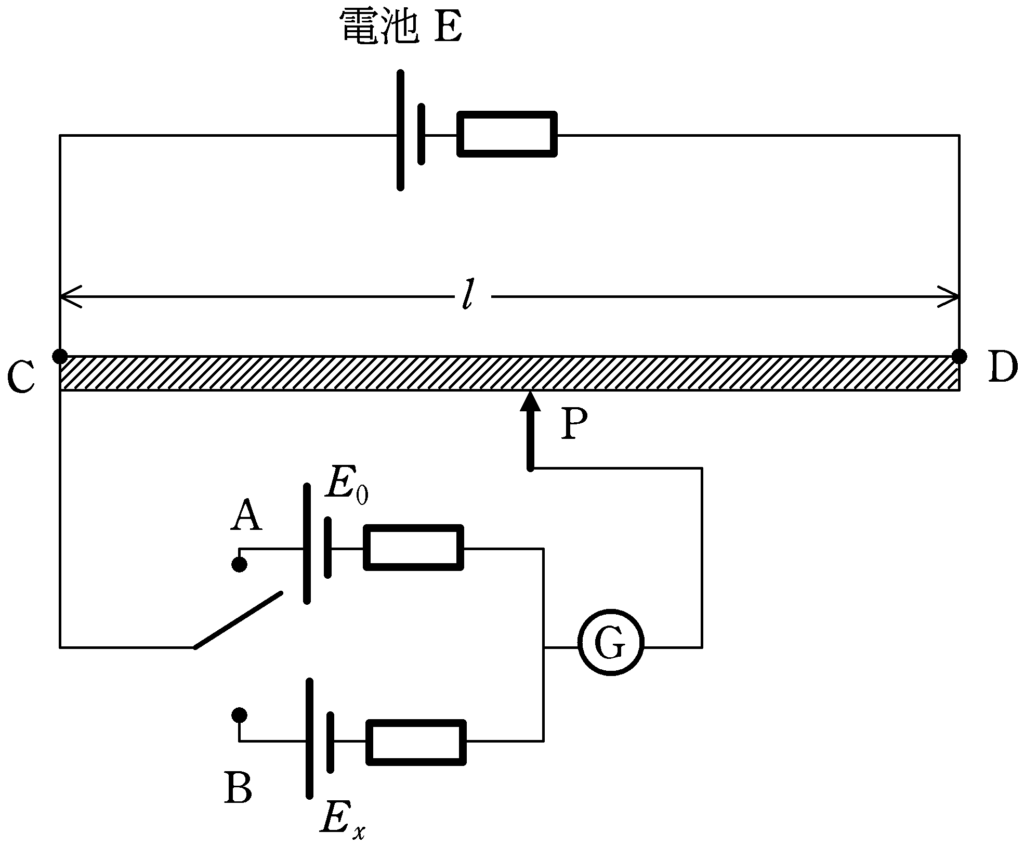
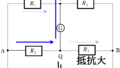
上図のように,電池E(この電池の起電力は使用しないで,具体的な値はかかない.)と起電力$E_{0}$,$E_{x}$の電池,長さ$l$で抵抗値$R$の一様な抵抗線CD,スイッチ,検流計がある.
次の①,②を行うことで,未知な起電力$E_{x}$を求める.
①:スイッチをAにつなぎ,接触子Pを移動させ,検流計の針が触れない位置を探した.このとき,CP$=l_{1}$であった.
②:次にスイッチをBにつなぎ,接触子Pを移動させ,検流計の針が触れない位置を探した.このとき,CP=$l_{2}$であった.
このとき,次の問いに答えよ.
(1) ①について,抵抗Rに流れる電流を$I$とする.$E_{0}$を$R$,$l$,$l_{1}$,$I$を用いて表せ.
(2) ②について,抵抗Rに流れる電流を$I$とする.$E_{x}$を $R$,$l$,$l_{2}$,$I$を用いて表せ.
(3) (1),(2)より,$E_{x}$を$E_{0}$,$l_{1}$,$l_{2}$を用いて表せ.
<解答>
(1)
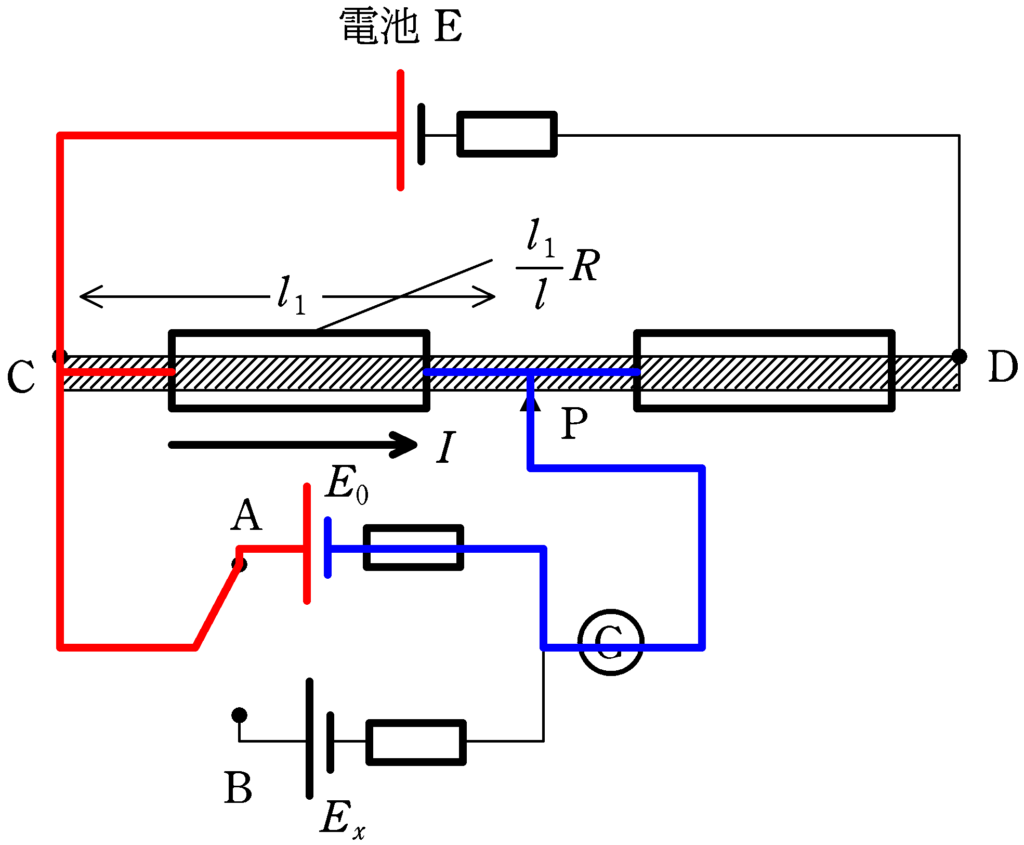

検流計に電流が流れていないので,起電力$E_{0}$の電池の内部抵抗が仮にあったとしても,内部抵抗で電位は落ちずにCP間の電位差は$E_{0}$(どちらも赤と青の電位差)となるね.
また,抵抗は長さに比例するので,CP間の抵抗を$R_{1}$とすると
$R:R_{1}=l:l_{1}$
$\therefore R_{1}=\dfrac{l_{1}}{l}R$
になるね.
CP間の電位差が$E_{0}$,抵抗が$\dfrac{l_{1}}{l}R$,電流が$I$なので,オームの法則より,次の関係が成り立ちます.
★ オームの法則
$E_{0}=\dfrac{l_{1}}{l}R\cdot I$ $\cdots (\ast)$ (答)
(2)
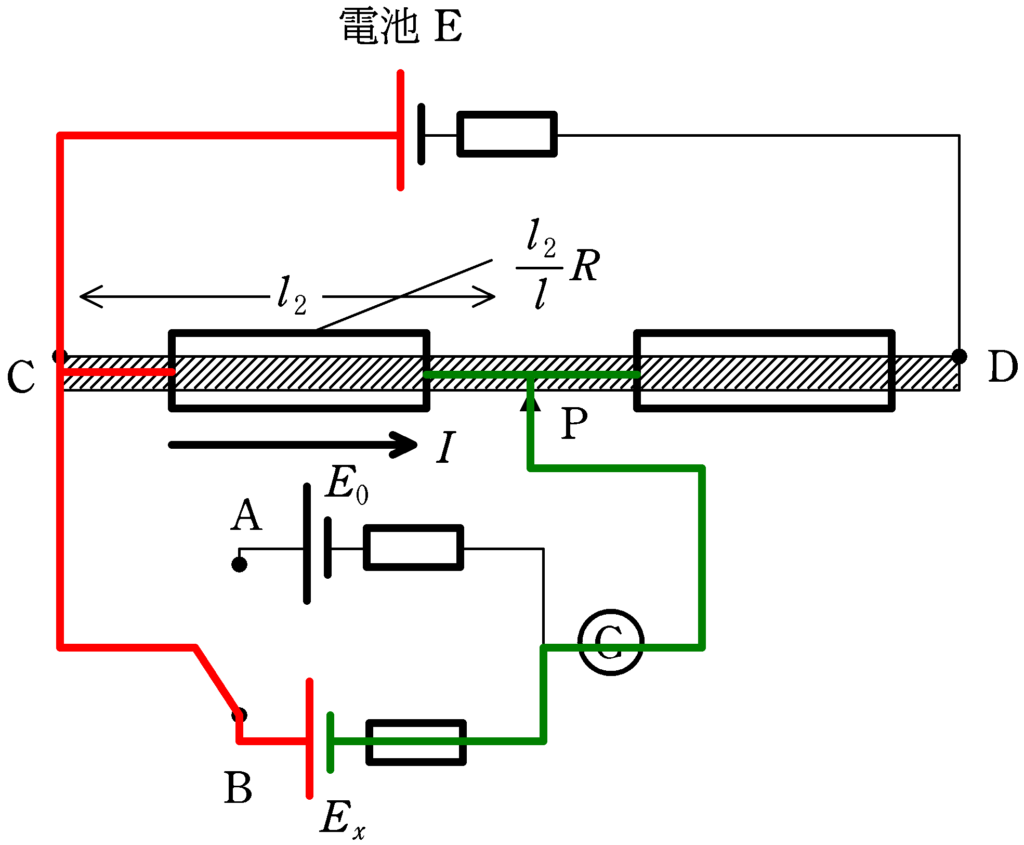

今回も,検流計に電流が流れていないので,CP間の電位差(赤と緑の差)は$E_{x}$です.
また,今回も(1)で考えたときのCD間に流れる電流と全く同じ電流が流れます.
なぜかというと,(1)と(2)どちらも,電池Eと,CD間の抵抗と,電池Eの内部抵抗の回路になっているからです.(検流計に電流を流さないようにしているのがここで効いています.)
また,抵抗は長さに比例するので,CP間の抵抗を$R_{2}$とすると
$R:R_{2}=l:l_{2}$
$\therefore R_{2}=\dfrac{l_{2}}{l}R$
になるね.
CP間の電位差が$E_{x}$,抵抗が$\dfrac{l_{2}}{l}R$,電流が$I$なので,オームの法則より,次の関係が成り立ちます.
★ オームの法則
$E_{x}=\dfrac{l_{2}}{l}R\cdot I$ $\cdots (2\ast)$ (答)
(3) (1)(2)で求めた$(\ast),(2\ast)$より,$I$を消去します.
$(\ast)$より
$I=\dfrac{E_{0}l}{Rl_{1}}$ $(3\ast)$
$(2\ast)$より
$I=\dfrac{E_{x}l}{Rl_{2}}$ $(4\ast)$
$(3\ast)$,$(4\ast)$より
$ \dfrac{E_{x}l}{Rl_{2}} = \dfrac{E_{0}l}{Rl_{1}} $
$\therefore E_{x}=\dfrac{l_{2}}{l_{1}}E_{0}$ (答)

この結果を見ると,未知な起電力$E_{x}$は,検流計に電流が流れないときCP間の長さ$l_{1} , l_{2}$を測定して,あらかじめ知っている起電力$E_{0}$を用いて計算ができることになりますね.
また,これは,$E_{x}$の内部抵抗があろうとなかろうと計算ができます.
理由は,検流計に電流が流れないときを考えているからです.つまり,電流が流れないので,内部抵抗では電位が落ちないので,まったく関係ありません.

コメント