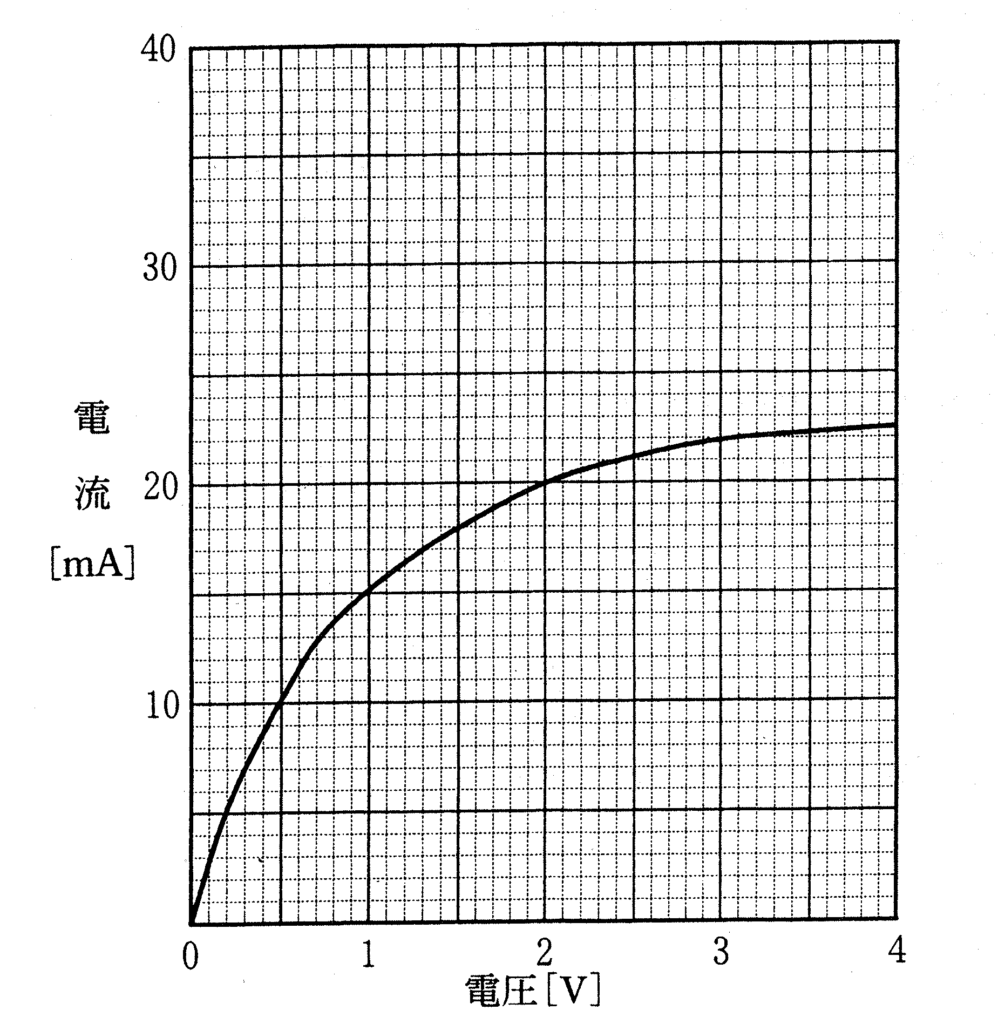
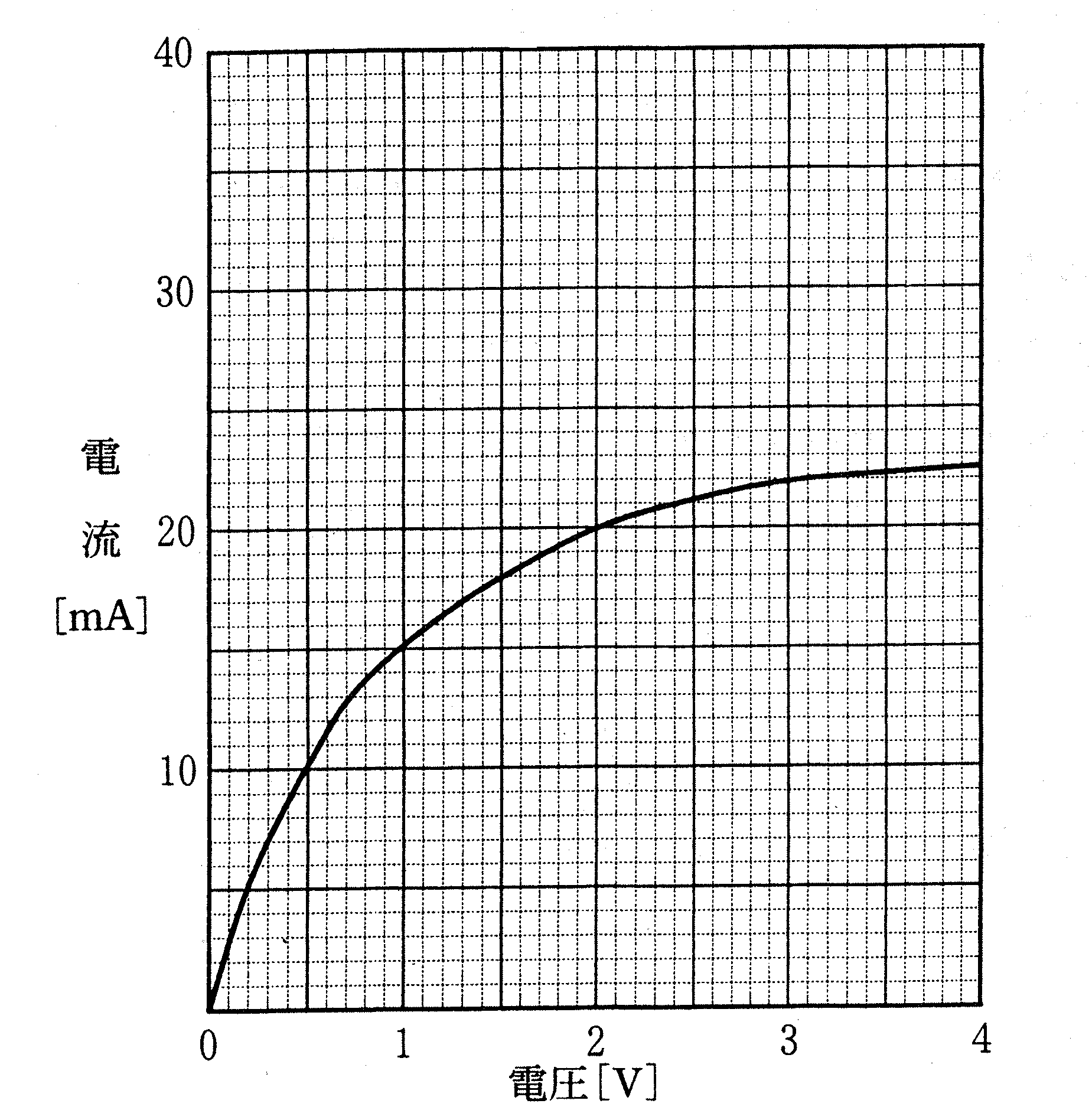
図のような電流-電圧特性をもつ抵抗Aがある.
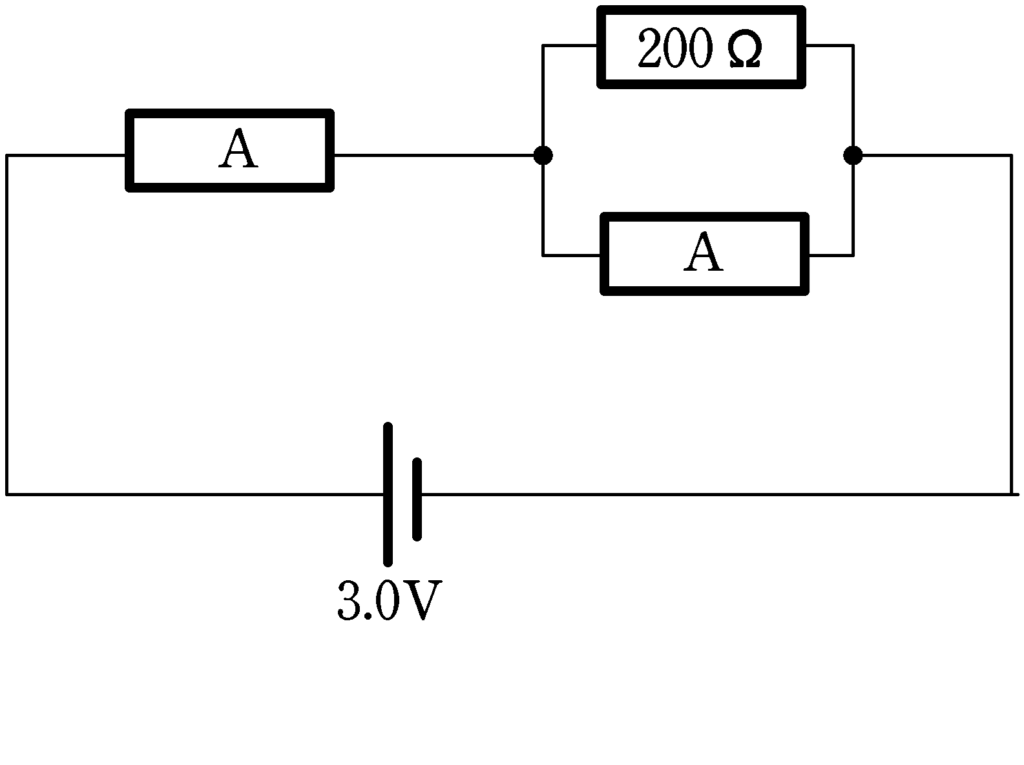
下図のように,2つの抵抗A,$200\Omega$の抵抗R,および起電力が$3.0\rm V$の内部抵抗の無視できる電池からなる回路をつくった.このとき,抵抗Rに流れる電流を求めなさい.
<解答>
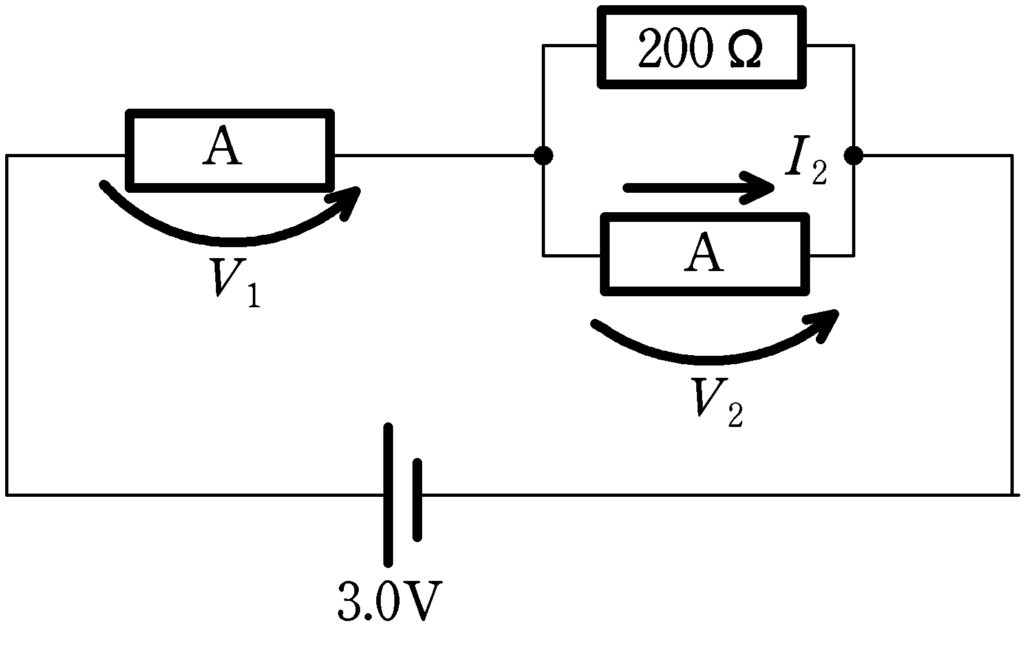

まずは,右側の抵抗Aに流れる電流を$I_{2}[\rm mA]$,かかる電圧を$V_{2}[\rm V]$,左側の抵抗Aにかかる電圧を$V_{1}[\rm V]$と文字の設定をしましょう.
特性曲線の問題は,このように“特性をもつ抵抗の電流電圧の設定”からはじめることが多いね.
※ 左側の電流Aはキルヒホッフ第1法則から計算できるので,文字の設定を行いませんでした.
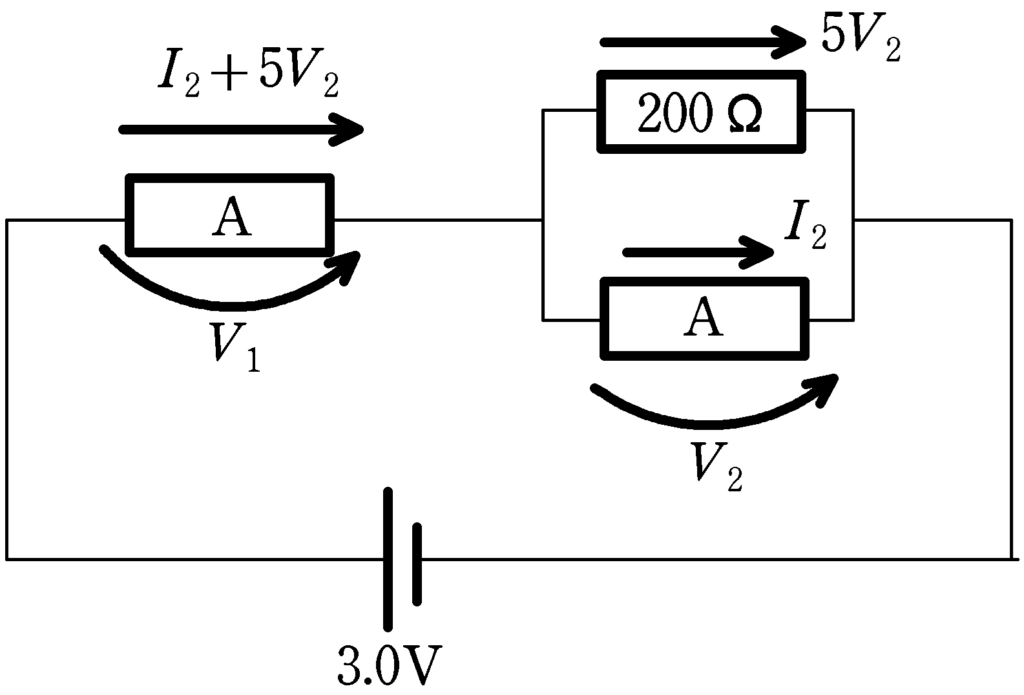

特性曲線のグラフの縦軸の電流の単位が$\rm mA$なので,これに合わせていきます.
$200\Omega$の抵抗にかかる電圧が$V_{2}[\rm V]$なので,オームの法則より
$\dfrac{V_{2}}{200} [\rm A]$
の電流が流れますが,これを$\rm mA$になおすと,上の値を1000倍して
$5V_{2}[\rm mA]$
となります.これは,$2\rm A$の電流は$2000\rm mA$であるという計算と同じです.
すると,キルヒホッフ第1法則より,左側の抵抗Aに流れる電流は
$I_{2}+5V_{2}[\rm mA]$
となります.

しかし,この後,どうすればいいかわからなくなってしまいます.特性曲線をどう使えばいいのかわからなくなってしまいます.
そこで,特性曲線をグラフではなく,式として与えられていると考えましょう.
例えば,$y=x^{2}$の2次関数のグラフだったら,$f(x)=x^{2}$として,$y=f(x)$と表すように,今回は特性曲線のグラフを
$i=f(v)$
と表します.
このとき,左側の抵抗Aにかかる電圧は$V_{1}$で,流れる電流が$I_{2}+5V_{2}$なので
$I_{2}+5V_{2}=f\left(V_{1}\right)$ $\cdots (\ast)$
とかくことができ,右側の抵抗Aにかかる電圧は$V_{2}$で,流れる電流が$I_{2}$なので,
$I_{2}=f\left(V_{2}\right)$ $\cdots (2\ast)$
とかくことができます.
$(\ast)$と$(2\ast)$をみると,$V_{1}$が邪魔なので,キルヒホッフ第2法則から$V_{1}$を消去しましょう.
$V_{1}+V_{2}=3.0$
$\therefore V_{1}=3-V_{1}$
これを$(\ast)$に代入して
$I_{2}+5V_{2}=f\left(3-V_{2}\right)$ $\cdots (\ast)’$
となります.つまり,$(\ast)’$と$(2\ast)$より
$I_{2}= f\left(3-V_{2}\right) -5V_{2}$
と
$I_{2}=f\left(V_{2}\right)$
の2つの曲線の交点を調べれば$I_{2}$と$V_{2}$が出てきます.

$I_{2}=f\left(V_{2}\right)$はもともとかかれている特性曲線のグラフなので,よいでしょう.
$I_{2}=f\left(3-V_{2}\right) -5V_{2}$については,まず$f(3-V_{2})$のグラフを考えていきましょう.
$f(-V_{2})$は,$f(V_{2})$を縦軸に関して対称移動したグラフです.さらに,
$f(3-V_{2})=f(-(V_{2}-3))$
なので,$f(3-V_{2})$は,$f(-V_{2})$のグラフを横軸方向に$3$だけ正方向に平行移動したグラフになります.(下図青色の曲線)
さらに,$ f\left(3-V_{2}\right) -5V_{2} $の$-5V_{2}$に関しては例えば,
$V_{2}=2.0[\rm V]$のとき,$-5V_{2}=-5\times 2.0=-10[\rm V]$
$V_{2}=1.5[\rm V]$のとき,$-5V_{2}=-5\times 1.5=-7.5[\rm V]$
$V_{2}=1.0[\rm V]$のとき,$-5V_{2}=-5\times 1.0=-5.0[\rm V]$
のように具体的に計算し,青の曲線のグラフから縦軸方向に引いていき,グラフを完成します.下図のオレンジ色のグラフが$I_{2}=f(3-V_{2})-5V_{2}$です.
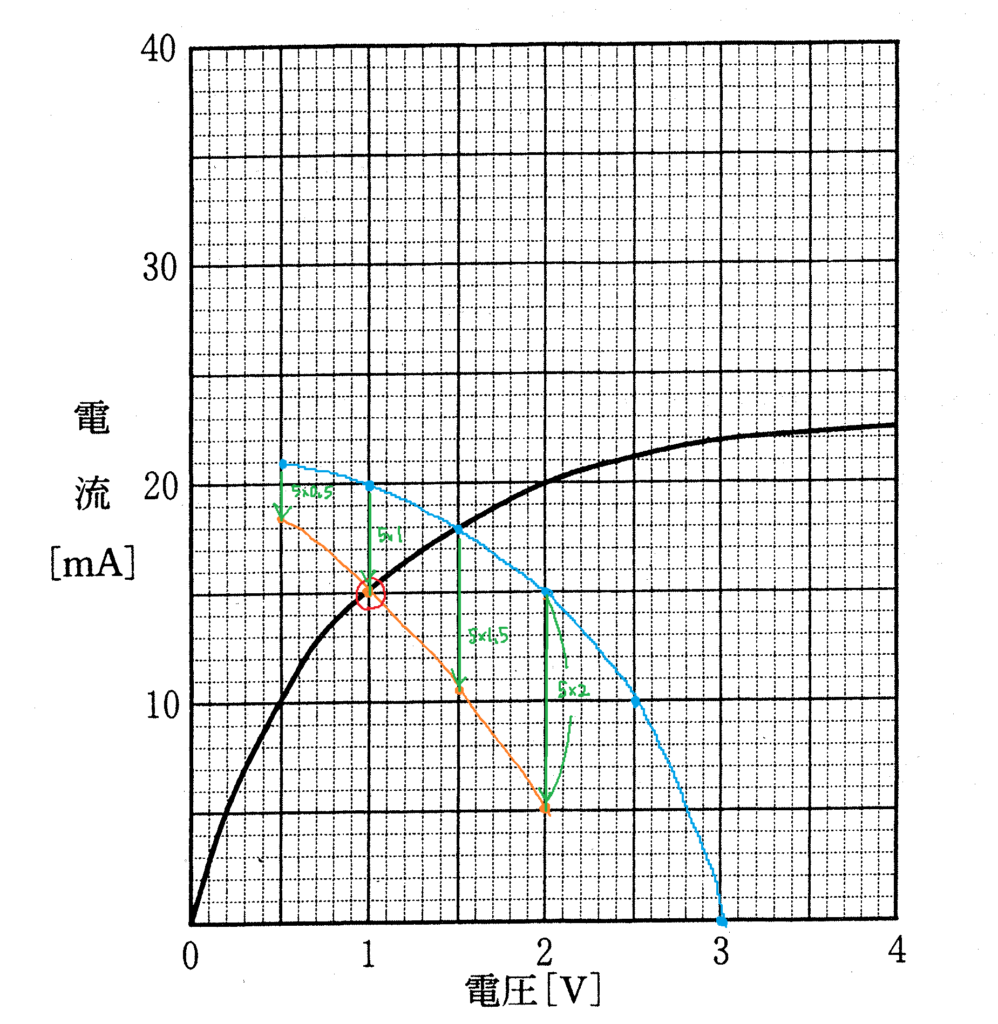

$I_{2}=f(V_{2})$(上図黒の曲線)と,$I_{2}=f(3-V_{2})-5V_{2}$(上図オレンジ色の曲線)の交点を調べれば,$V_{2}=1.0[\rm V]$,$I_{2}=15[\rm mA]$となります.
すると,$200\Omega$の抵抗にかかる電圧も$1.0[\rm V]$なので,オームの法則より,流れる電流は
$\dfrac{1.0}{200}=5.0\times 10^{-3}[\rm A]$ (答)
または,$5.0[\rm mA]$ (答) を得ます.


コメント