
サルが木から落ちた瞬間,銃を撃ったとしましょう.このとき,弾丸がサルに当たるためには,銃をどのような角度に向ければいいか??
ただ,サルがあまりにもかわいそうなので,今回は十分小さい球を初速度0で落とした瞬間に銃で撃つことを考えましょう.
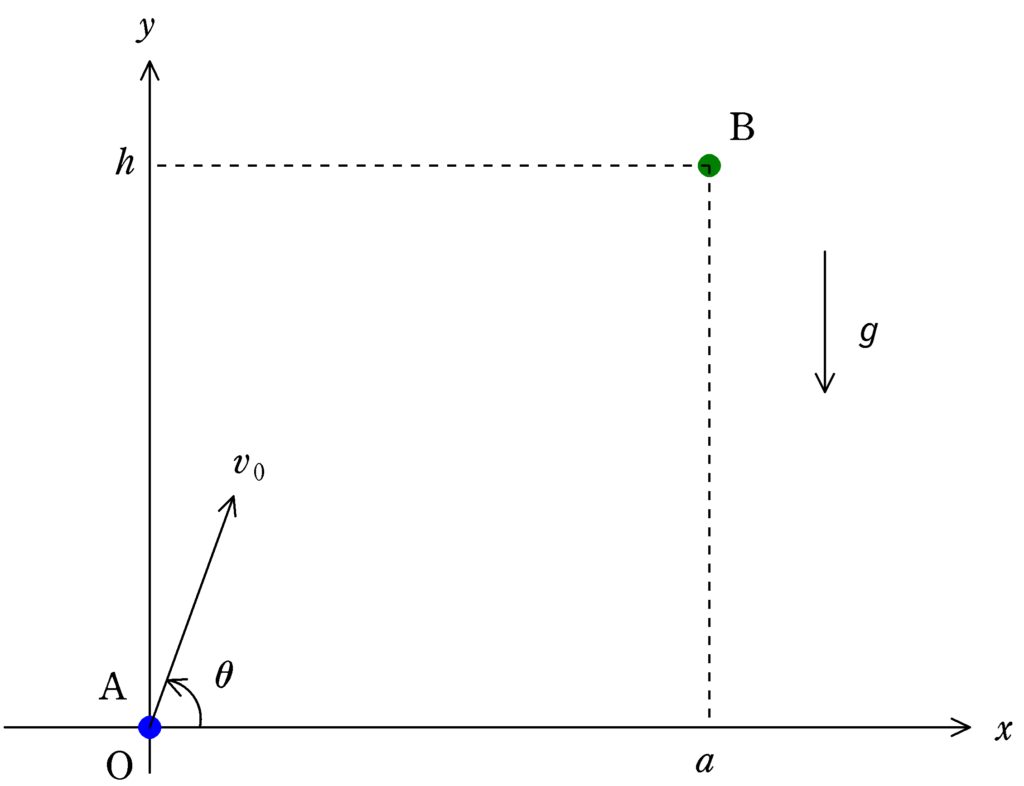
上図のような$xy$直交座標の原点Oに質点Aを,座標$(a , h)\,(a , h>0)$に質点Bを固定する.$y$軸の正の向きを鉛直上向きとし,$t=0$で$x$軸正方向より,反時計回りに角度$\theta\,\left(0<\theta<\dfrac{\pi}{2}\right)$の方向に速さ$v_{0}$の初速度を与える.これと当時に$t=0$において質点Bの固定をはずし,自由落下させる.次の問いに答えよ.ただし,重力加速度の大きさを$g$とする.また,空気抵抗は無視できるとする.
(1) 時刻$t$における質点Aの座標$(x_{\rm A} , y_{\rm A})$と質点Bの座標$(x_{\rm B} , y_{\rm B})$をそれぞれ求めよ.
(2) 質点Aの初速度を与えた角度$\theta$を調整すると,質点Aと質点Bが衝突した.ただし,質点Aと質点Bは水平面より十分高いところにあり,水平面とは衝突をしないものとする.衝突したときの$\tan\theta$を,$a , h$を用いて表せ.
<解答>

今回,質点A,Bにはたらく力は重力のみなので,それぞれの物体は等加速度運動をします.
等加速度運動の式を確認しましょう.
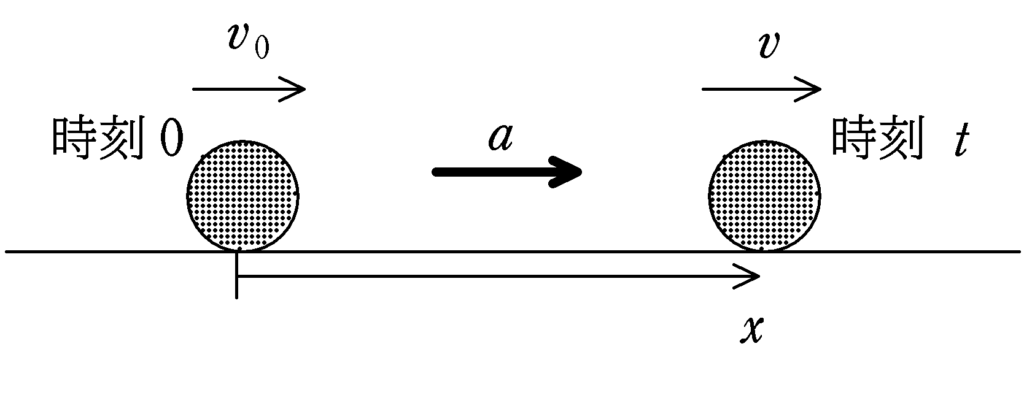
時刻$0$における速度(初速度)を$v_{0}$,時刻$t$における速度を$v$.
また,時刻$0$からの変位を$x$とする.物体が加速度$a$で等加速度運動をしているとき,次の式が成り立つ.
$v=v_{0}+at$ $\cdots (\ast)$
$x=v_{0}t+\dfrac{1}{2}at^{2}$ $\cdots (2\ast)$
また,$(\ast)$,$(2\ast)$から$t$を消去すると
$v^{2}-v_{0}^{2}=2ax$ $\cdots (3\ast)$

質点Aと質点Bの初速度,加速度,初期位置を調べましょう.
Bの初速度は0なので,いいのですが,Aは$x$方向と$y$方向に分解します.
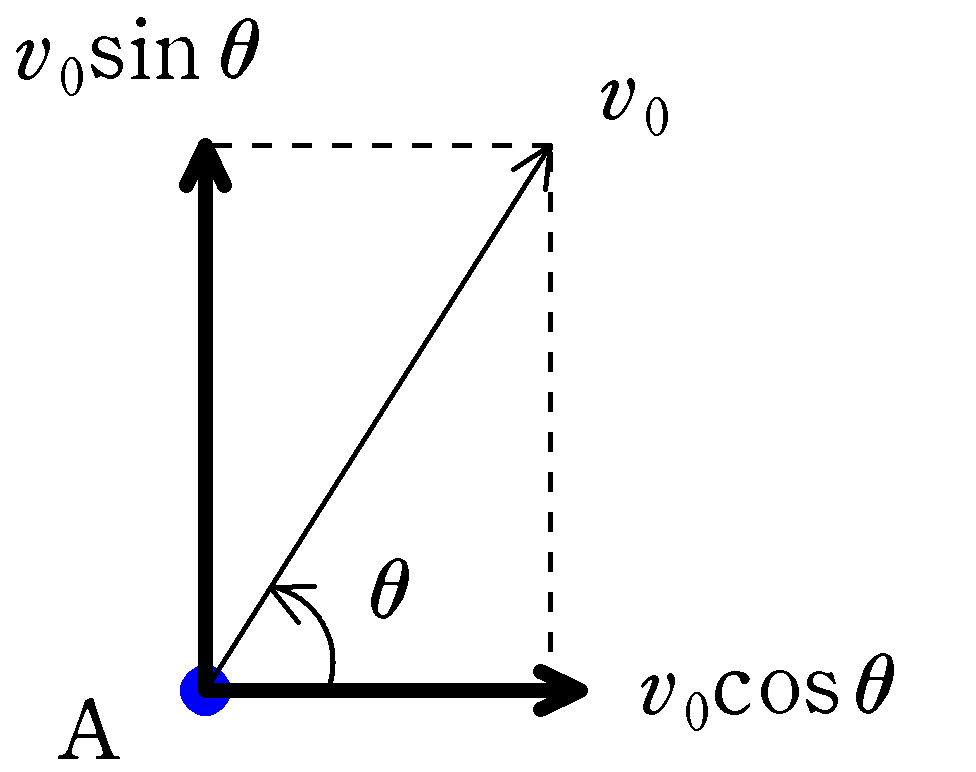

Aの$x$方向の初速度は$v_{0}\cos\theta$,$y$方向の初速度は$v_{0}\sin\theta$となります.
また,A,Bともに$x$方向には力がはたらかないため,$x$方向の加速度は0.$y$方向は$y$軸の負の向きに重力がはたらくので,$y$方向の加速度は$-g$です.
最後に,Aは$t=0$で原点にあるので,初期位置は$x$座標も$y$座標も0,Bの初期位置は問題文に書かれているように,$x$座標は$a$,$y$座標は$h$です.
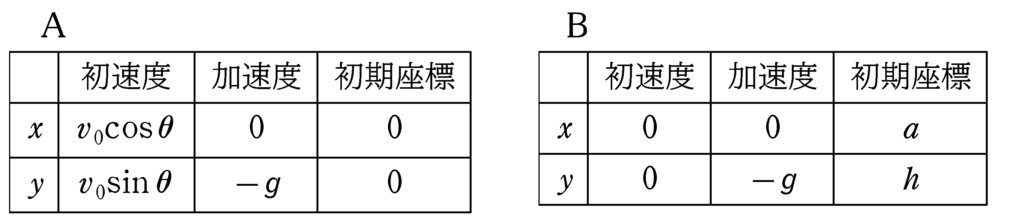

質点Aと質点Bの等加速度運動の変位の式から座標を求めます.
初期位置に変位を足したものが座標となります.
★ Aの等加速度運動の変位の式から座標$(x_{\rm A} , y_{\rm A})$を求めると
$x_{\rm A}=v_{0}\cdot (\cos\theta)\cdot t$
$y_{\rm A}=v_{0}\cdot (\sin\theta)\cdot t+\dfrac{1}{2}\cdot (-g)\cdot t^{2}$
★ Bの等加速度運動の変位の式から座標$(x_{\rm B} , y_{\rm B})$を求めると
$x_{\rm B}=0\cdot t+\dfrac{1}{2}\cdot 0\cdot t^{2}+a=a$
$y_{\rm B}=0\cdot t+\dfrac{1}{2}\cdot (-g)\cdot t^{2}+h$

以上より,
$(x_{\rm A} , y_{\rm A})=\left( v_{0}\cdot (\cos\theta)\cdot t , v_{0}\cdot (\sin\theta)\cdot t-\dfrac{1}{2}gt^{2} \right)$ (答)
$(x_{\rm B} , y_{\rm B})=\left(a , -\dfrac{1}{2}gt^{2}+h\right)$ (答)
(2)

「衝突」するので,座標が一致します.(1)で得た式において
$x_{\rm A}=x_{\rm B}$ かつ $y_{\rm A}=y_{\rm B}$
より
★ $x_{\rm A}=x_{\rm B}$
$ v_{0}\cdot (\cos\theta)\cdot t = a$ $\cdots (\sharp)$
★ $y_{\rm A}=y_{\rm B}$
$ v_{0}\cdot (\sin\theta)\cdot t\cancel{-\dfrac{1}{2}gt^{2}} = \cancel{-\dfrac{1}{2}gt^{2}}+h $
$\therefore v_{0}\cdot (\sin\theta)\cdot t=h$ $\cdots (2\sharp)$

$(\sharp)$と$(2\sharp)$から$t$を消去します.
$\dfrac{(2\sharp)}{(\sharp)}$を計算しましょう.
★ $\dfrac{(2\sharp)}{(\sharp)}$
$\dfrac{ \cancel{v_{0}}\cdot (\sin\theta)\cdot \cancel{t} }{ \cancel{v_{0}}\cdot (\cos\theta)\cdot \cancel{t} }=\dfrac{h}{a}$
$\therefore \tan\theta=\dfrac{h}{a}$ (答)

つまり,銃口は質点Bに向けておくといいんだね.



コメント
[…] […]