導体棒のグラフ対策4 電流の時間変化 | Physicmath（フィジクマス）

PHYさん

前回の内容はこちらです．

問題

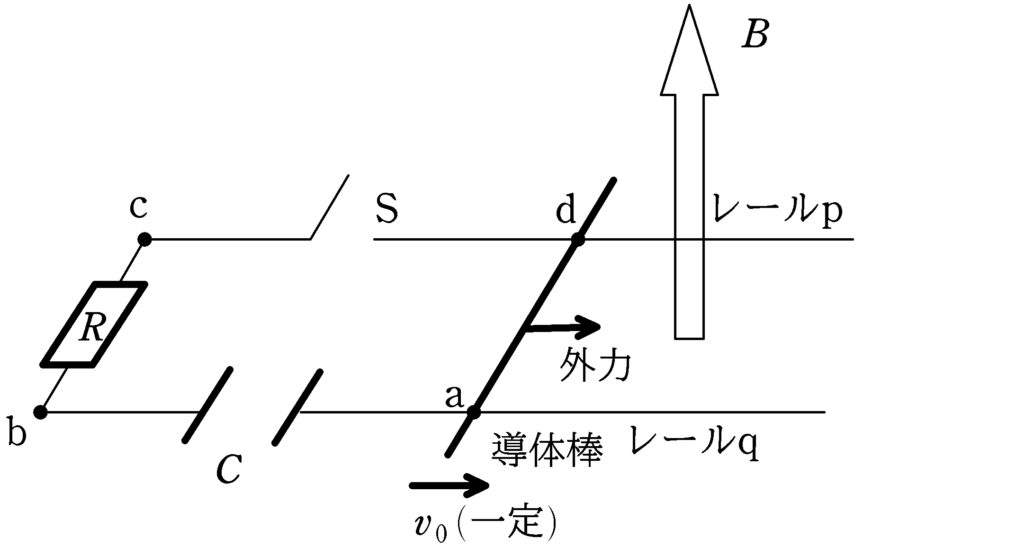
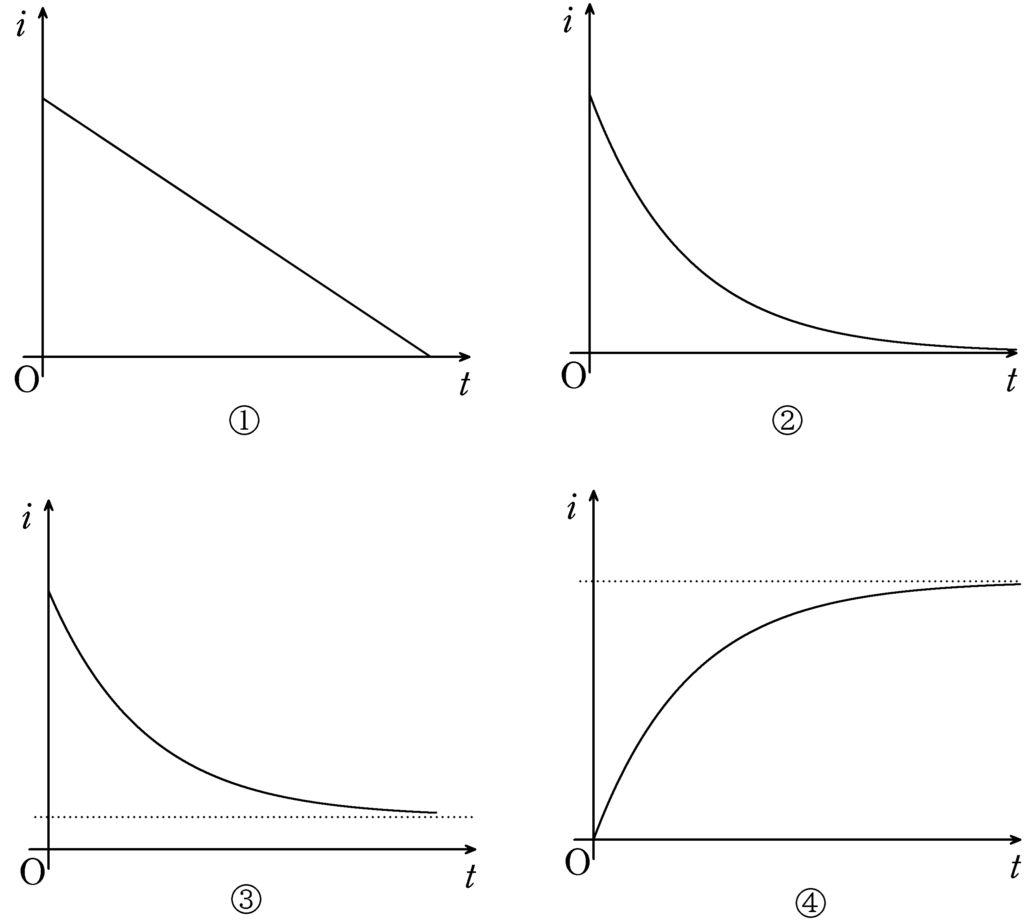
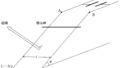
図のように水平面に平行な面に導体レールp , qが距離$l$を隔てて平行に固定されている．レールp , qに垂直に質量$m$の導体棒を置き，レールp , qに抵抗値$R$の抵抗と電気容量$C$の帯電していないコンデンサー，スイッチSを接続した．スイッチははじめ開かれている．鉛直上向きに磁束密度$B$の一様な磁場をかけ，導体棒を図の右方向に速度$v_{0}\,(>0)$を保つように外力を加え，導体棒はつねに導体レールに垂直になるように動いている．時刻$0$において，スイッチSを閉じた後の回路に流れる電流の時間変化（電流を$i$，時刻を$t$とする．）として正しいものを次の中から選べ．ただし，電流は図のa→b→c→dを正の向きとする．

PHYさん

グラフの問題は「感覚的に選ぶ」のではなく，「式を立てて考察する」癖をつけましょう．

確認すべきことは，今までの導体棒の問題と一緒です．

今回は，導体棒が起電力一定の直流電池ということを見抜けば，計算せずともグラフが予想できるはずです．

導体棒に生じる誘導起電力の公式（直線運動）

PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は，PQの長さを$l$，PQ方向に垂直な速さを$v_{\perp}$，導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば，

$V=v_{\perp}Bl$

導体棒の問題で立てて欲しい3つの式

回路の式（オームの法則，コンデンサーの基本式，電荷保存則など）
導体棒の運動に関する式（つり合いの式，運動方程式，運動量保存則など）
導体棒と回路の系全体のエネルギー収支の式

NEKO

今回は，導体棒に無理やり速度が$v_{0}$になるように外力が加えられているので，運動方程式を立てる意味はなさそうだね．

コンデンサーがあるので，

・キルヒホッフ則

・コンデンサーの式

・電流の定義式

を立てて解きましょう．

電流の定義式については，次の記事で$「+」$がつくのか，$「-」$がつくのかを説明しています．

電気容量の定義式

コンデンサーに蓄えられている電荷を$Q$，コンデンサー間の電圧を$V$とすれば，コンデンサーの電気容量$C$は

$C=\dfrac{Q}{V}$

実際は

$Q=CV$

として使うことが多い．

★　$t=0$における電流の大きさ

NEKO

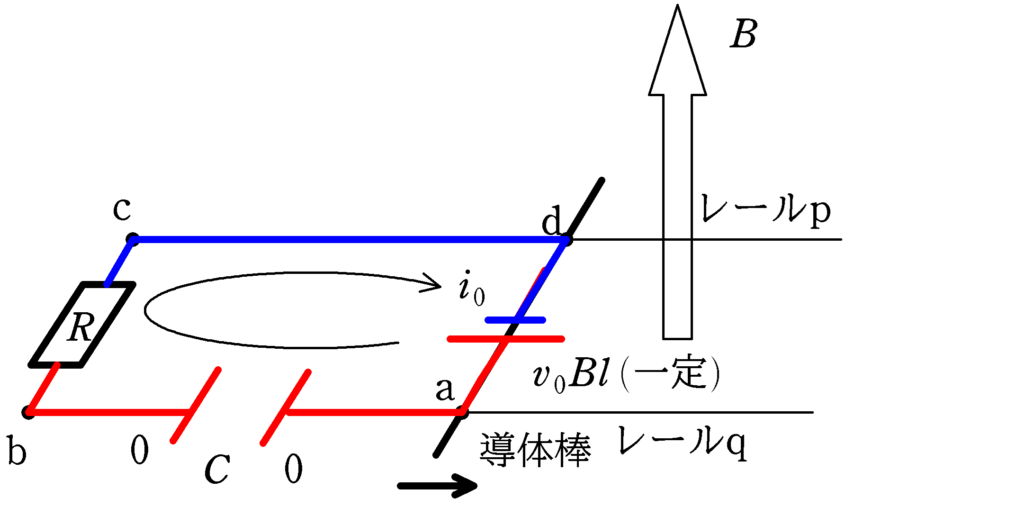
時刻0では，まだコンデンサーの電荷が0なので，コンデンサー間の電位差は0です．すると，キルヒホッフ則より，回路に流れる電流$i_{0}$は

$v_{0}Bl-Ri_{0}$

$i_{0}=\dfrac{v_{0}Bl}{R}$　$\cdots (\ast)$

となります．

電流が流れることで，図のコンデンサーの右側の電荷がプラスに帯電しそうだね．

★　時刻$t$における回路の式

NEKO

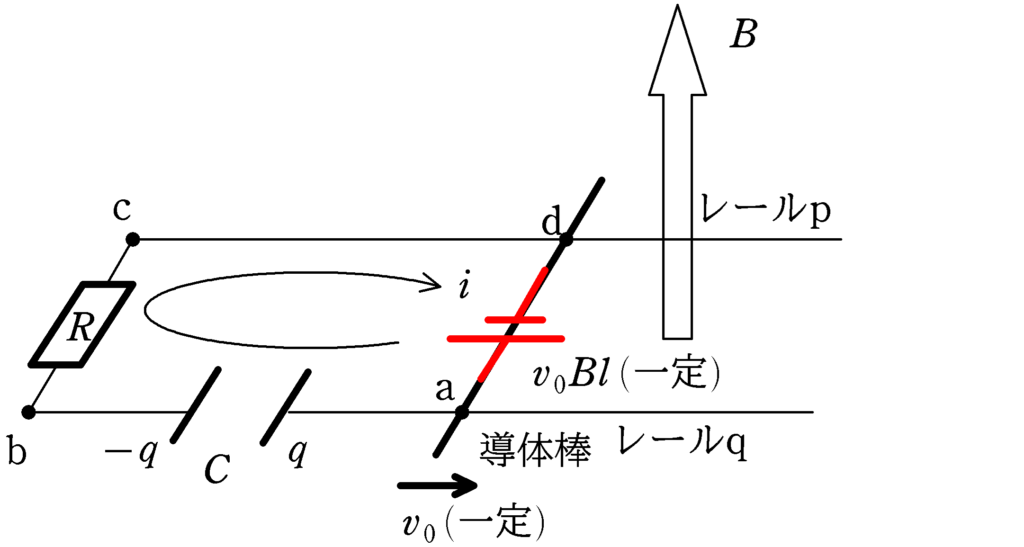
導体棒の起電力の大きさと向きは図の通りです．

時刻$t$において，コンデンサーに電荷$q$が帯電していて，回路に電流$i$が流れているとしましょう．コンデンサーにかかる電圧を$V$として，

・キルヒホッフ則

・コンデンサーの式

・電流の定義式

を立てます．

キルヒホッフ則より

$v_{0}Bl-V-Ri=0$　$\cdots (2\ast)$

コンデンサーの式より

$q=CV$　$\therefore V=\dfrac{q}{C}$　$\cdots (3\ast)$

$(3\ast)$を$(2\ast)$に代入して

$v_{0}Bl-\dfrac{q}{C}-Ri=0$

$\therefore q=CBlv_{0}-RCi$　$\cdots (4\ast)$

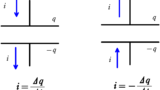
さらに，電流の定義式より($+q$に入りこむ向きが電流の正の向きになっている)

$i=\dfrac{\varDelta q}{\varDelta t}$　$\cdots (5\ast)$

$(4\ast)$を$(5\ast)$に代入して，$q$を消去すると

$\eqalign{i&=\dfrac{\varDelta }{\varDelta t}\left( CBlv_{0}-RCi \right)\\&=-RC\dfrac{\varDelta i}{\varDelta t}}$

NEKO

この式の形は運動方程式ではないけども「終端速度型」だね．

数学的には，次の記事のように解けるけど，

今までの運動方程式の形と同様に，

・$t=0$のときの$i-t$グラフの傾き

・$t\to\infty$では$i-t$グラフの傾きが0になる．すなわち，$\dfrac{\varDelta i}{\varDelta t}=0$になることから，$t\infty$での$i$の計算

をします．

$i= -RC\dfrac{\varDelta i}{\varDelta t} $　$\cdots (6\ast)$

について，$t=0$のとき，$(\ast)$より，回路に流れる電流$i_{0}$は

$i_{0}= \dfrac{v_{0}Bl}{R} $

なので，このときの$\dfrac{\varDelta I}{\varDelta t}$は$(6\ast)$より

$ \dfrac{v_{0}Bl}{R} = -RC\dfrac{\varDelta i}{\varDelta t} $

$\therefore \dfrac{\varDelta i}{\varDelta t}=-\dfrac{v_{0}Bl}{R^{2}C}\,(<0)$

NEKO

つまり，電流がだんだんと小さくなるんだね．

$t\to\infty$のとき，$\dfrac{\varDelta i}{\varDelta t}=0$であるから，このときの電流$i_{\infty}$は$(6\ast)$より

$i_{\infty}=0$

NEKO

つまり，最終的には電流が流れなくなるんだね．

導体棒の起電力が一定の直流電池であると考えれば，当たり前の結果だね．

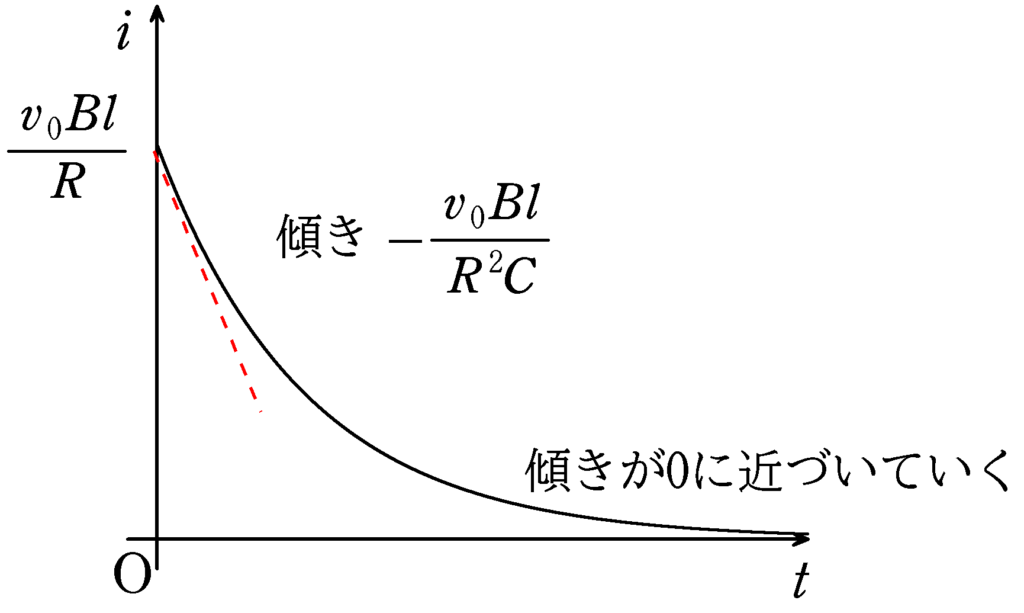
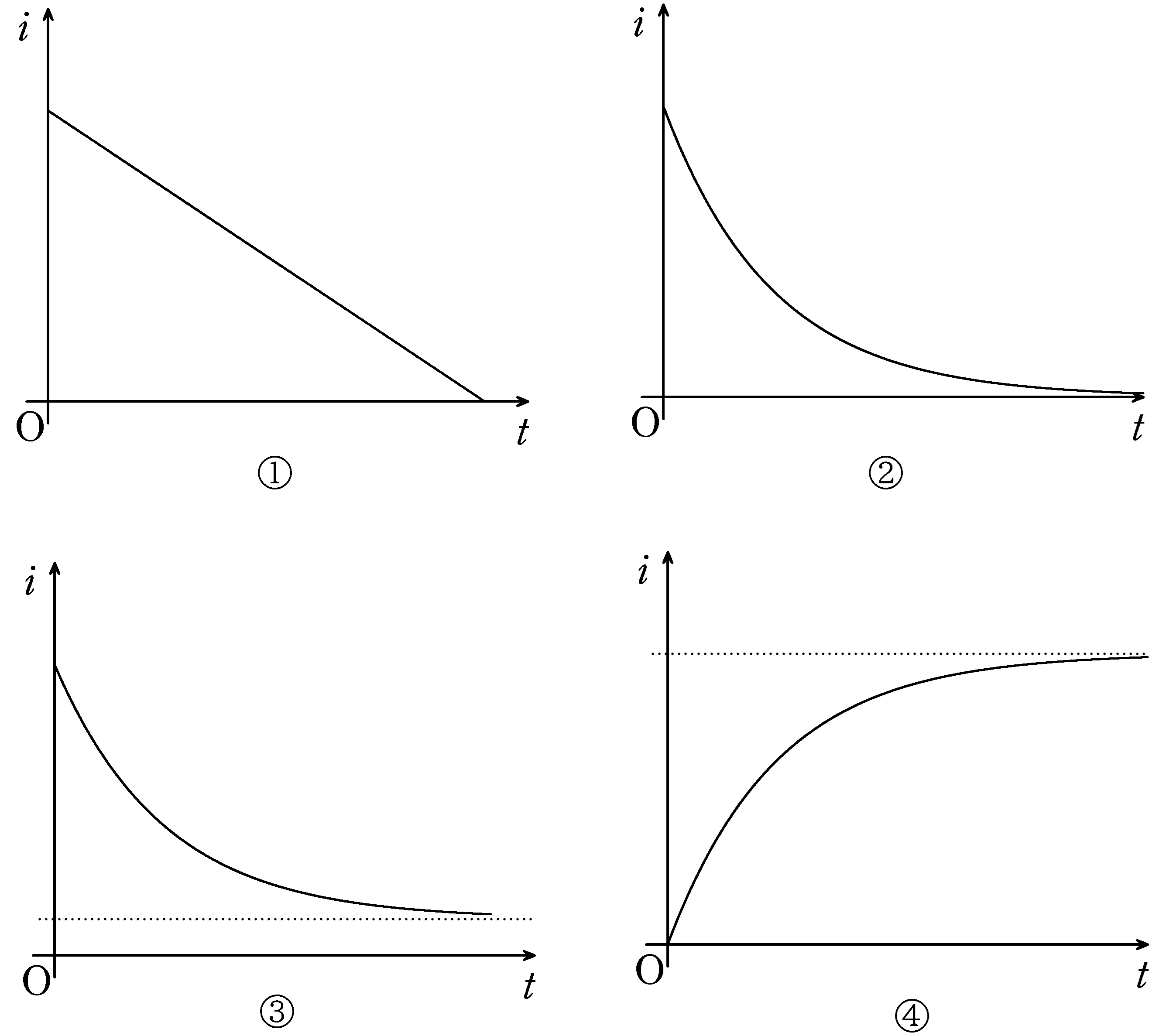
答えは，②（答）です．