
2022年の千葉大に出た電荷同士に静電気力がはたらく場合,速さが$0$になる打ち出し角度の問題について考えていきたいと思います.これは面積速度一定則を用いて説明ができます.
面積速度一定則はこちらで説明しています.
$\rm O$を中心として物体が運動しているときを考える.
物体の軌道面と平行な力が中心$\rm O$(または中心軸)を向くとき,面積速度$\dfrac{\Delta S}{\Delta t}$が一定となる.
面積速度は中心$\rm O$と物体を結ぶ線分が単位時間あたりに通過する面積である.
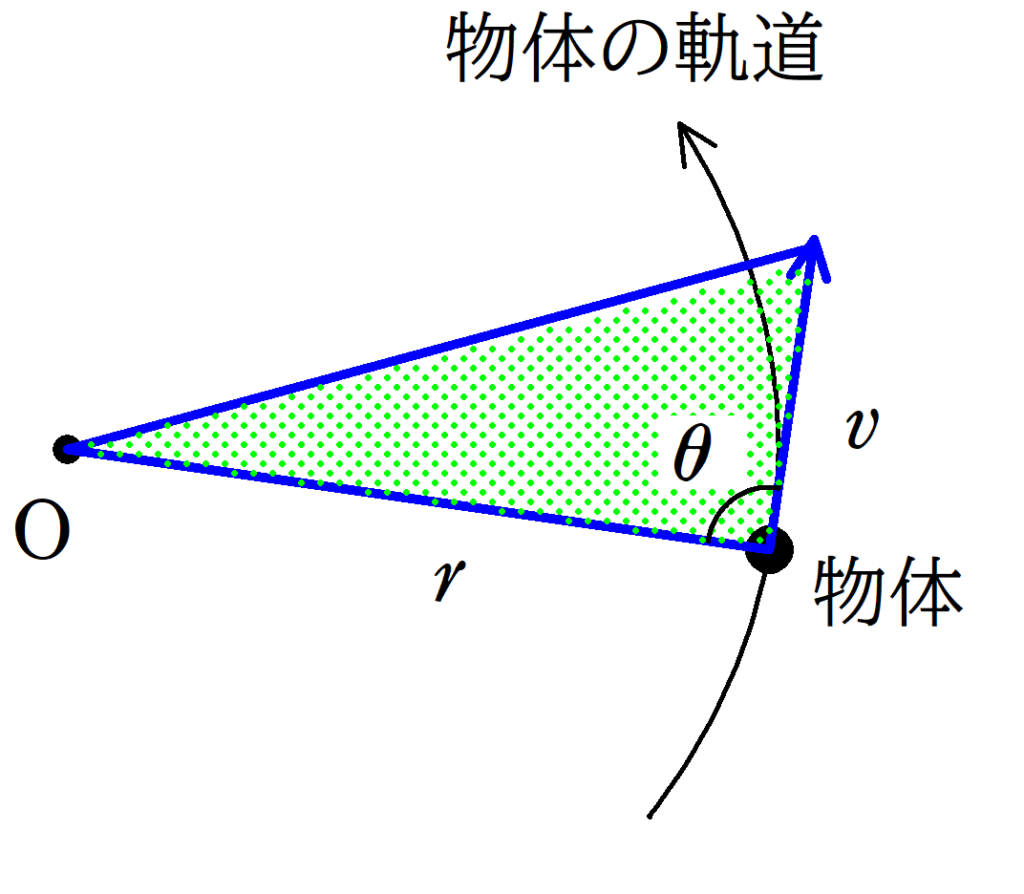
上図のように,$\rm O$と物体の距離が$r$,物体の速さを$v$,$\rm O$と物体を結ぶ線分と速度とのなす角を$\theta$とすると,面積速度は
$\dfrac{\Delta S}{\Delta t}=\dfrac{1}{2}rv\sin\theta$
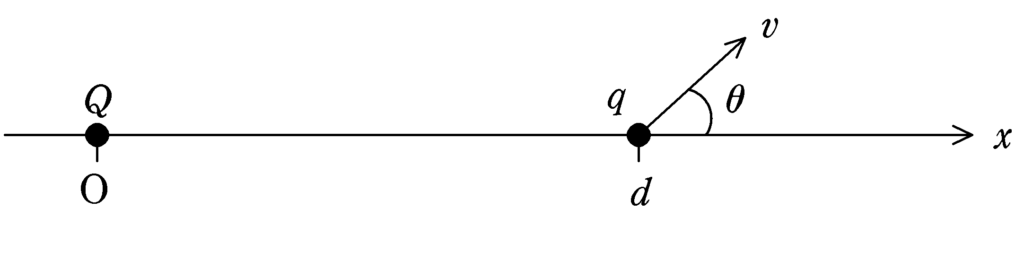
図のように,$x$軸上の原点Oに電荷$Q\,(>0)$の粒子と$x=d\,(>0)$の位置に電荷$q\,(>0)$の粒子が固定されている.電荷$q$の粒子の固定をはずし,$x$軸よりなす角$\theta\,(0^{\circ}\leqq \theta\leqq 180^{\circ})$の向きに大きさ$v\,(>0)$の初速を与えた.電荷$q$の粒子の速度の大きさが$0$になるような$\theta$を求めよ.

$Q$と$q$は同符号の電荷だから斥力がはたらくんだね.なので,$\theta=180^{\circ}$に打ち出すと,そのうち速度が$0$になるのはわかるんだけど,他の角度では$0$にならないのかな??

今回は,反発する向きに静電気力がはたらくので,面積速度一定則が成り立ちます.これを利用していきましょう.
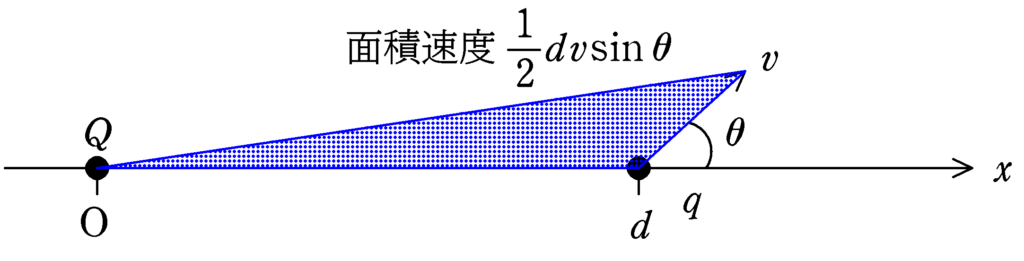

打ち出されたときの面積速度は上図の青色部分の面積だね.これは
$\dfrac{1}{2}dv\sin\theta$だね.

そうですね.途中で速度が$0$になるということは途中で面積速度も$0$になるということです.しかし,面積速度は一定なので,途中でいきなり面積速度が$0$になることはありません.
ということは,初速を与えた時点で面積速度が$0$になればいいということなります.

初速度があるのに,面積速度が一定になるなんていうことがあるの?
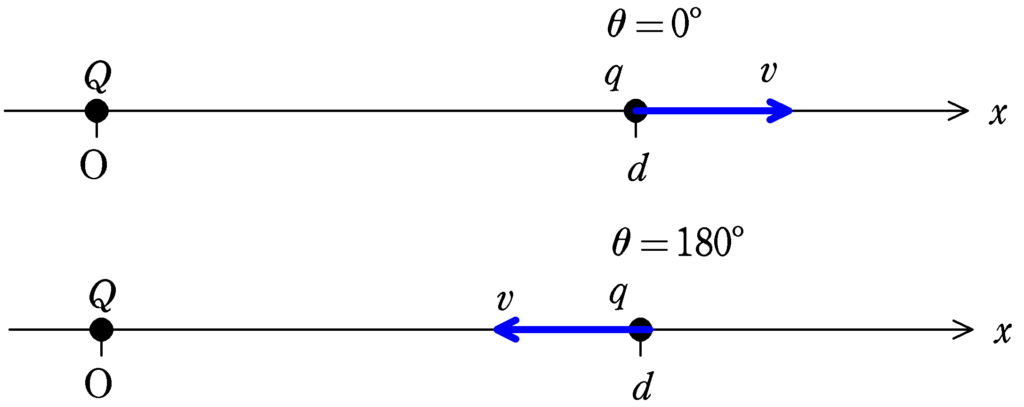

上のように$\theta=0^{\circ}$か$180^{\circ}$なら面積速度が$0$になります.

なるほど,だから$\theta=180^{\circ}$だと速さが$0$になる可能性があるんだ!
$\theta=0^{\circ}$のときは,常に進む方向と同じ方向に静電気力がはたらくから絶対に速さは$0$にならないんだね.

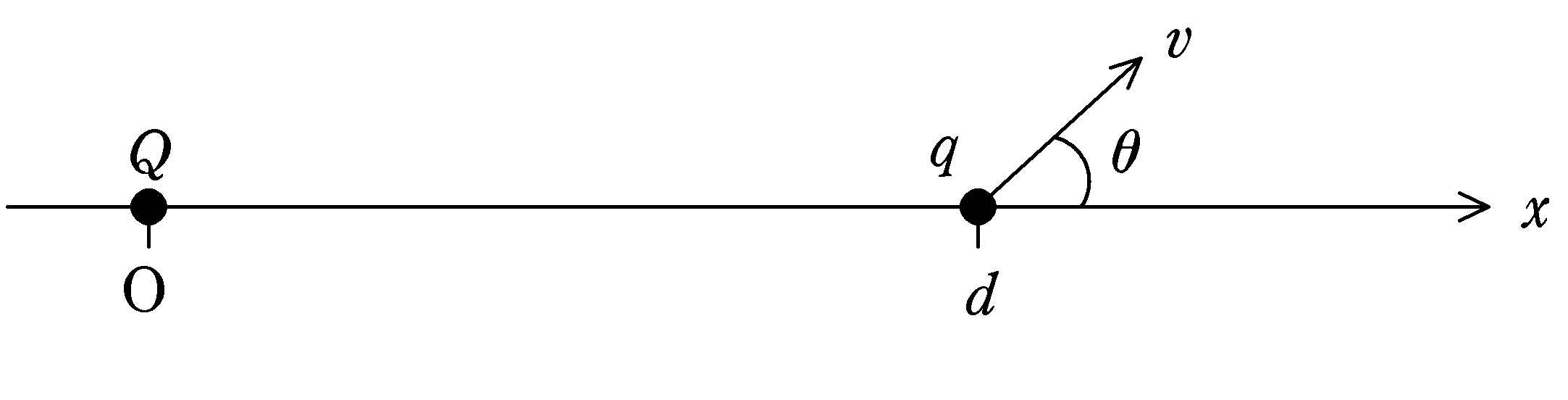

コメント