
前回の内容はこちらです.
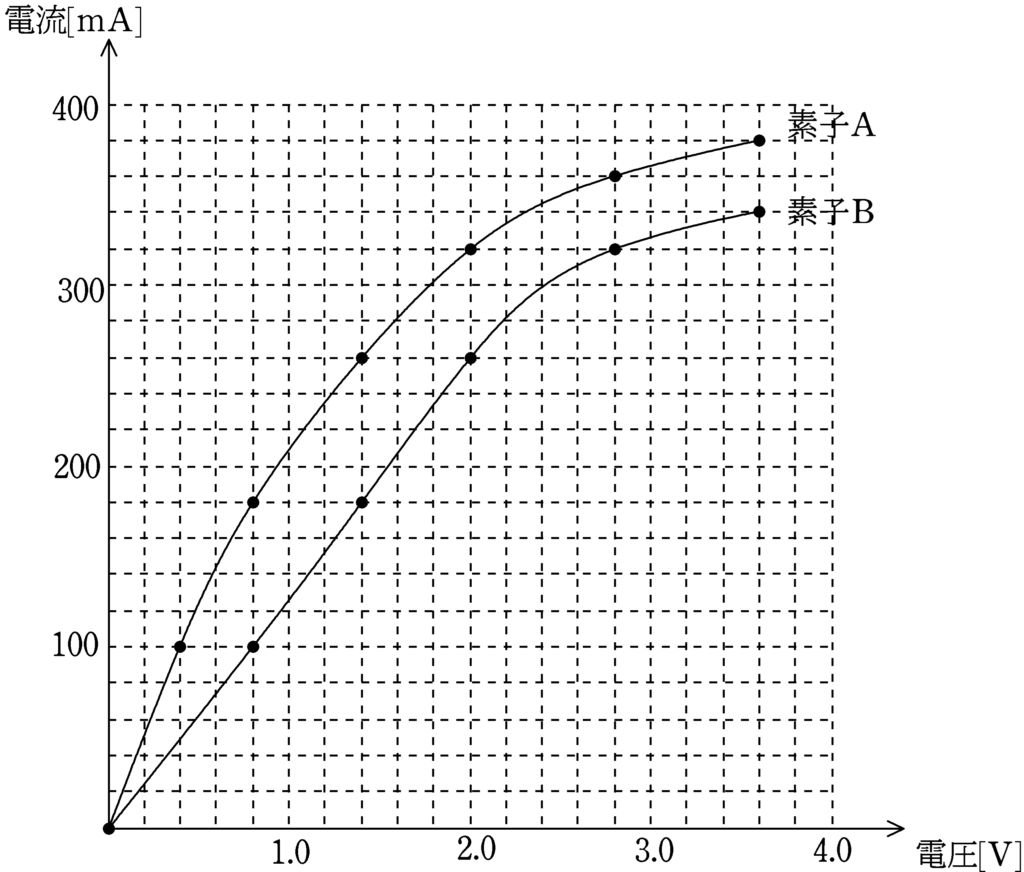
素子Aと素子Bに流れる電流$[\rm mA]$とかかる電圧$[\rm V]$の関係は上図の特性曲線で与えられている.このとき,次の問いに答えよ.
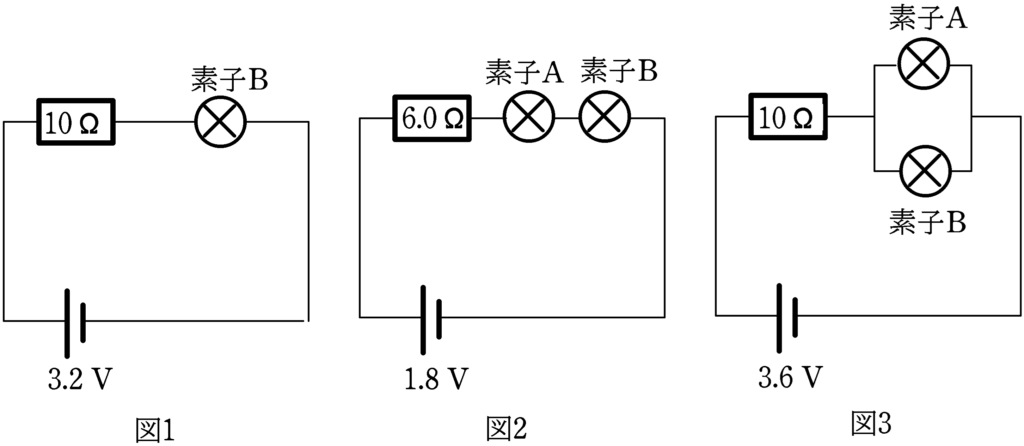
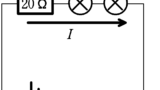
(1) 起電力$3.2\,\rm V$の内部抵抗の無視できる直流電池と$10\,\Omega$の抵抗,素子Bを図1のように導線でつなげたときにこの回路に流れる電流の大きさ$[\rm mA]$を求めよ.
(2) 起電力$1.8\,\rm V$の内部抵抗の無視できる直流電池と$6.0\,\Omega$の抵抗,素子A,素子Bを図2のように導線でつなげたときにこの回路に流れる電流の大きさ$[\rm mA]$を求めよ.
(3) 起電力$3.6\,\rm V$の内部抵抗の無視できる直流電池と$10\,\Omega$の抵抗,素子A,素子Bを図3のように導線でつなげたときにこの回路に流れる電流の大きさ$[\rm mA]$を求めよ.
- 特性のある素子に流れる電流とかかる電圧を設定する.
- キルヒホッフ則を立てる.
- 2.で得た回路の式を特性曲線のグラフに書き込み交点を求める.(特性の式が与えられていたら共通解を求める.)
<解答>
(1)
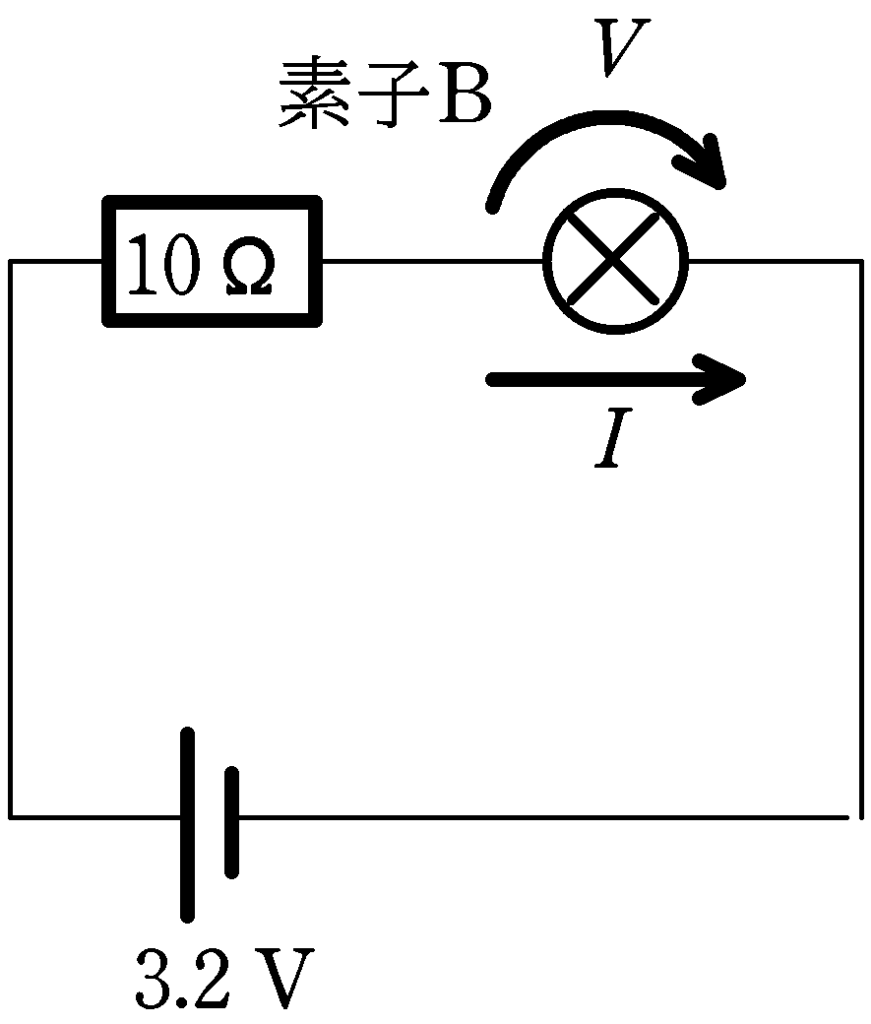

これは今までと同じだね.素子Bに流れる電流を$I\,[\rm mA]=\dfrac{I}{1000}\,[\rm A]$(※前回解説したように特性のグラフの縦軸が$[\rm mA]$になっているため),かかる電圧を$V$としてキルヒホッフの法則を立ててみよう.
★ キルヒホッフ則
$3.2-10\times \dfrac{I}{1000}-V=0$
$\therefore\,\, I=-100V+320 [\rm mA]$
これを特性のグラフに書き込んで交点を求めると
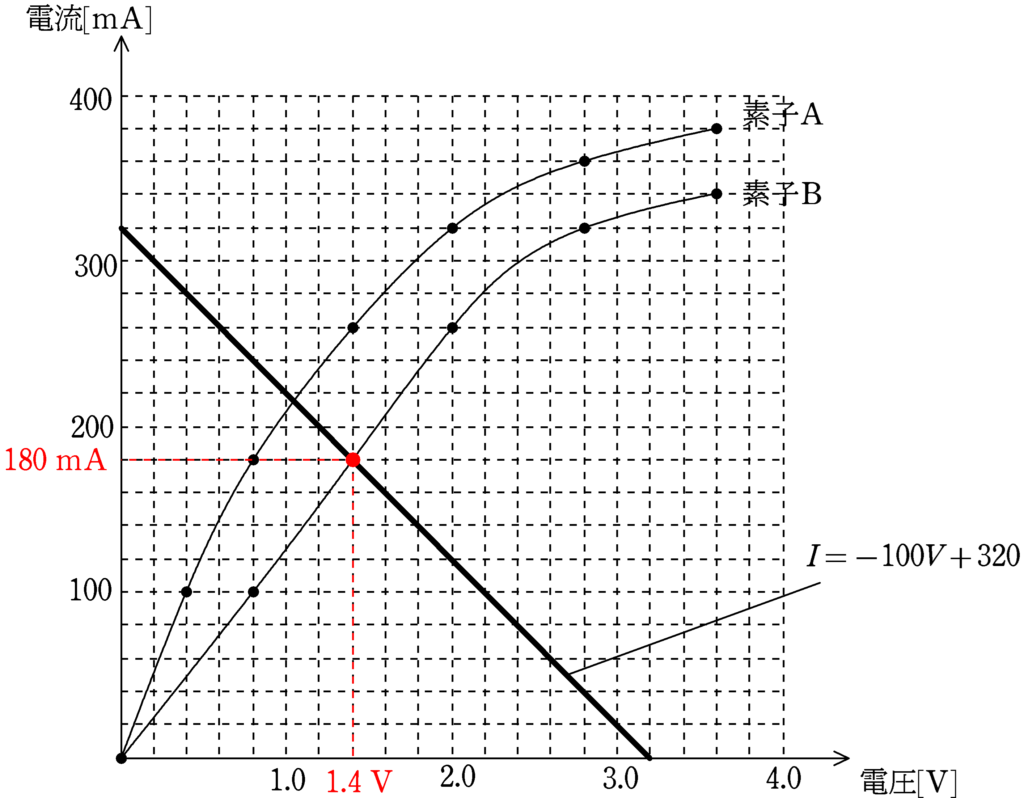
したがって,流れる電流は$180\,\rm mA$(答)
(2)

次は別々の特性をもつ回路だから,前みたくどちらも同じ電流と同じ電圧じゃまずいよね?

そうですね.キルヒホッフ第1法則より,AとBに流れる電流は同じなので,とりあえず,$I\,[\rm mA]$とおきましょう.
特性曲線によれば,同じ電流が流れても電圧が違うようなので,Aにかかる電圧を$V_{\rm A}\,[\rm V]$,Bにかかる電圧を$V_{\rm B}\,[\rm V]$として,キルヒホッフ則を立ててみましょう.
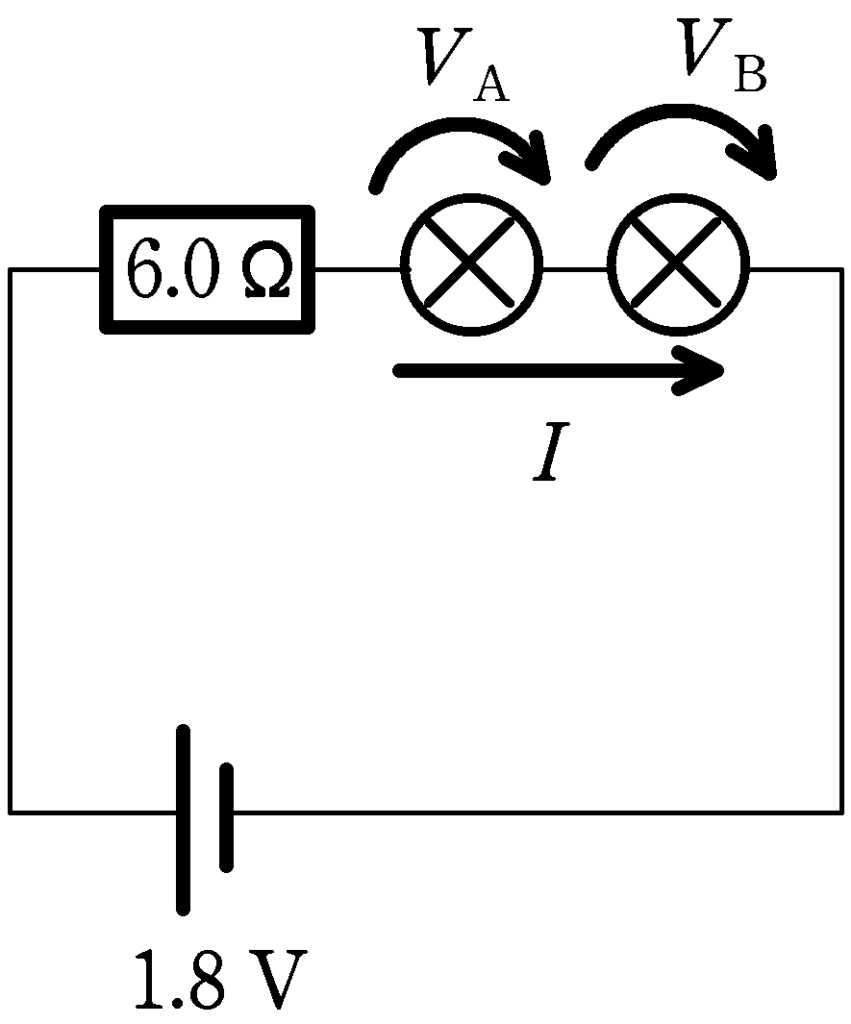
★ キルヒホッフ則
$1.8-6.0\times \dfrac{I}{1000}-V_{\rm A}-V_{\rm B}=0$

でもこれでは,グラフがかけないよ.$V_{\rm A}$と$V_{\rm B}$の関係もわからないんだし.

では,新たに同じ電流$I\,[\rm mA]$が流れたときに素子A,B全体にかかる電圧$V_{\rm A}+V_{\rm B}\,[\rm V]$の特性曲線のグラフをつくってみましょう.
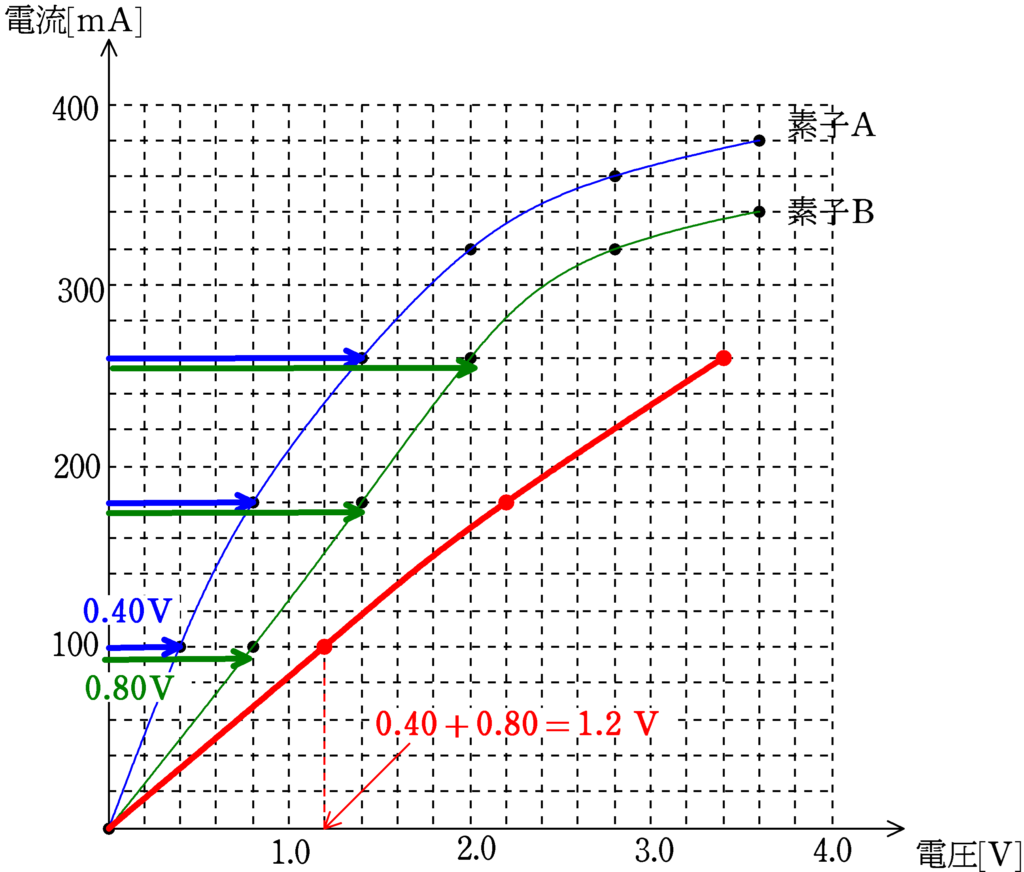

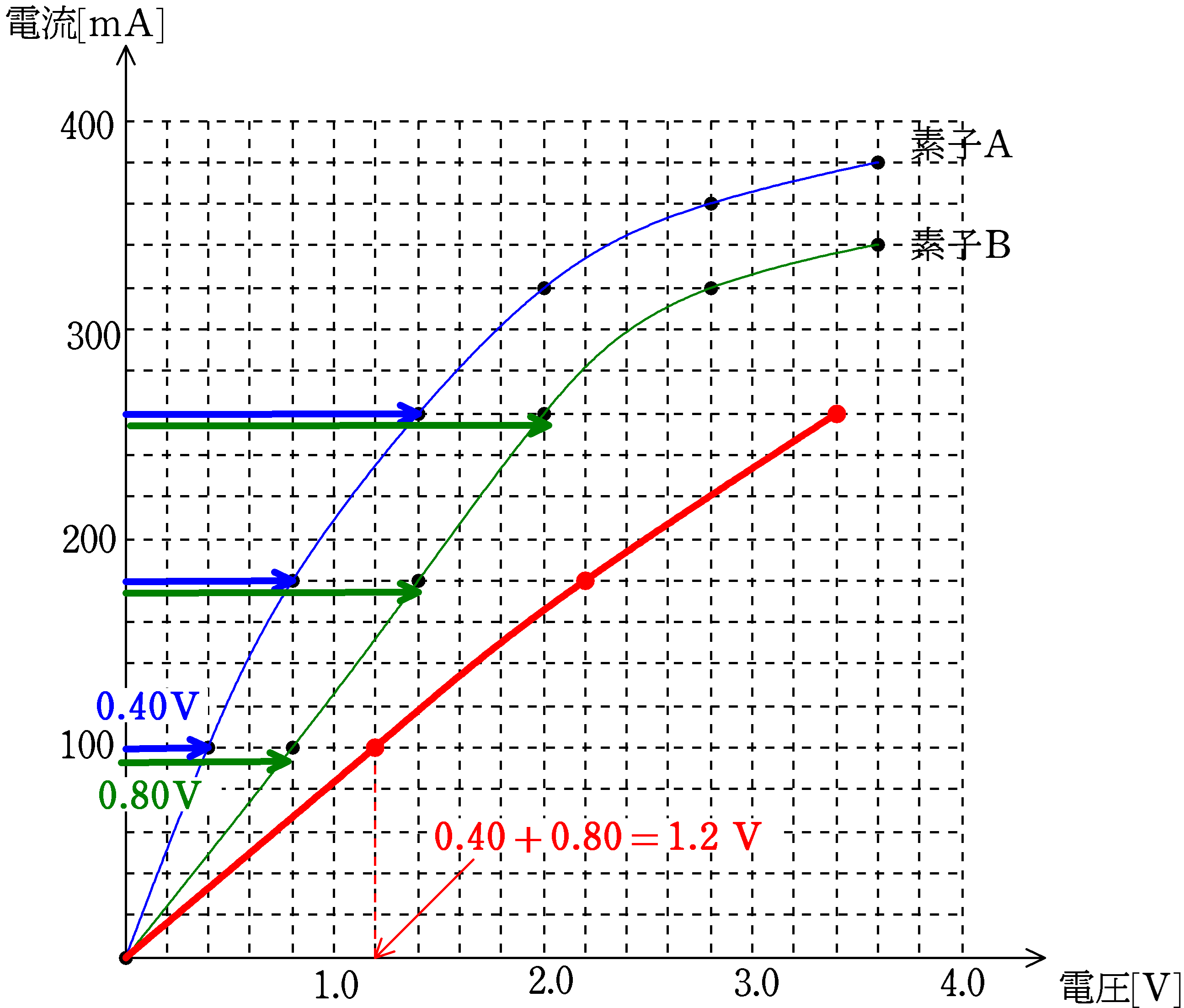
たとえば,回路に$100\,\rm mA$の電流が流れるときに素子Aにかかる電圧は$0.40\,\rm V$,素子Bにかかる電圧は$0.80\,\rm V$なので,素子A,B全体にかかる電圧は
$0.40+0.80=1.2\,\rm V$
です.また,回路に$180\,\rm mA$の電流が流れたときに素子Aにかかる電圧は$0.80\,\rm V$,素子Bにかかる電圧は$1.4\,\rm V$なので,素子A,B全体にかかる電圧は
$0.80+1.4=2.2\,\rm V$
となります.
このようにして,特性曲線を合成していきます.
実際,すべての点について電圧を足し合わせるのは大変なので,特に,回路の式との交点付近だけでも慎重に計算しておくようにしましょう.

では,あらためて,AとBを合成した素子にかかる電圧を$V\,[\rm V]$,流れる電流を$I\,[\rm mA]$として,キルヒホッフ則を立ててみましょう.
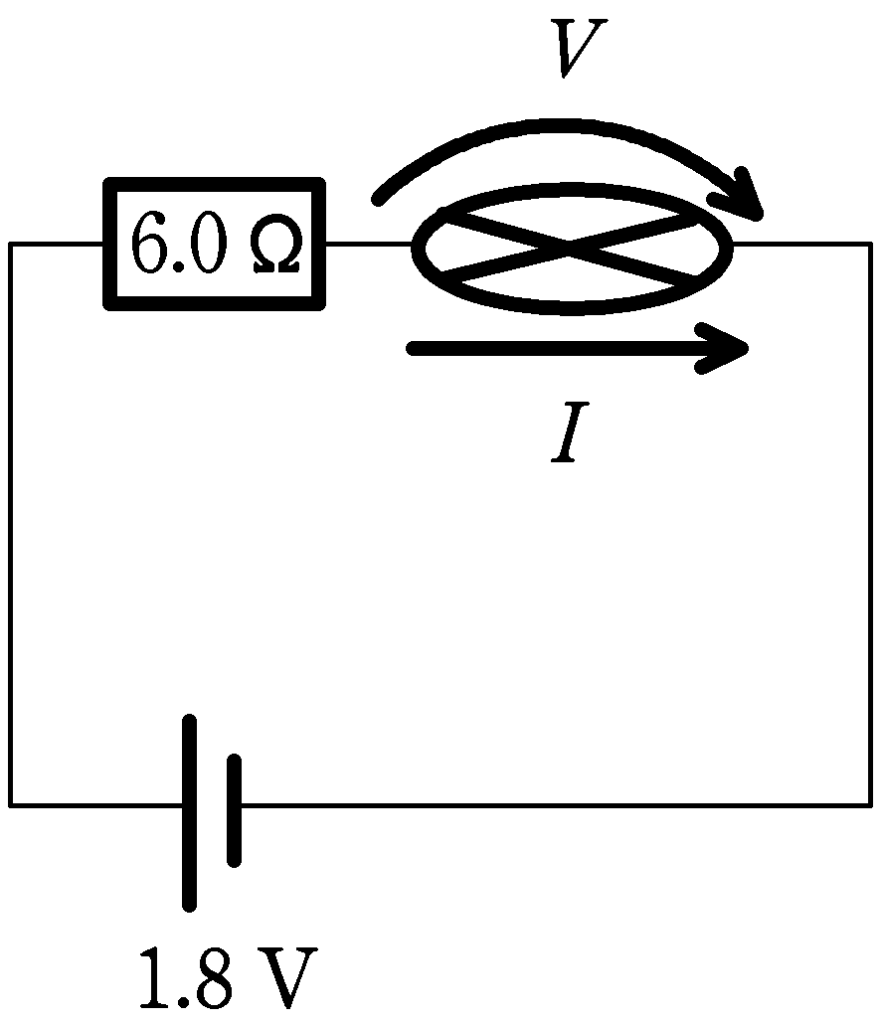
★ あらためて,キルヒホッフ則
$1.8-6.0\times \dfrac{I}{1000}-V=0$
$\therefore\,\, I=-\dfrac{500}{3}V+300 \,[\rm mA]$

この直線と合成した曲線の交点を求めてみましょう.
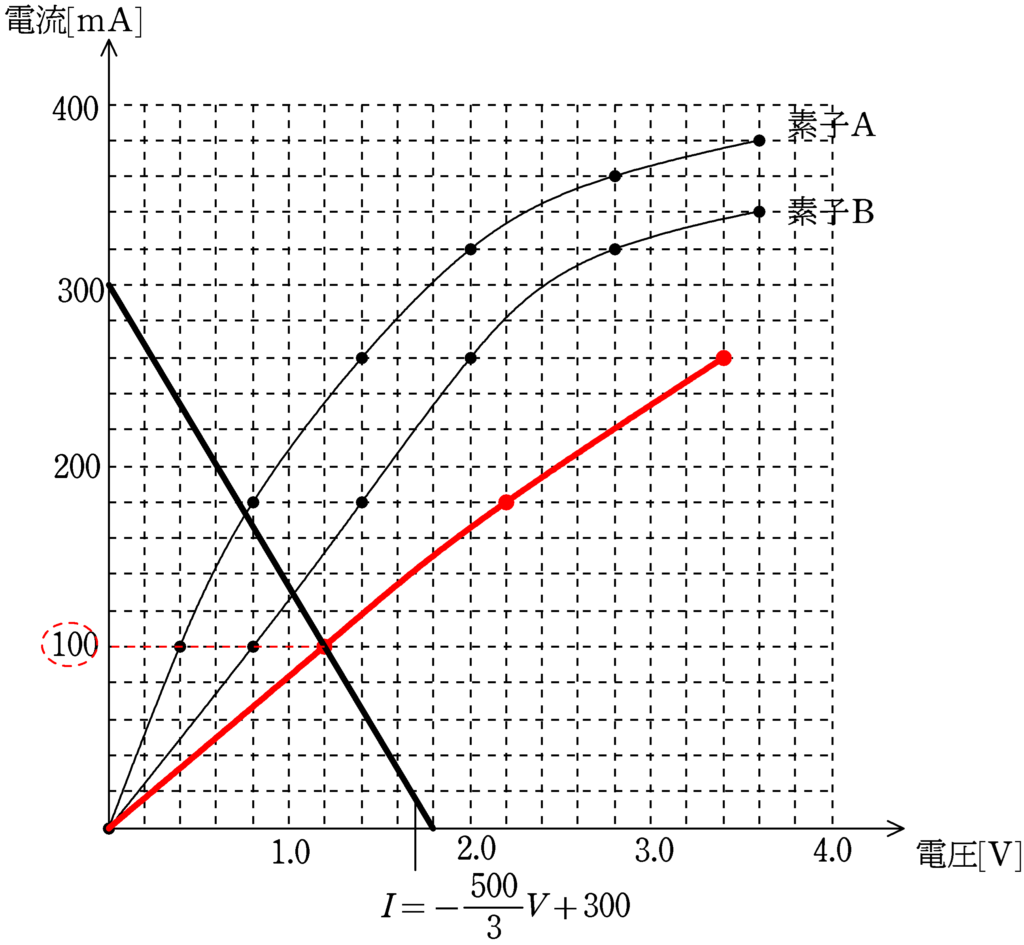

答えは,$100\,\rm mA$(答)です.
(3)
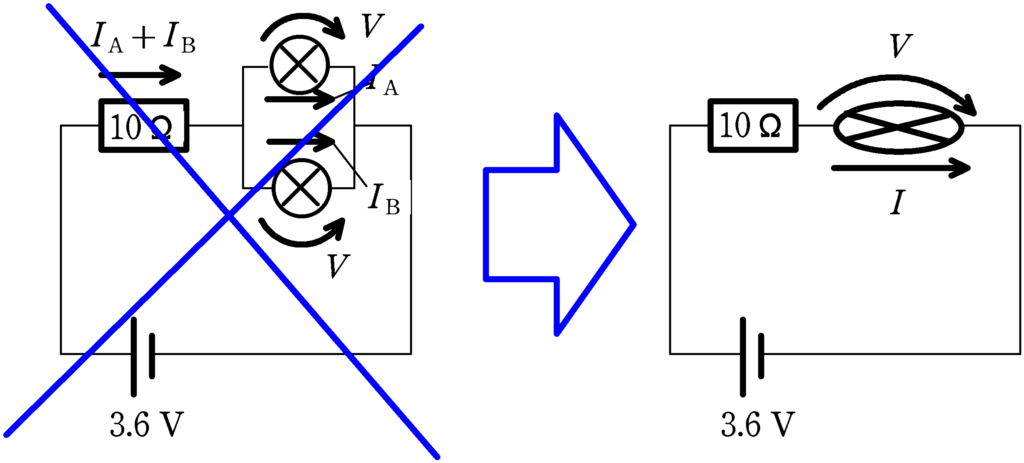

今度は素子A,Bにかかる電圧は同じです.同じ電圧に対して電流を足し合わせていきましょう.
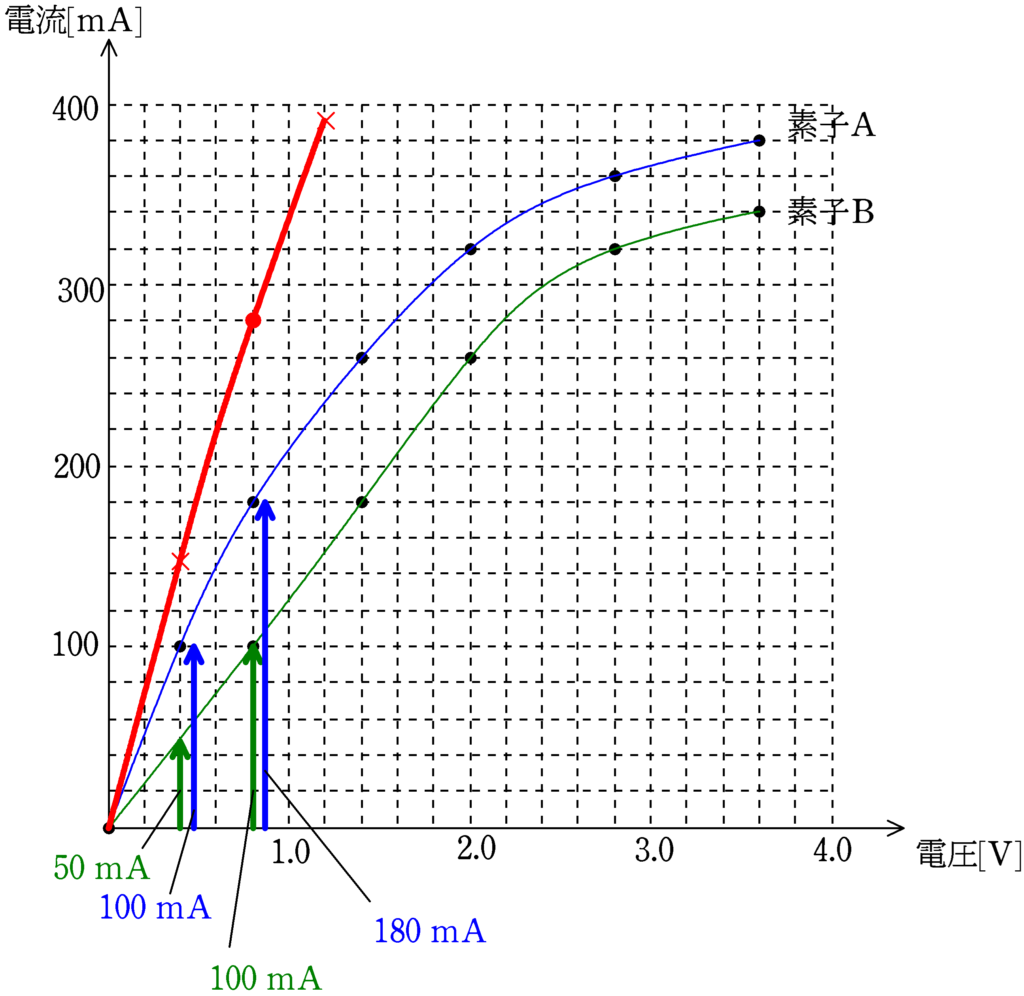

たとえば,素子A,Bにかかる電圧が$0.40\,\rm V$のとき,素子Aに流れる電流は$100\rm mA$,素子Bに流れる電流は約$50\,\rm mA$だから,合わせて約$150\,\rm mA$の電流が流れるんだね.
このようにして合成したものが赤の曲線です.
合成した素子に流れる電流を$I\,[\rm mA]$,かかる電圧を$V\,[\rm V]$としてキルヒホッフ則を立てると
★ キルヒホッフ則
$3.6-10\times\dfrac{I}{1000}-V=0$
$\therefore\,\, I=-100V+360 \,[\rm mA]$

この式と合成した曲線の交点を求めます.
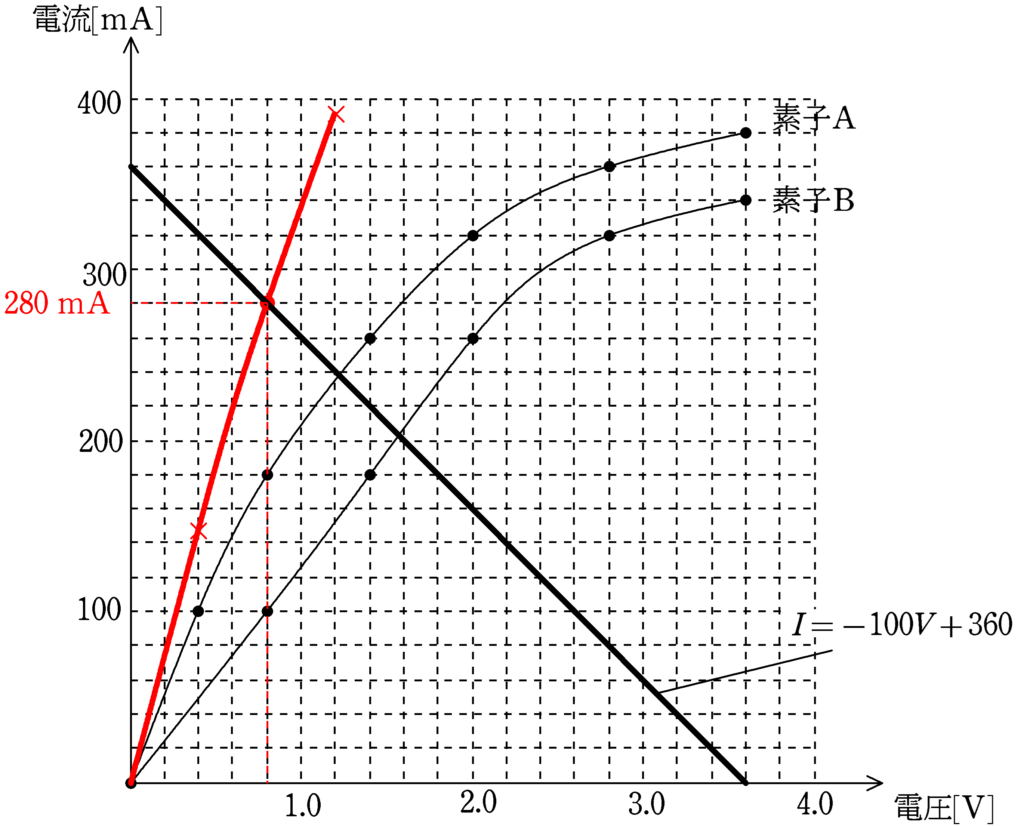

答えは,$280\,\rm mA$(答)です.


コメント