twitterの問題29の解答 | Physicmath（フィジクマス）

崩壊定数を求める問題。 pic.twitter.com/OKlapoPQL1
— フィジクマス (@physicmath2) November 9, 2022

＜問題＞

<解答>

問題文で書かれていることを読み取って問題を解く．

(7)　これは覚えておく．

半減期の式

時刻$t=0$における放射性元素の数を$N_{0}$とする．時刻$t$における放射性元素の数を$N(t)$とする．半減期（放射性元素の数が半分になるまでの時間）を$T$とすると，次の式が成り立つ．

$N(t)=N_{0}\left(\dfrac{1}{2}\right)^{\frac{t}{T}}$

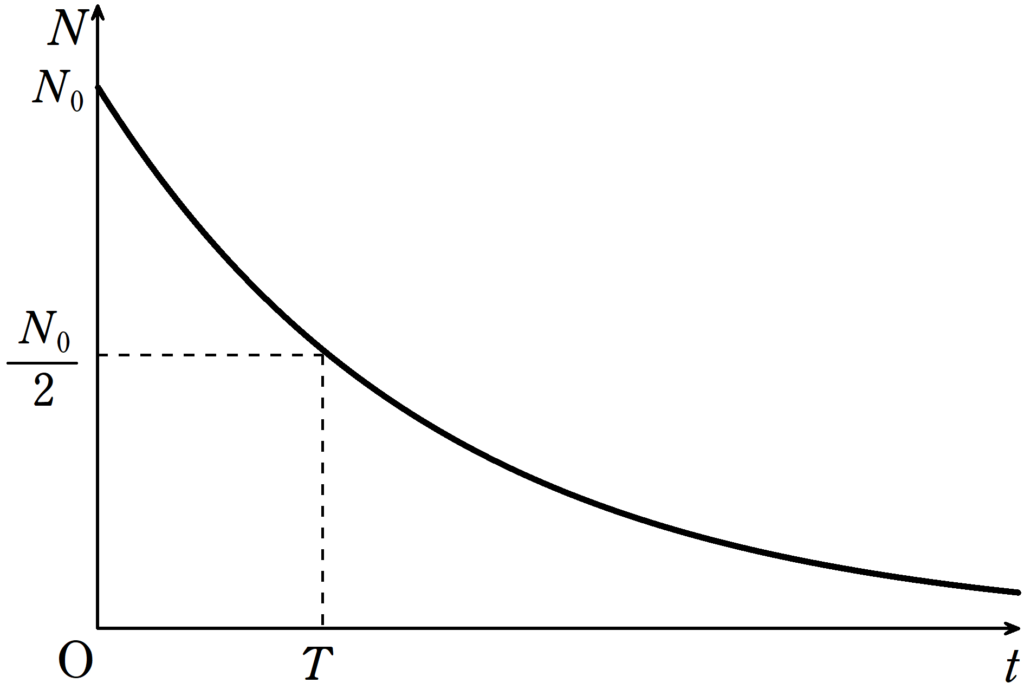
$N(t)=N_{0}\left(\dfrac{1}{2}\right)^{\frac{t}{T}}$(答)

(8)　この後は崩壊定数を求めることを目標としています．下の記事では崩壊定数を微分を使って計算しています．今回も微分の考えた方を使っていますが．しっかりと意味を考えていかないと解けない形になっています．

問題文より，$\varDelta N\,(<0)$は$N_{1}\,(>0)$と$\varDelta t\,(>0)$に比例することと，その比例係数が$k\,(>0)$であることから，左辺と右辺の符号を合わせるために「$-$」をつけて

$\varDelta N=-kN_{1}\varDelta t$(答)

(9)　まず，時刻$\varDelta t$での原子核数$N(\varDelta t)$を求めると，(8)の式を使って

$N(\varDelta t)=N_{0}-kN_{0}\varDelta t=N_{0}(1-k\varDelta t)$　$\cdots (\ast)$

$2\varDelta t$での原子核数$N(2\varDelta t)$は$(\ast)$を用いて

$\eqalign{N(2\varDelta t)&=N(\varDelta t)-kN(\varDelta t)\varDelta t\\&=N(\varDelta t)(1-k\varDelta t)\\&=N_{0}(1-k\varDelta t)(1-k\varDelta t)\\&=N_{0}(1-k\varDelta t)^{2}}$

$3\varDelta t$での原子核数$N(3\varDelta t)$は

$\eqalign{N(3\varDelta t)&=N(2\varDelta t)-kN(2\varDelta t)\varDelta t\\&=N(2\varDelta t)(1-k\varDelta t)\\&=N_{0}(1-k\varDelta t)^{2}(1-k\varDelta t)\\&=N_{0}(1-k\varDelta t)^{3}}$

このようにして，計算していくと，$L\varDelta t$での原子核数$N(L\varDelta t)$は

$N(L\varDelta t)=N_{0}(1-k\varDelta t)^{L}$

$\varDelta t=\dfrac{t}{L}$なので

$N(L\varDelta t)=N_{0}\left(1-\dfrac{k}{L}t\right)^{L}$　$\cdots (2\ast)$

問題文に書かれている自然対数の底の定義

$\displaystyle{e^{a}=\lim_{L\to \infty}\left(1+\dfrac{a}{L}\right)^{L}}$

を用いて

$\eqalign{\left(1-\dfrac{k}{L}t\right)^{L}&=\left(1+\dfrac{(-kt)}{L}\right)^{L}\\&=\left(1+\dfrac{(-kt)}{L}\right)^{L}\\&=e^{-kt}}$

より，$(2\ast)$は

$N(L\varDelta t)=N_{0}e^{-kt}$ (答)

(10) (7)より，$N(L\varDelta t)=N_{0}\left(\dfrac{1}{2}\right)^{\frac{t}{T}}=N_{0}2^{-\frac{t}{T}}$であるから，$N(L\varDelta t)=N_{0}e^{-kt}$ の右辺と比較して

$\cancel{N_{0}}2^{-\frac{t}{T}}=\cancel{N_{0}}e^{-kt}$