
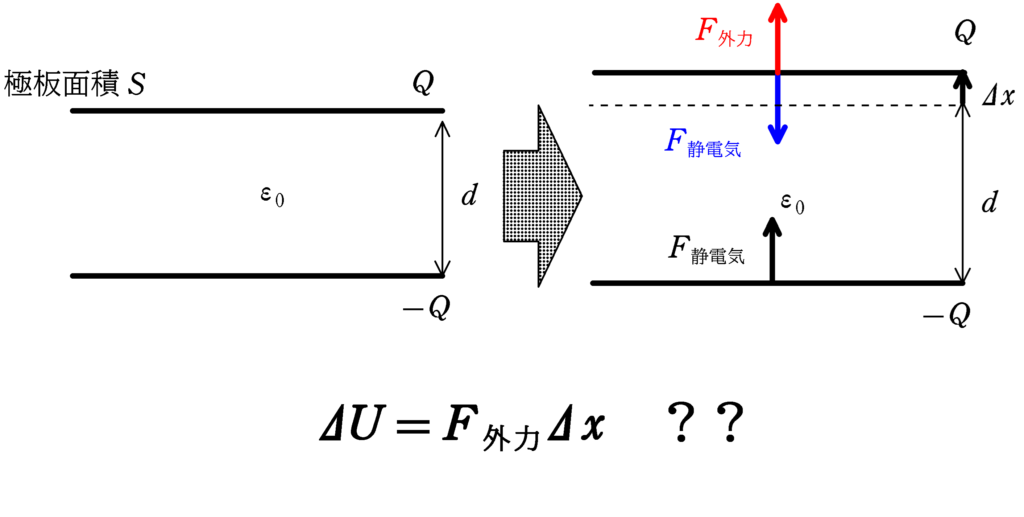
極板面積$S$の2枚の金属板に電荷$Q,-Q$が蓄えられている状態で下側極板を押さえておき,上側極板に外力を加えて極板間隔を$d\to d+\varDelta x$にゆっくり(つまり,つり合いを保ちながら)移動させる問題があるよね?
外力がする仕事を聞かることが多いと思うんだけど,このとき,コンデンサーの静電エネルギー変化を$\varDelta U$,外力がした仕事を$W_{外力}$として
$\varDelta U=W_{外力}$ $\cdots (\ast)$
の関係から計算するみたいなんだけど,極板には,静電気力もはたらいていて,負の仕事をしているはずだよね?
なんで静電気力がする仕事$W_{静電気}$を$(\ast)$に入れて
$\varDelta U=W_{外力}+W_{静電気}$
としないんだろう??

これは,
でも説明したように,
(静電気力のよる位置エネルギー変化)$=-$(静電気力がする仕事)

が成り立つからです.
同じように,力学では次の関係が成り立ちます.
(重力の位置エネルギー変化)$=-$(重力がした仕事)

重力は正の仕事をしてしまう分,ポテンシャル(潜在的なエネルギー)が失われてしまうという話だね.
たしか,一般的に次の関係が成り立つんだったね.
(位置エネルギーの変化)$=-$(保存力がする仕事)

はい.保存力,具体的には重力や弾性力,静電気力などの仕事をエネルギーとして考えるという話です.

え?もしかして,コンデンサーの静電エネルギーって,静電気力による位置エネルギーのことだったの??

そうです.
コンデンサーの場合,電位の基準点は無限遠ではなく,片一方(電荷が負の方)の電位を$0$として考えているはずです.実際,静電エネルギーの式の証明問題は入試でときどきみかけます.そのときに,$U=qV$の静電気力による位置エネルギー変化を考えているはずです.

つまり,次の式から
$\varDelta U=W_{外力}$
が説明できるんだね.
★ 極板に関して,運動エネルギー変化が$0$だから,
$0=W_{静電気}+W_{外力}$ $\cdots (2\ast)$
★ (位置エネルギーの変化)$=-$(保存力がする仕事)の関係より
$\varDelta U=-W_{静電気}$ $\cdots (3\ast)$
★ $(2\ast),(3\ast)$より,$W_{静電気}$を消去して
$\varDelta U=W_{外力}$

ちなみに,電池をつないで,コンデンサーの極板に力を加えゆっくりと動かしたときのエネルギーの関係は次のでいいのかな?
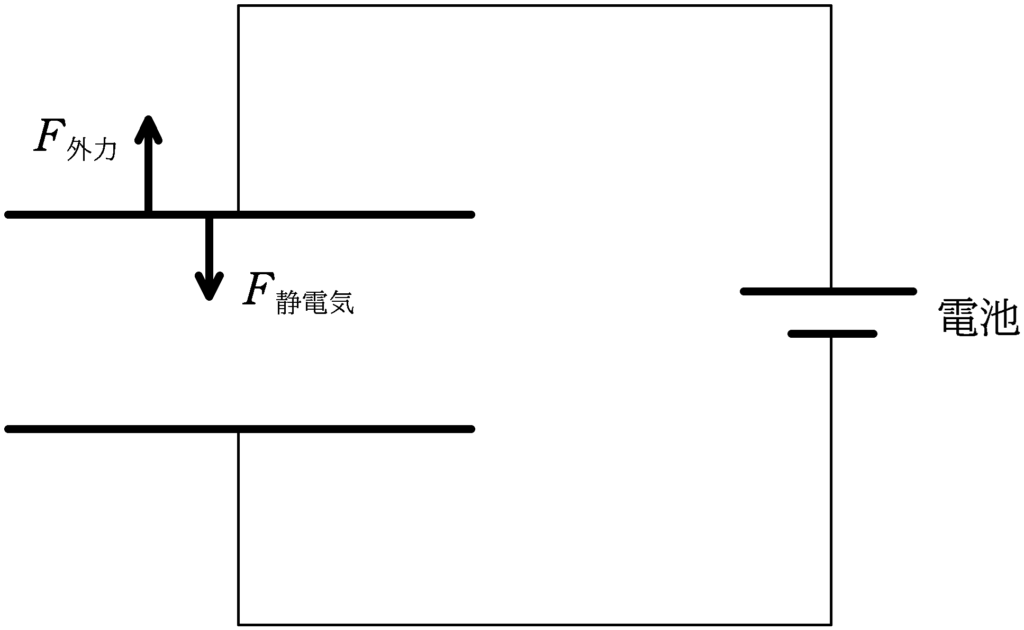
外力がした仕事を$W_{外力}$,静電気力がした仕事を$W_{静電気}$,電池がした仕事を$W_{電池}$,静電エネルギーの変化を$\varDelta U$とすると
$0=W_{静電気}+W_{外力}+W_{電池}$
$W_{静電気力}=-\varDelta U$
以上2式より
$\varDelta U=W_{外力}+W_{電池}$

はい.そういうことになります.
静電気力による位置エネルギーを入れて考えるので,静電気力がする仕事が消えるわけです.




コメント
いつもお世話になっています。助かってます。
電池をつないだ場合の運動エネルギーの変化と仕事の関係について質問があります。
外力がした仕事をW(外力)~の1つ下の式で”0=W(静電気)+W(外力) +W(電池)”とあるのですが、W (電池)がコンデンサーに対してどのような仕事をしているのか教えて欲しいです。
W(静電気)+W(外力) については上の極板が下のの極板や外からの受けている力についての仕事であるので納得できるのですが、W (電池)については、電池が極板に対して力が存在し仕事をしているのかよく分からないです。力学でこの関係式を用いるときは物体が受けている力についての仕事なので混乱しています。
電池は直接極板に仕事をするというよりも,電荷を移動させる仕事をしています.
電荷を移動させた結果,静電気力も変化し,静電気力が極板に仕事をするため,エネルギー保存則にいれる必要があります.
力学で無理やり考えると,万有引力がはたらいている2天体の片方に少しずつ物体を投げていくことで,質量が増すようなときに,物体を投げた分のエネルギー(仕事)を考慮する必要があります.この投げるときにした仕事が電池がした仕事です.
別件ですが,前に質問をいただいた「力学的エネルギー保存則」の説明は図が必要だったため,直接メールに送らせてもらっています.
細かいところがわからないようでしたら,メールでもかまわないので,質問を送ってください.
確認します。ありがとうございます!