
前回は,水平方向の板と物体の運動を扱いました!
今回は鉛直方向の運動です!↓前回の内容です.
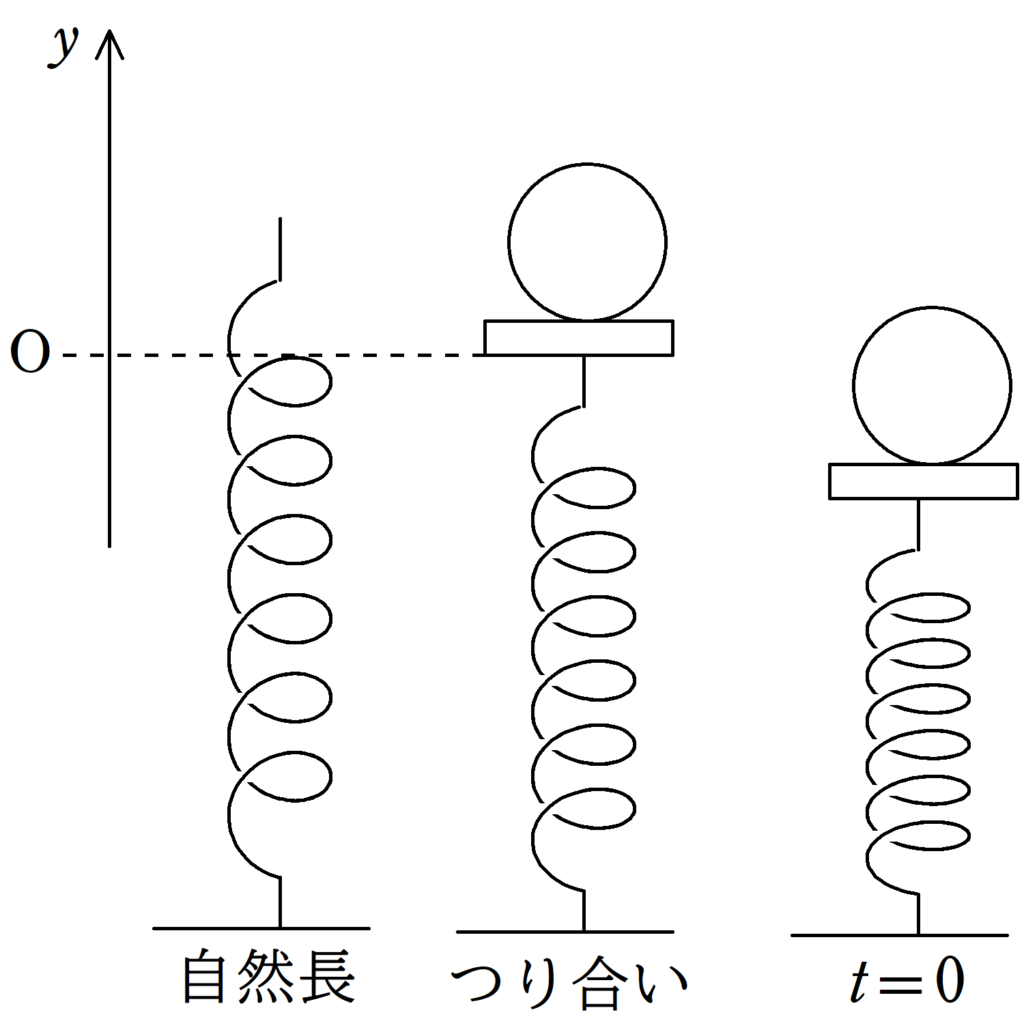
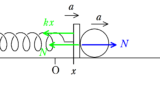
図のように,ばね定数$k$の軽いばねの一端を床に固定し,他端を質量$M$の板に固定した.板の上に質量$m$の物体ゆっくりとのせたところ自然長より$\varDelta y$だけ縮んでつり合った.このときの板の下端の位置を原点とし,鉛直上向きに$y$軸をとる.この状態からさらに,$y$軸の負の方向に$2\varDelta y$縮ませて時刻$t=0$で静かに手をはなすと板と物体は単振動をはじめ,時刻$t=t_{1}$のとき,物体は板から離れた.次の問いに答えよ.ただし,板の上面は常に水平であるとし,重力加速度の大きさを$g$とする.
(1) $\varDelta y$を$k$,$M$,$m$,$g$を用いて表せ.
(2) 時刻$0<t\leqq t_{1}$の間について,板の下端の位置が$y$であるときの板と物体の加速度を$y$軸の正の向きに$a$とする.このとき,板と物体それぞれの運動方程式を立てよ.ただし,板と物体の間にはたらく垂直抗力の大きさを$N$とする.
(3) (2)より,板の下端の位置が$y$のときの垂直抗力の大きさ$N$を$M$,$m$,$k$,$g$,$y$を用いて表せ.
(4) 時刻$0<t\leqq t_{1}$であるとき,板の下端の位置$y$を$t$,$M$,$m$,$k$,$g$を用いて表せ.
(5) 時刻$t_{1}$を$k$,$M$,$m$を用いて表せ.
(6) $0\leqq t \leqq t_{1}$である$t$のとき,板と物体の速度$v$を$t$,$M$,$m$,$k$,$g$を用いて表せ.
(7) 時刻$t=t_{1}$における板と物体の速さ$V$を$M$,$m$,$k$,$g$を用いて表せ.
<解答>
(1)
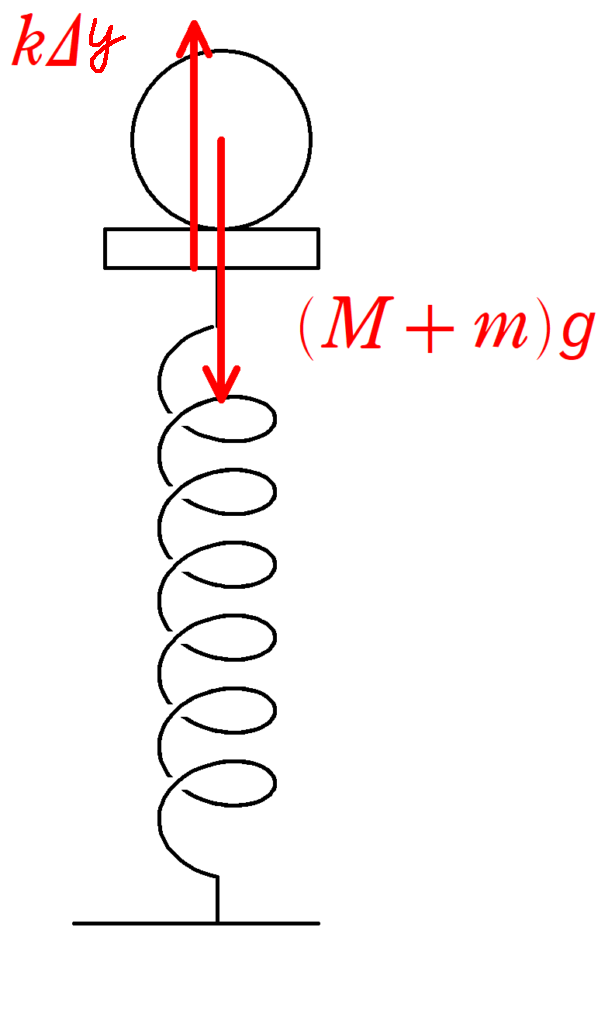
つりあっているときに物体系を板と物体とすれば,鉛直下向きに$(M+m)g$の重力と鉛直上向きに$k\varDelta y$の弾性力がかかります.つり合いの式より
$k\varDelta y =(M+m)g$ $\therefore$ $\varDelta y=\dfrac{M+m}{k}g$
(2)
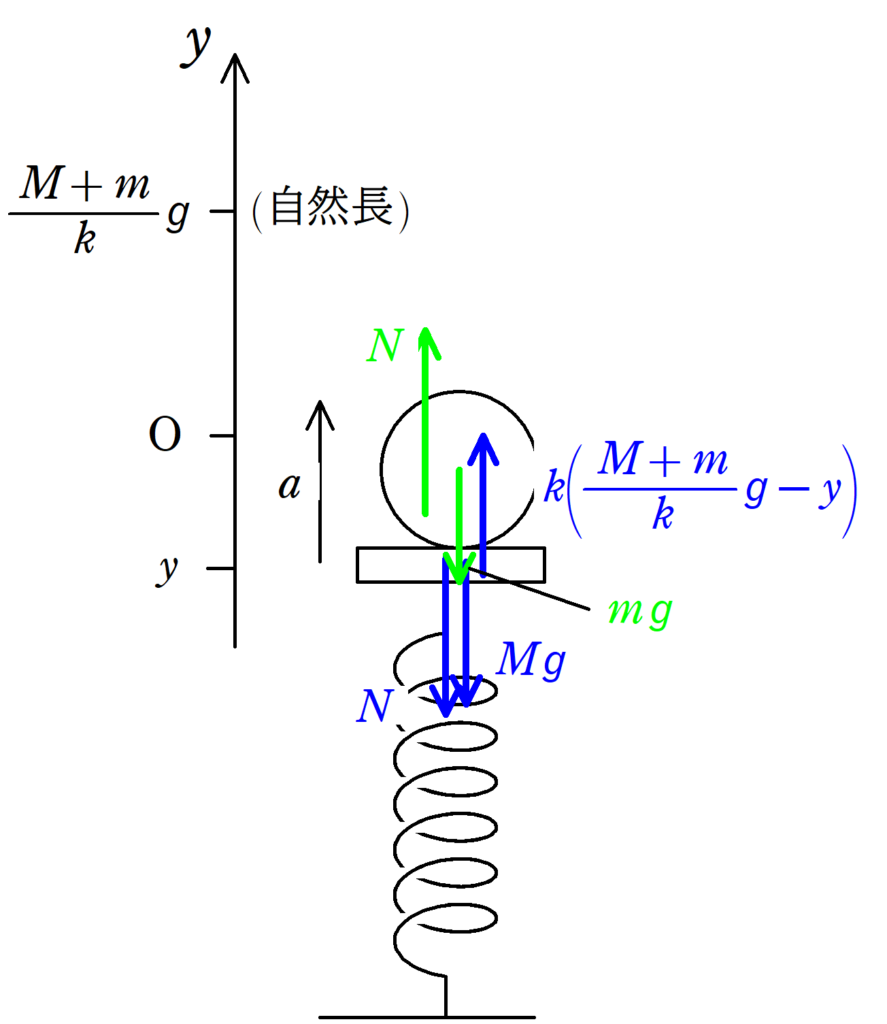
板には鉛直下向きに$Mg$,板と物体の間にはたらく垂直抗力$N$が鉛直下向きにはたらきます.また,上図では自然長より縮んでいるときのことを考えているので,鉛直上向きに弾性力がはたらきます.弾性力の大きさにも注意です.この問題では,つり合いの位置を原点にとっているため,弾性力の大きさは$k(-y)$ではありません.自然長からの距離が$\varDelta y-y$のため,弾性力の大きさは$k\left(\dfrac{M+m}{k}g-y\right)$となります.
一方,物体にははたらく力は重力と垂直抗力のみです.弾性力がはたらかないことに注意しましょう.
以上より運動方程式は
板:$Ma=k\left(\dfrac{M+m}{k}g-y\right)-Mg-N$ $\dots (\ast)$
物体:$ma=N-mg$ $\dots (2\ast)$
(3) $(\ast)$と$(2\ast)$を足して,$N$を消去すると
$(M+m)a=-ky$
$\therefore a=-\dfrac{k}{M+m}y$ $\dots (3\ast)$
これを$(2\ast)$に代入して,$N$を求めると
$\eqalign{N&=ma+mg\\&=m\cdot \left(-\dfrac{k}{M+m}y\right)+mg\\&=-\dfrac{mk}{M+m}y+mg}$
したがって,$N=$$-\dfrac{mk}{M+m}y+mg$
(4) $(3\ast)$より,振動の中心は$x_{0}=0$,角振動数は$\omega_{1}=\sqrt{\dfrac{k}{M+m}}$,周期は$T_{1}=2\pi \sqrt{\dfrac{M+m}{k}}$ということを確認できます.
また,$y=-2\varDelta y=-\dfrac{2(M+m)}{k}g$から速度0でスタートしているので,振幅は$\dfrac{2(M+m)}{k}g$です.
$-\cos$型であることに注意して
$y=$$-\dfrac{2(M+m)}{k}g\cos\left\{\sqrt{\dfrac{k}{M+m}}t\right\}$
(5) $N=0$のとき,(3)の$N=-\dfrac{mk}{M+m}y+mg$より
$0=-\dfrac{mk}{M+m}y+mg$
$\therefore y=\dfrac{M+m}{k}g$
すなわち自然長で離れます.
$y=\dfrac{M+m}{k}g$を$y=-\dfrac{2(M+m)}{k}g\cos\left\{\sqrt{\dfrac{k}{M+m}}t\right\}$に代入して一番小さい$t$を求めると
$\eqalign{\dfrac{M+m}{k}g&=-\dfrac{2(M+m)}{k}g\cos\left\{\sqrt{\dfrac{k}{M+m}}t\right\}\cr \cos\left\{\sqrt{\dfrac{k}{M+m}}t\right\}&=-\dfrac{1}{2}}$
$\therefore \sqrt{\dfrac{k}{M+m}}t=\dfrac{2\pi}{3}$
したがって,$t=$$\dfrac{2\pi}{3}\sqrt{\dfrac{M+m}{k}}$
(6) $y=-\dfrac{2(M+m)}{k}g\cos\left\{\sqrt{\dfrac{k}{M+m}}t\right\}$を$t$で微分すると速度$v$が計算できます.
$\eqalign{v&=\dfrac{dy}{dt}\\&=-\dfrac{2(M+m)}{k}g\cdot \left(\sqrt{\dfrac{k}{M+m}}t\right)^{\prime}\cdot \left(-\sin\left\{\sqrt{\dfrac{k}{M+m}}t\right\}\right)\\&=\dfrac{2(M+m)}{k}g\sqrt{\dfrac{k}{M+m}}\sin\left\{\sqrt{\dfrac{k}{M+m}}t\right\}\\&=2g\sqrt{\dfrac{M+m}{k}}\sin\left\{\sqrt{\dfrac{k}{M+m}}t\right\}}$
したがって,$v=$$2g\sqrt{\dfrac{M+m}{k}}\sin\left\{\sqrt{\dfrac{k}{M+m}}t\right\}$
(7) (6)の結果に,(5)の$t=\dfrac{2\pi}{3}\sqrt{\dfrac{M+m}{k}}$を代入して
$\eqalign{V&=2g\sqrt{\dfrac{M+m}{k}}\sin\left\{\sqrt{\dfrac{k}{M+m}}\cdot \dfrac{2\pi}{3}\sqrt{\dfrac{M+m}{k}}\right\}\\&=g\sqrt{\dfrac{3(M+m)}{k}}}$
したがって,$V=$$g\sqrt{\dfrac{3(M+m)}{k}}$

終わったー.速度を計算するの少し面倒だね・・・

実は,速度はエネルギー保存則でも計算できます.次回はエネルギー保存則の立式の練習です.
次回の内容はこちら




コメント
[…] [標準]単振動の演習問題④ 板と物体の運動2NEKO前回は,水平方向の板と物… […]
[…] [標準]単振動の演習問題④ 板と物体の運動2NEKO前回は,水平方向の板と物… 単振動 演習問題(標準) 高校物理 シェアする Twitter Facebook はてブ Pocket LINE コピー physicmathをフォローする physicmath Physicmath(フィジクマス) […]
[…] [標準]単振動の演習問題④ 板と物体の運動2NEKO前回は,水平方向の板と物… […]