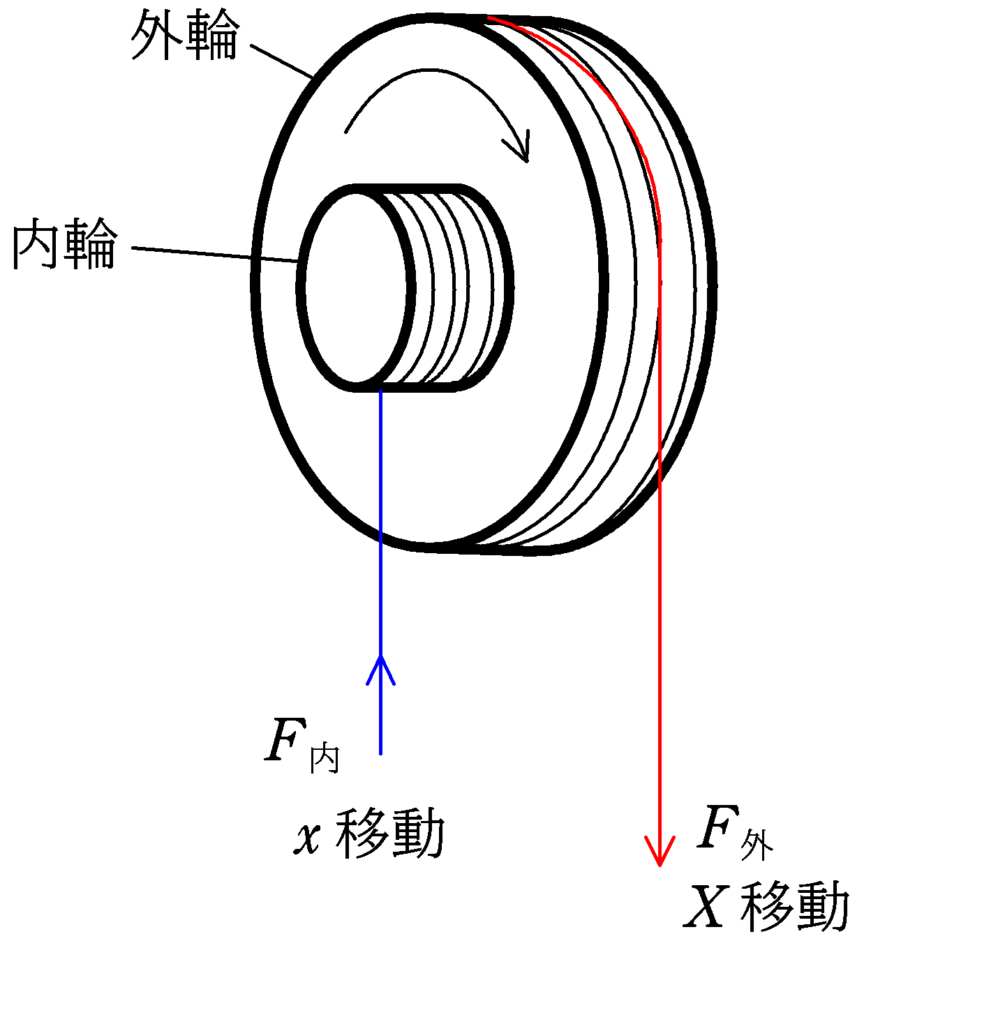

外輪の半径が$R$で内輪の半径が$r$の定滑車(十分軽いとし,摩擦や空気抵抗は無視)で,外輪側の張力と内輪側の張力の大きさの比や,外輪側にとりつけられた物体の加速度の大きさと内輪側にとりつけられた加速度の大きさの比が必要な問題をときどきみかけるんだけど,これは覚えておいた方がいいの?
外輪の半径が$R$で内輪の半径が$r$の定滑車について,外輪側の張力の大きさを$F_{外}$,内輪側の張力の大きさを$F_{内}$とすると,
$F_{外}:F_{内}=r:R$
また,外輪側の糸を長さ$X$だけ引っ張ったときに内輪側の糸が長さ$x$巻かれたときに
$X:x=R:r$
であるから,外輪側に取り付けられた物体の加速度の大きさ$a_{外}$と内輪側にとりつけられた物体の加速度の大きさを$a_{内}$として
$a_{外}:a_{内}=R:r$
が成り立つ.

覚えておいてもいいですが,次のように考えると丸暗記をしなくて済みます.
- 張力の大きさの比は「定滑車の力のモーメントのつり合いの式」で求める.
- 移動距離の比(加速度の比と一致)は「外輪と内輪の回転角は同じである」という式を立てて求める.
力のモーメントのつり合いの式で張力の大きさの比を求める.

滑車は質量が無視できるので,力のモーメントがつり合います.(高校範囲外ですが,滑車の質量が無視できない場合は外輪と内輪の半径が一致していても角加速度が生じている際は両端の張力は同じになりません.)
運動方程式$ma=F$の角度バージョンである回転の運動方程式
(慣性モーメント)$\times$(角加速度)$=$(力のモーメントの和)
で,質量が$0$とみなせるとき,「慣性モーメント」が$0$であり,「力のモーメントの和」が$0$になるからです.(高校範囲外)
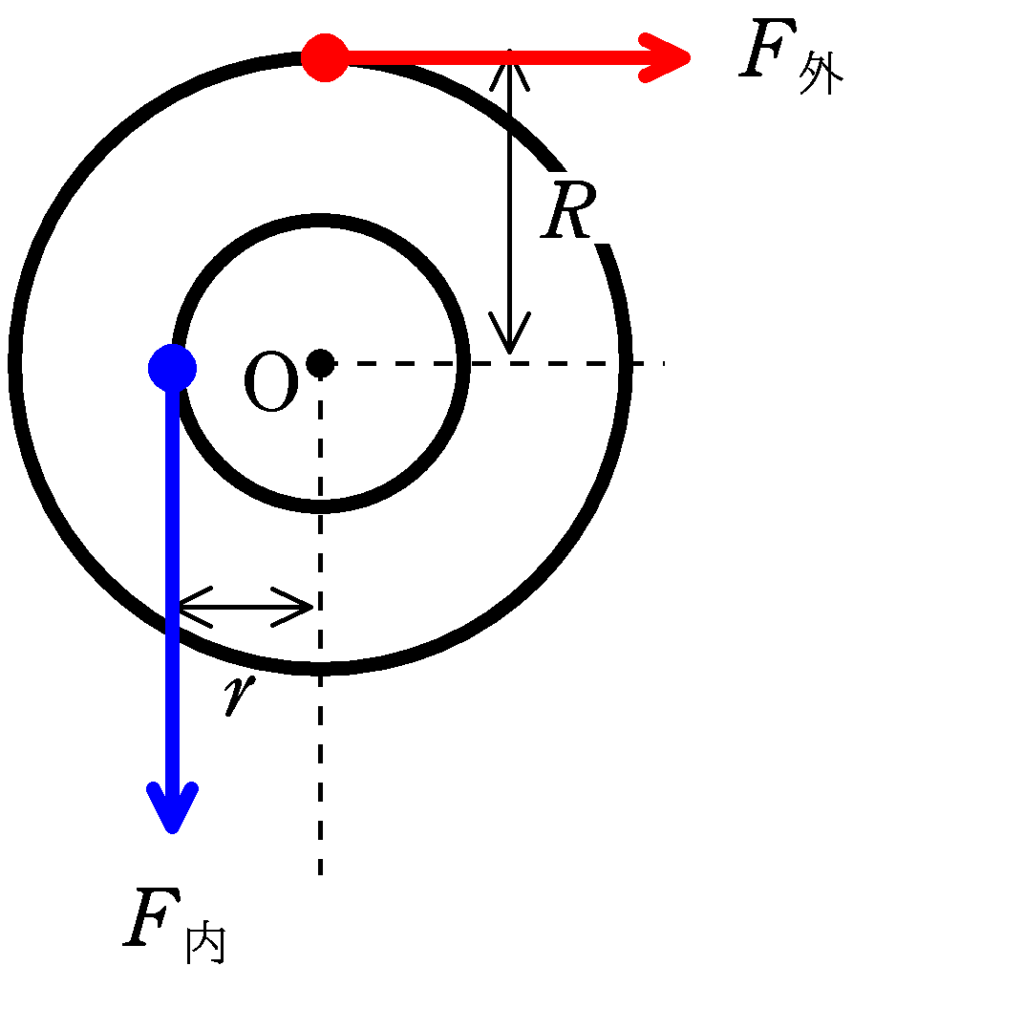
輪軸$\rm O$を中心とします.$\rm O$を中心とすると,時計回りに大きさ$R\times F_{外}$のモーメントと反時計回りに$r\times F_{内}$の力のモーメントのつり合いの式より
★ 力のモーメントのつり合いの式
$R\times F_{外}=r\times F_{内}$ $\therefore\,\, F_{外}:F_{内}=r:R$
外輪と内輪の回転角は同じであることを利用して移動距離の比を求める.

定滑車は糸を引っ張ると,滑車が糸から張力を受けることで回転し,反対側にある糸の物体を持ち上げます.外輪と内輪の半径が異なる場合でも,滑車自体が回転しているので外輪と内輪の回転の角度は一緒です.
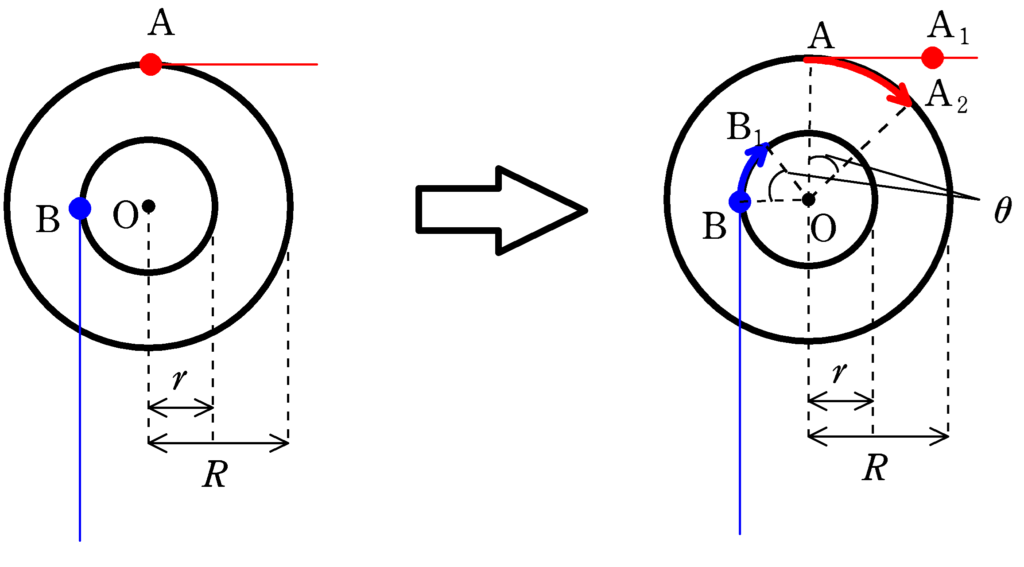
図のように,糸と外輪が接している場所である$\rm A$と糸と内輪が接している$\rm B$に着目してみましょう.
外輪側の糸を長さ$X$分引っ張ったとしましょう.糸の$\rm A$の部分が,$\rm A_{1}$にしたとき,滑車は$\rm A_{2}$まで回転しています.$X$と弧$\rm AA_{2}$の長さは等しいので
(円弧の長さ)$=$(半径)$\times $(中心角)

の関係(ただし,角度は弧度法で表された角度)から回転した角度を$\theta$として
$X=R\theta$ $\cdots (\ast)$

が成り立ちます.一方,滑車が$\theta$回転したの,内輪側の糸が$\theta$分巻かれます.弧$\rm BB_{1}$の長さを$x$とすると,
$x=r\theta$ $\cdots (2\ast)$

が成り立ち,$(2\ast)$から$\theta=\dfrac{x}{r}$とし,$(\ast)$に代入すると
$X=R\times \dfrac{x}{r}$ $\therefore\,\,X:x=R:r$

が成り立ちます.移動距離の比は速さの比と等しく,加速度の比とも等しいので,外輪側と内輪側の加速度の大きさの比も$R:r$となります.

理由がわかると覚えやすいね.


コメント