<問題>
<解答>
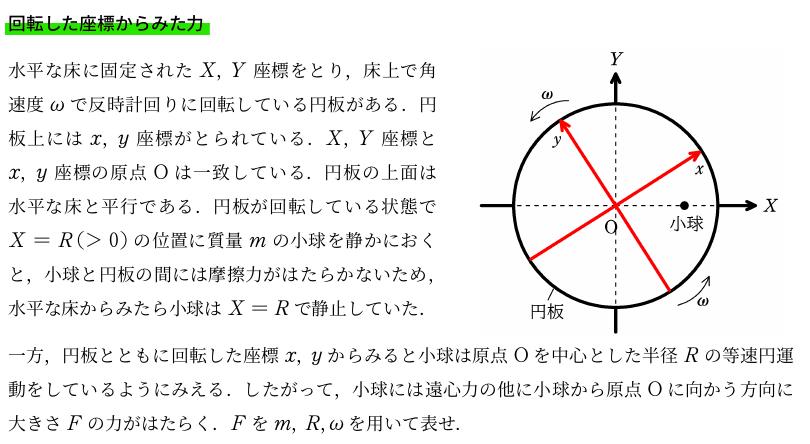
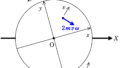
問題文にあるように,静止した床からみると小球が静止しているので,回転した板からみると小球は中心が原点Oで半径$R$の等速円運動をします.
角速度が$\omega$なので,円運動の速さは$R\omega$です.
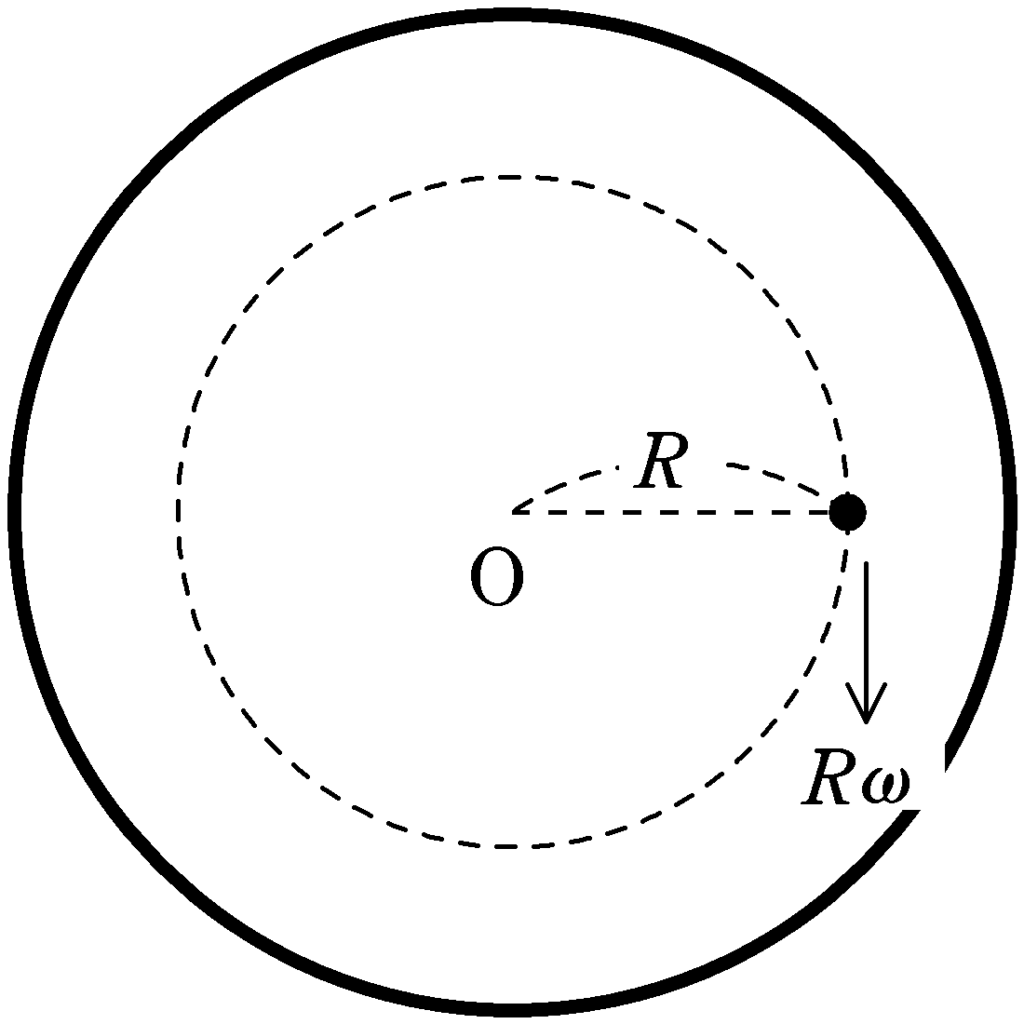
回転した板からみているので,小球からOに向かう方向と逆方向に大きさ$mR\omega^{2}$の遠心力がはたらきます.
半径$r$,円運動の接線方向の速さを$v$,角速度を$\omega$とすると,向心加速度の大きさ$a$は
$a=\dfrac{v^{2}}{r}=r\omega^{2}$
向心加速度の向きは円運動の中心
一方,小球の向心方向の加速度は
$R\omega^{2}$
となります.遠心力だけだと明らかに原点Oに向心力が向きません.そこで,なにかしらの力$F$が原点Oの向きにはたらくはずです.
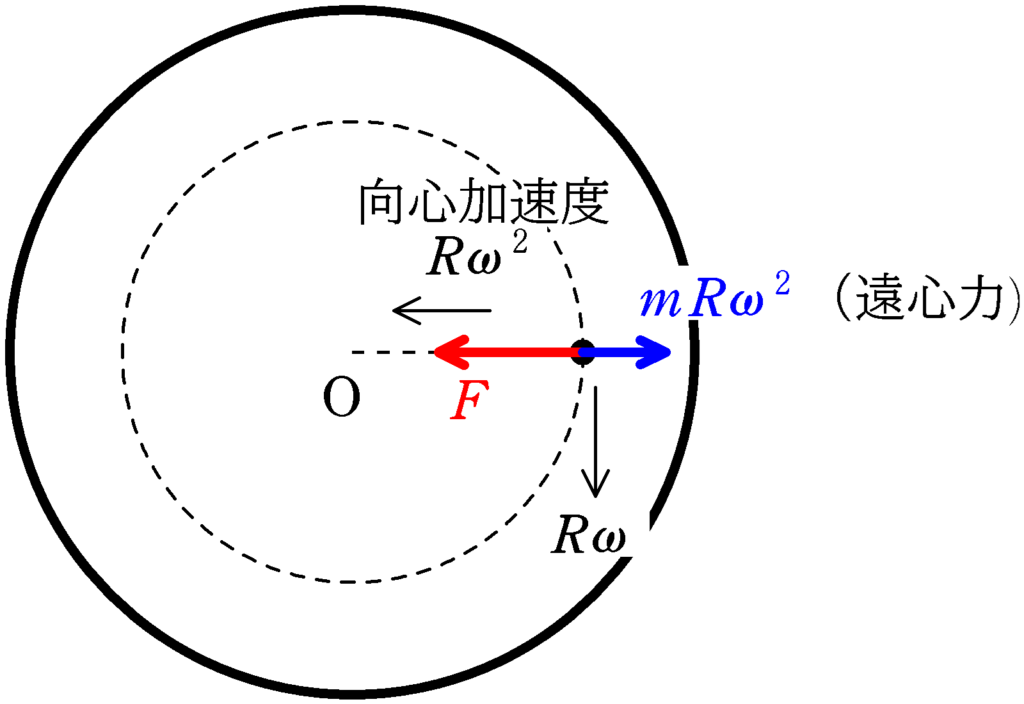
★ 向心方向の運動方程式より
$mR\omega^{2}=F-mR\omega^{2}$
$\therefore\,\, F=2mR\omega^{2}$(答)
この力$F$は一体何なんだという話なのですが,これは高校物理ではできなくともかまいません.(テーマとしては出題されることもあります.)
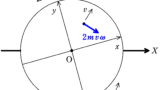
角速度$\omega$で反時計回りに回転する座標(観測者)からみたとき,この観測者からみた質量$m$物体の速さを$v$,とすると,速度の方向より右回り$90^{\circ}$の方向に大きさ
$2mv\omega $
の力がはたらく.この力をコリオリ力(転向力)という.時計回りに回転する座標系の場合は速度の方向より左回りにコリオリ力がはたらく.
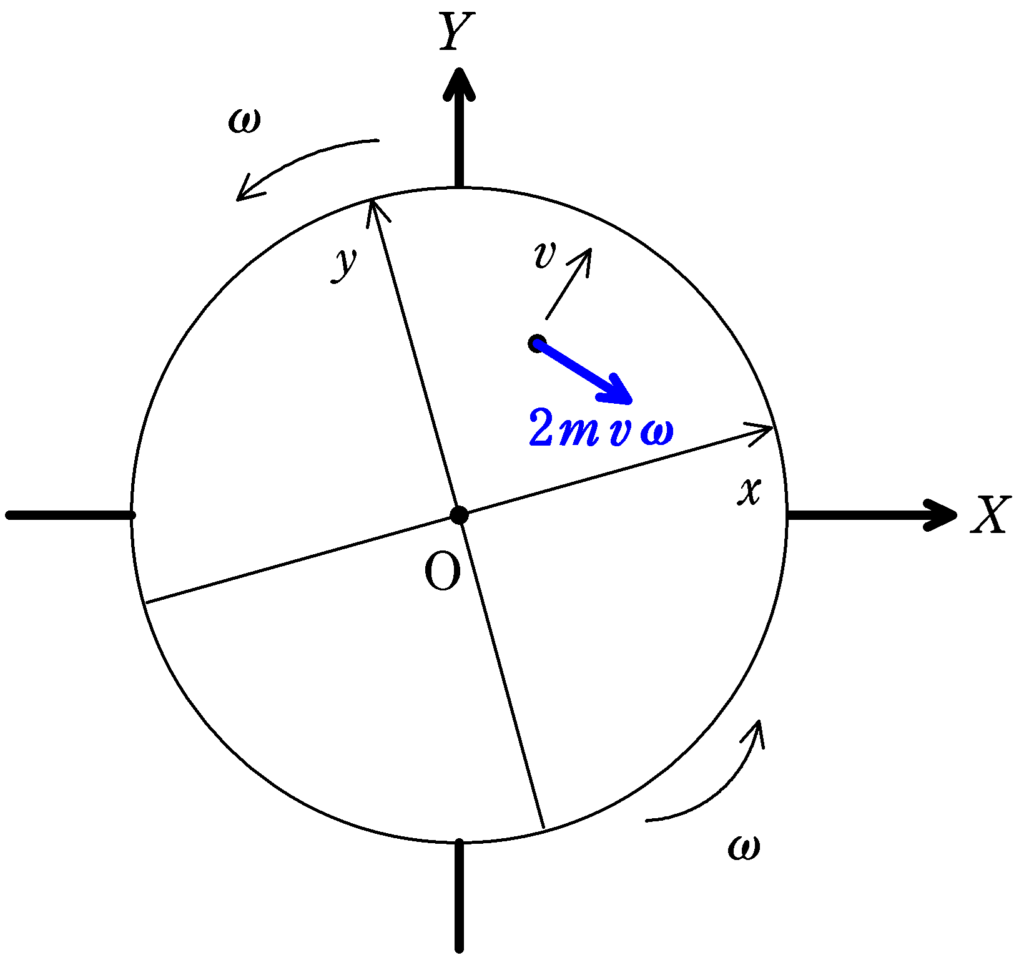
このように,回転した座標からみたときに対象の物体に速度をもつと,遠心力の他に「コリオリ力」という慣性力がはたらきます.
反時計回りに回転した座標からみるとコリオリ力の向きは速度の向きから右回りに90$^{\circ}$の方向でその大きさは
$2mv\omega=2m\times R\omega \times \omega=2mR\omega^{2}$
となり,確かに一致しています.


コメント