<問題>
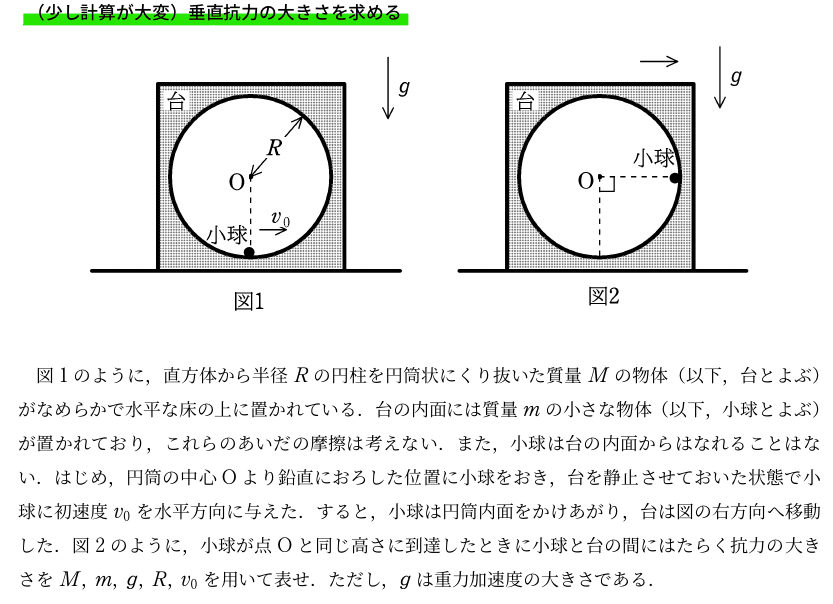
<解答>
最終目標は小球と台の間の抗力の大きさを求めることです.未知な力を求めるということで,運動方程式を立てると予想できるでしょう.
台は水平方向に運動しています.小球は円運動をしているのですが,「誰から見るか?」が大切です.これから立てる運動量保存則,力学的エネルギー保存則は床で静止した人からみた速度を用いますが,小球は「台からみて」Oを中心とした円運動をしています.「静止した床からみる」とOを中心とした円運動にはならないので注意してくだい.
台からみると円運動をするということで,台からみた円の接線方向の速度が欲しくなります.この手の問題は保存則(運動量保存則と力学的エネルギー保存則)を立てて速度を求め,台と,台からみた小球の向心方向の運動方程式を立てることで垂直抗力の大きさを求めていきます.
★ 運動量保存則と力学的エネルギー保存則
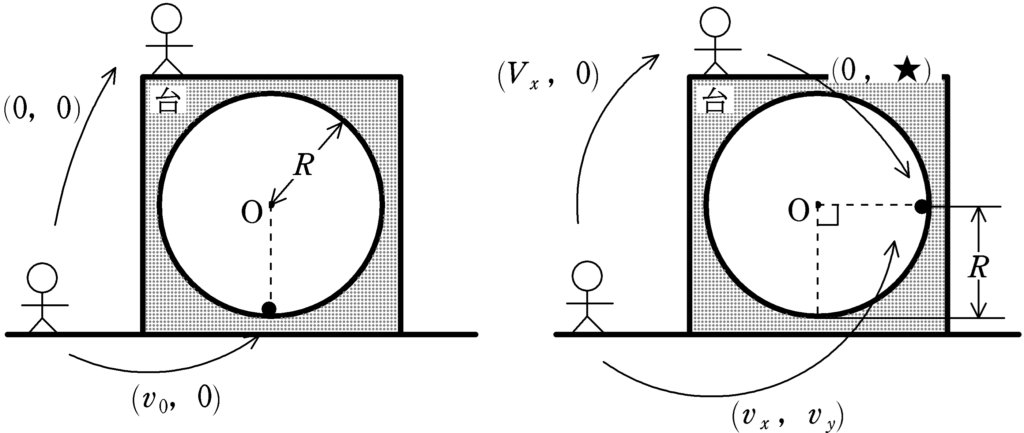
はじめ,小球の速度は$(v_{0},0)$で,台の速度は$(0,0)$です.※速度の表示は$(右向き速度,上向き速度)$です.
また,小球がOと同じ高さにきたとき,床からみた小球の速度を$(v_{x},v_{y})$,台の速度を$(V_{x},0)$とします.台から小球をみると,右方向の速度は$0$なので,上向き速度を★として$(0,★)$とすることができます.すると,速度の関係から
$(V_{x},0)+(0,★)=(v_{x},v_{y})$
より,$v_{x}=V_{x}$,$★=v_{y}$を得ます.$v_{x}=V_{x}$として,床からみたときの水平方向の運動量保存則と,力学的エネルギー保存則より
\begin{align} \begin{cases} mv_{0}=mv_{x}+Mv_{x} &\cdots (\ast)\\ \dfrac{1}{2}mv_{0}^{2}=\dfrac{1}{2}m(v_{x}^{2}+v_{y}^{2})+\dfrac{1}{2}Mv_{x}^{2}+mgR &\cdots (2\ast) \end{cases} \end{align}
$(\ast)$より,$v_{x}=\dfrac{m}{M+m}v_{0}$で,これを$(2\ast)$に代入して,$v_{y}^{2}$を求めます.まず,$(2\ast)$を整理して
\begin{align} &\dfrac{1}{2}(M+m)v_{x}^{2}+\dfrac{1}{2}mv_{y}^{2}+mgR=\dfrac{1}{2}mv_{0}^{2}\\ &\therefore\,\,v_{y}^{2}=v_{0}^{2}-2gR-\dfrac{M+m}{m}v_{x}^{2} \end{align}
$v_{x}=\dfrac{m}{M+m}v_{0}$を代入して
\begin{align} v_{y}^{2}&=v_{0}^{2}-2gR-\dfrac{\cancel{M+m}}{\bcancel{m}}\times \dfrac{m^{\bcancel{2}}}{(M+m)^{\cancel{2}}}v_{0}^{2}\\ &=v_{0}^{2}-2gR-\dfrac{m}{M+m}v_{0}^{2}\\ &=\dfrac{M}{M+m}v_{0}^{2}-2gR \cdots (3\ast) \end{align}
★ 運動方程式
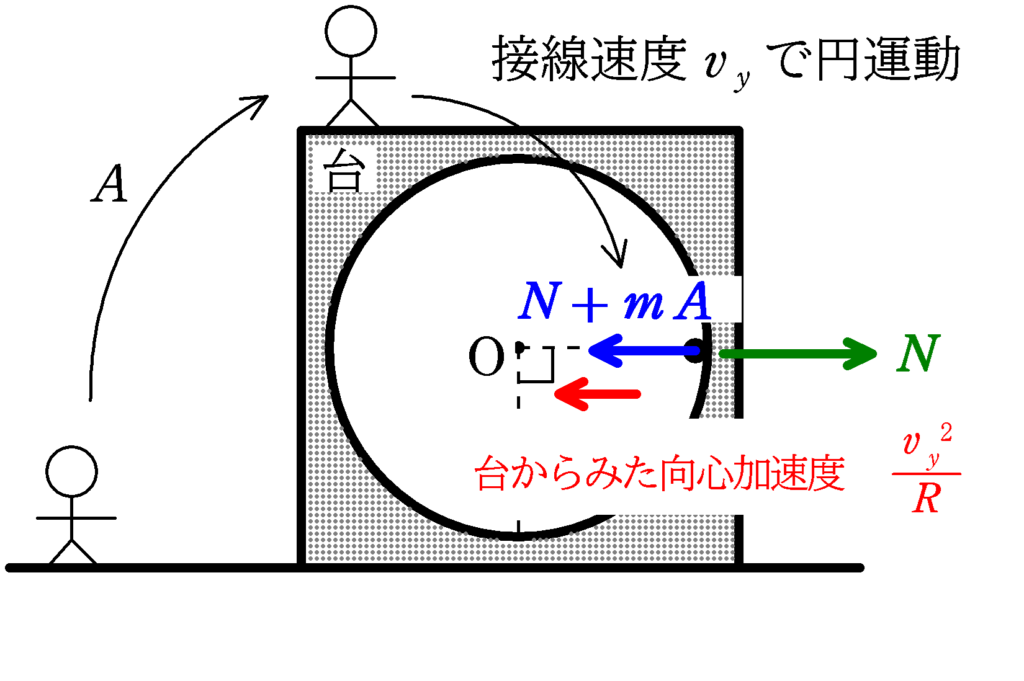
台の水平右向きの加速度を$A$,台と小球の間にはたらく垂直抗力の大きさを$N$としましょう.
台からみた小球はOを中心として接線速度$v_{y}$で半径$R$の円運動をしています.向心加速度は
$\dfrac{v_{y}^{2}}{R}$
であり,台からみているので,垂直抗力以外にも慣性力が左向きに$mA$はたらくことに注意してください.
台の水平方向の運動方程式と台からみた小球の向心方向の運動方程式より
\begin{align} \begin{cases} MA=N &\cdots (4\ast)\\ m\dfrac{v_{y}^{2}}{R}=N+mA &\cdots (5\ast) \end{cases} \end{align}
$(4\ast)$より,$A=\dfrac{N}{M}$とし,$(5\ast)$に代入して$N$を求めていきます.
\begin{align} &m\dfrac{v_{y}^{2}}{R}=N+m\times \dfrac{N}{M}=\dfrac{M+m}{M}N\\ &\therefore\,\, N=\dfrac{M}{M+m}\times \dfrac{mv_{y}^{2}}{R} \cdots (6\ast) \end{align}
$(6\ast)$に$(3\ast)$の$v_{y}^{2}=\dfrac{M}{M+m}v_{0}^{2}-2gR$を代入して
\begin{align} N&=\dfrac{M}{M+m}\times \dfrac{m}{R}\times \left(\dfrac{M}{M+m}v_{0}^{2}-2gR\right)\\ &=\dfrac{Mm}{(M+m)R}\left(\dfrac{M}{M+m}v_{0}^{2}-2gR\right) \textcolor{red}{\bf{(答)}} \end{align}



コメント