高校物理ポイントまとめ集[熱力学編]

1. 可動部分のつり合いの式　→　力の情報が出てくる
2. 理想気体の状態方程式（ボイルシャルルの法則）
3. 熱力学第一法則　→　エネルギーの情報が出てくる

内部エネルギーの変化を$\Delta U$，気体が吸収する熱量を$Q$，気体がした仕事を$W$とすると

$Q=\Delta U+W$

理想気体について，物質量$n$が変化しないとき，気体の圧力を$p$，気体の体積を$V$，絶対温度を$T$とすると，

$\dfrac{pV}{T}=$一定

が成り立つ．（ボイル・シャルルの法則）

特に，温度が一定のとき

$pV=$一定（ボイルの法則）

圧力が一定のとき

$\dfrac{V}{T}=$一定（シャルルの法則）

が成り立つ．

理想気体では，気体の圧力を$p$，体積を$V$，物質量を$n {\rm mol}$，絶対温度を$T$，気体定数を$R$とすると，次の関係式が成り立つ．

$pV=nRT$

問題分に単原子分子理想気体とかいてあるときは，次のことを使うことができる．

定積モル比熱が$\dfrac{3}{2}R$である．すなわち

内部エネルギー$U$は

$U=\dfrac{3}{2}nRT=\dfrac{3}{2}pV$

内部エネルギーの変化$\Delta U$は

$\Delta U=\dfrac{3}{2}nR\Delta T=\dfrac{3}{2}(p_{2}V_{2}-p_{1}V{1})$

※$n$：物質量，$T$：絶対温度，$p$：圧力，$V$：体積

物質量$n$，絶対温度$T$の内部エネルギーUは，定積モル比熱$C_{V}$を用いて

$U=nC_{V}T$

と表す．このとき，$C_{V}$は比例定数であって，定積変化以外でも上の式は成り立つ．

また，マイヤーの関係

$C_{p}=C_{V}+R$

をつかえば，定圧モル比熱を使って，次のように表すこともできる．

$U=n(C_{p}-R)T$

準静的断熱変化をするとき，理想気体の圧力を$p$，体積を$V$，絶対温度を$T$，比熱比を$\gamma$とする．

ただし，$\gamma$は定積モル比熱$C_{\rm{V}}$と定圧モル比熱$C_{\rm{p}}$を用いて，$\gamma=\dfrac{C_{\rm{p}}}{C_{\rm{V}}}$.

このとき，以下のポアソンの式が成り立つ．

$pV^{\gamma}=$一定　，$TV^{\gamma -1}=$一定

特に，単原子分子理想気体のとき，$C_{\rm{V}}=\dfrac{3}{2}R$，$C_{\rm{p}}=\dfrac{5}{2}R$より，$\gamma=\dfrac{5}{3}$となる．

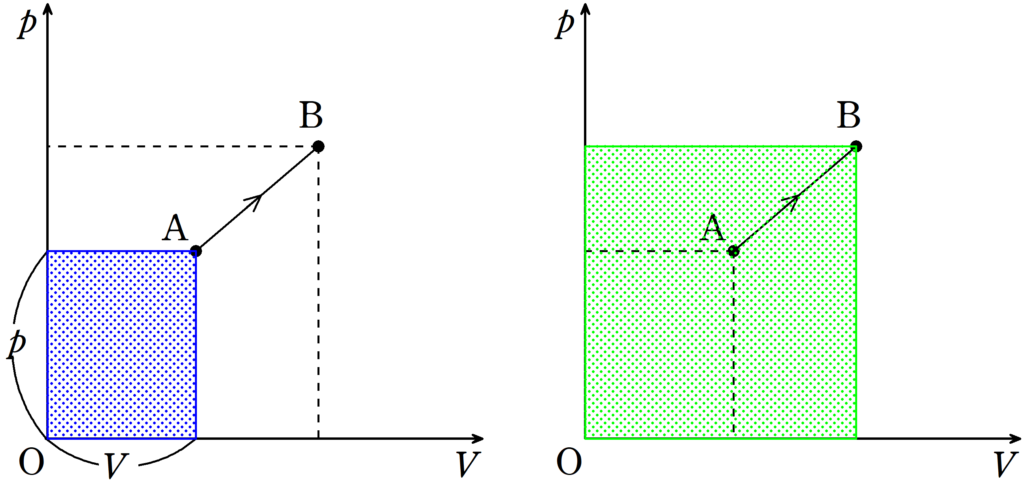
絶対温度は状態の点から$p$軸$V$軸へ下した垂線の足と原点でつくられる長方形の面積に比例する．

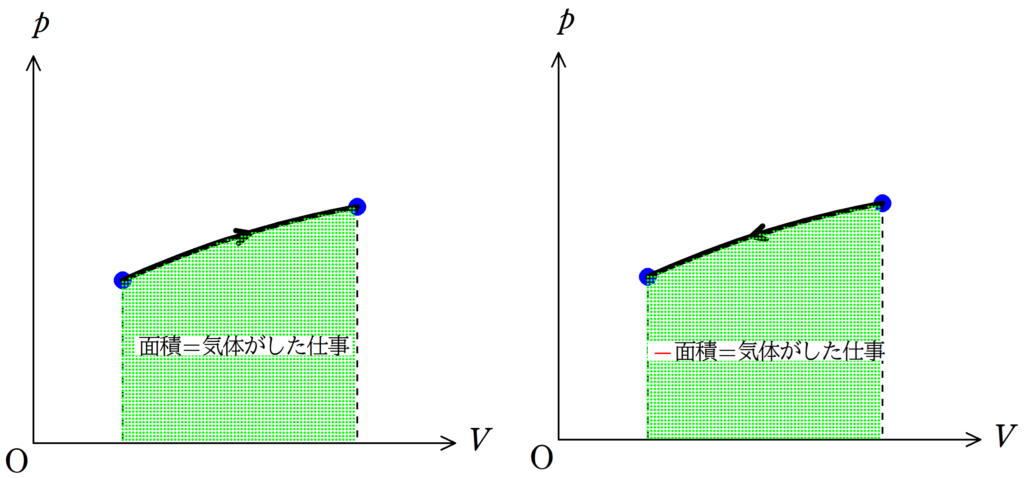
気体がした仕事は上図のように緑色部分の面積を求めることで計算ができる．

ただし，状態変化の矢印が右向きのときは

面積＝気体がした仕事

であるが，状態変化の矢印が左向きのときは

-面積＝気体がした仕事

である．

吸収した熱量を$Q_{\rm{in}}$，放出した熱量を$Q_{\rm_{out}}$，気体が正味のした仕事（気体がした正の仕事，負の仕事を符号付きですべて足すこと）を$W_{気体}$とすると，熱効率$e$は

$e=\dfrac{W_{気体}}{Q_{\rm{in}}}=\dfrac{Q_{\rm{in}}-Q_{\rm{out}}}{Q_{\rm{in}}}=1-\dfrac{Q_{\rm{out}}}{Q_{\rm{in}}}$