
$pV$図において,傾きが負の直線の場合,熱効率を計算するときに注意が必要です.
なぜならば,問題によっては直線の途中で吸熱から放熱に変わることがあるからです.

吸熱から放熱に変わると何か問題があるの?

熱効率の計算の際,分母は吸収した熱量だけを入れなくてはいけないんです.

なるほど!どこまで熱量を吸収したのかがわからないと,熱効率を正確に計算できないんだね.
吸収した熱量を$Q_{\rm{in}}$,放出した熱量を$Q_{\rm_{out}}$,気体が正味のした仕事(気体がした正の仕事,負の仕事を符号付きですべて足すこと)を$W_{気体}$とすると,熱効率$e$は
$e=\dfrac{W_{気体}}{Q_{\rm{in}}}=\dfrac{Q_{\rm{in}}-Q_{\rm{out}}}{Q_{\rm{in}}}=1-\dfrac{Q_{\rm{out}}}{Q_{\rm{in}}}$

そして,やっかいなのが,どこで吸熱から放熱に変わるかの計算は意外と大変なんです.
もし,吸熱から放熱に変わらないのであれば計算がかなり楽なんですが,それを確かめるのもなかなか大変です.
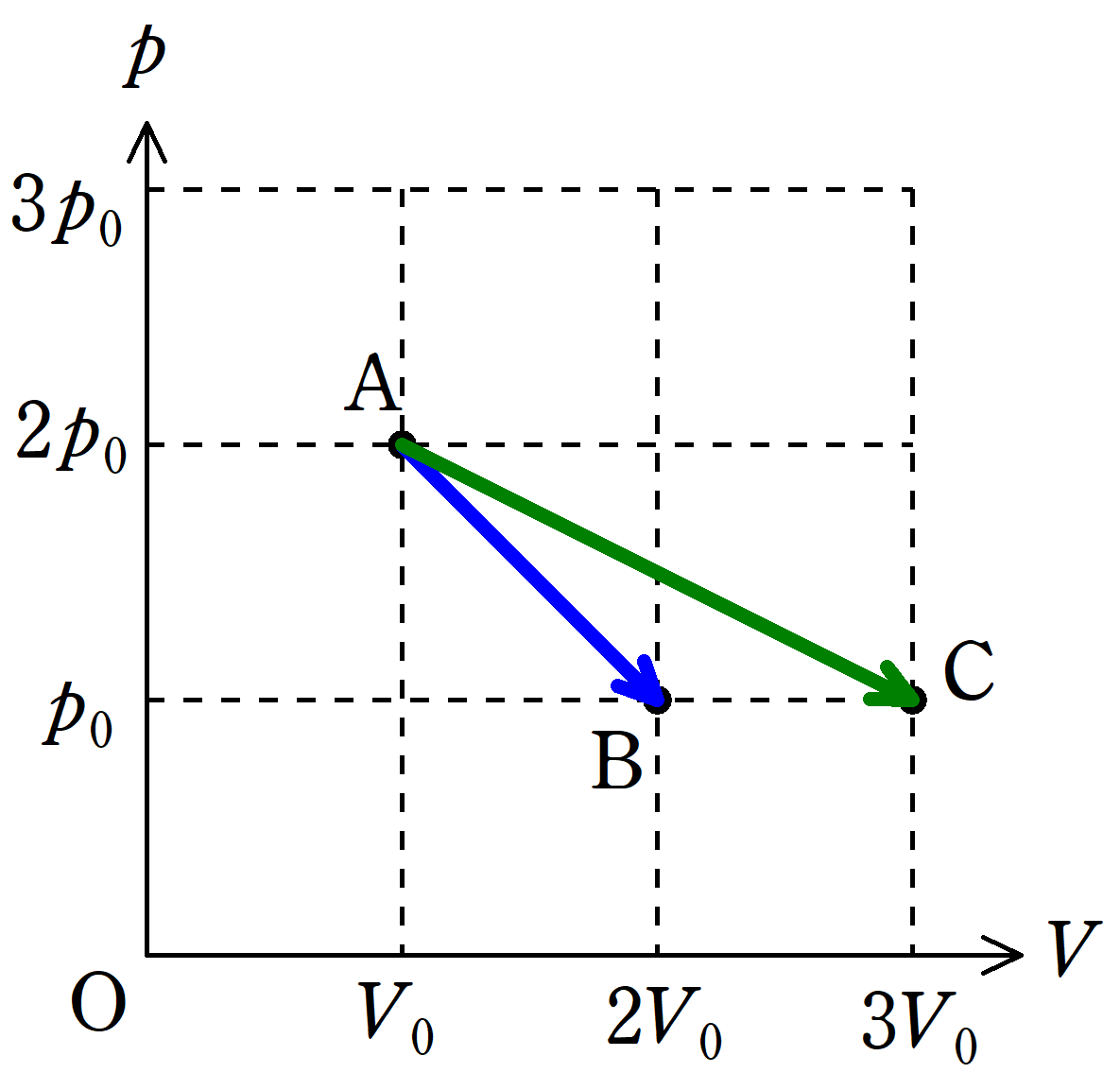
下の記事は吸熱から放熱にかわる一つの例です.

確かに少し大変そうだね.
吸熱から放熱に変わらない条件はない?

あります.
しかし,基本的には覚えておかなくてもいい条件式であることを強調しておきます.
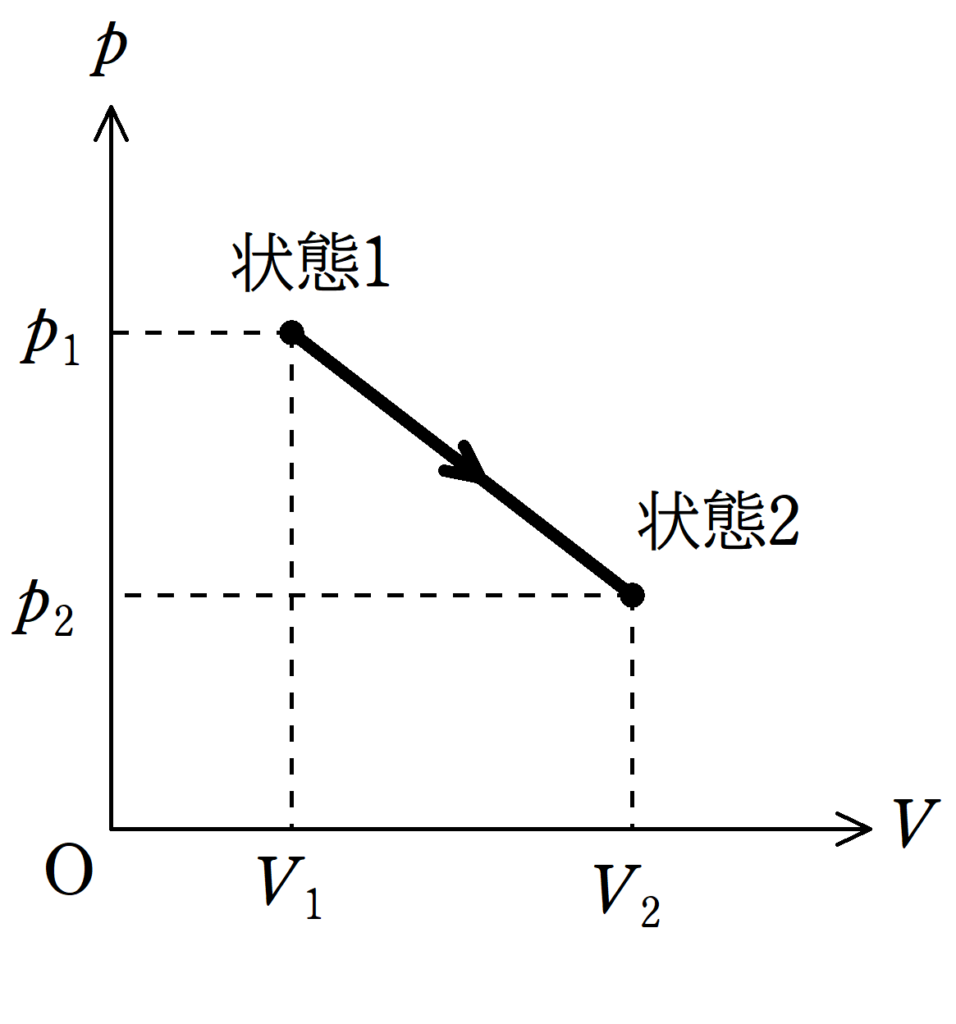
単原子分子理想気体において,体積が$V_{1}$,圧力が$p_{1}$の状態1から体積が$V_{2}$,圧力が$p_{2}$に上図のように直線的に変化する.
また,上図の$pV$図は傾きが負の直線である.
次の不等式を満たすとき,状態1から状態2において,吸熱が放熱に変わらない.
$\dfrac{5(p_{1}V_{2}-p_{2}V_{1})}{8(p_{1}-p_{2})}>V_{2}$
<理由>
状態1から変化をスタートし,体積$V$のとき,圧力を$p$とする.
この直線は$(V_{1} , p_{1})$,$(V_{2} , p_{2})$を通るので
$p-p_{1}=\dfrac{p_{2}-p_{1}}{V_{2}-V_{1}}\left(V-V_{1}\right)$
$\therefore p=-\dfrac{p_{1}-p_{2}}{V_{2}-V_{1}}V+\dfrac{p_{1}V_{2}-p_{2}V_{1}}{V_{2}-V_{1}}$ $\dots (\ast)$
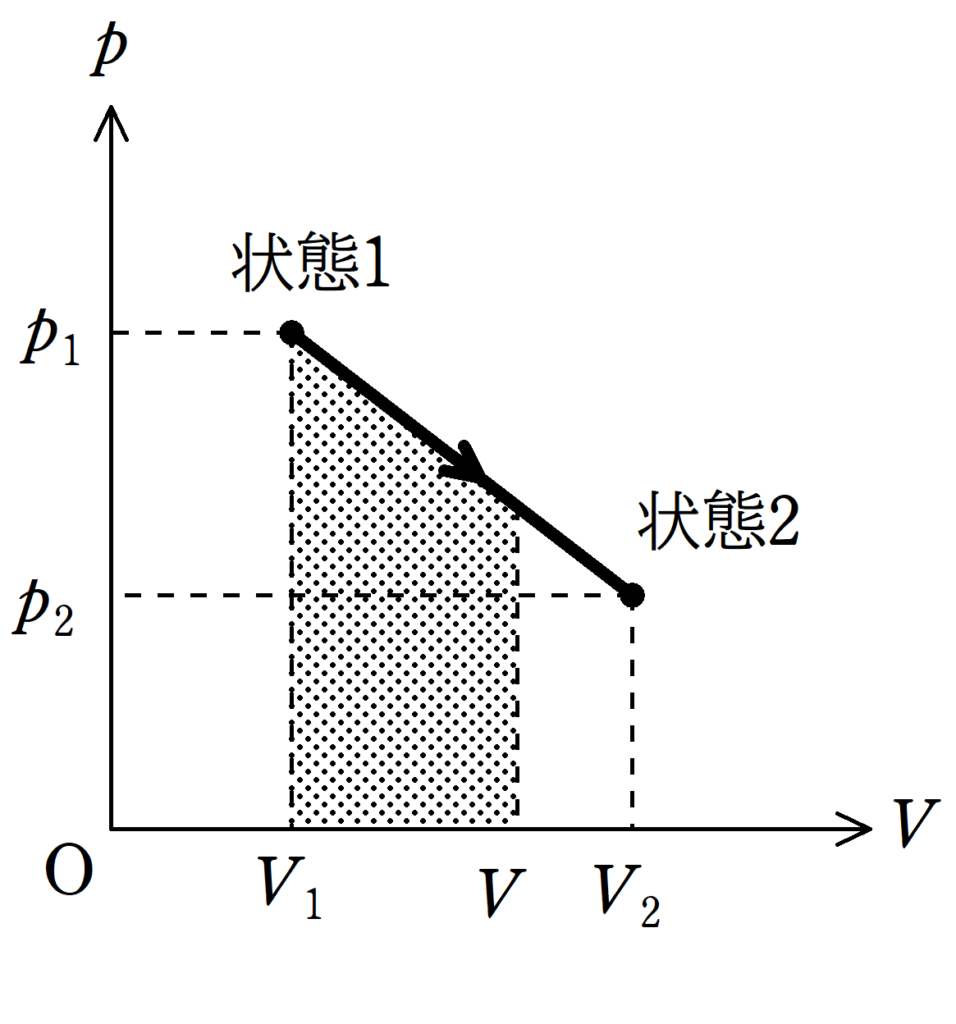
この間に気体がする仕事$W$は
$W=\dfrac{1}{2}\left(p+p_{1}\right)(V-V_{1})$ $\dots (2\ast)$
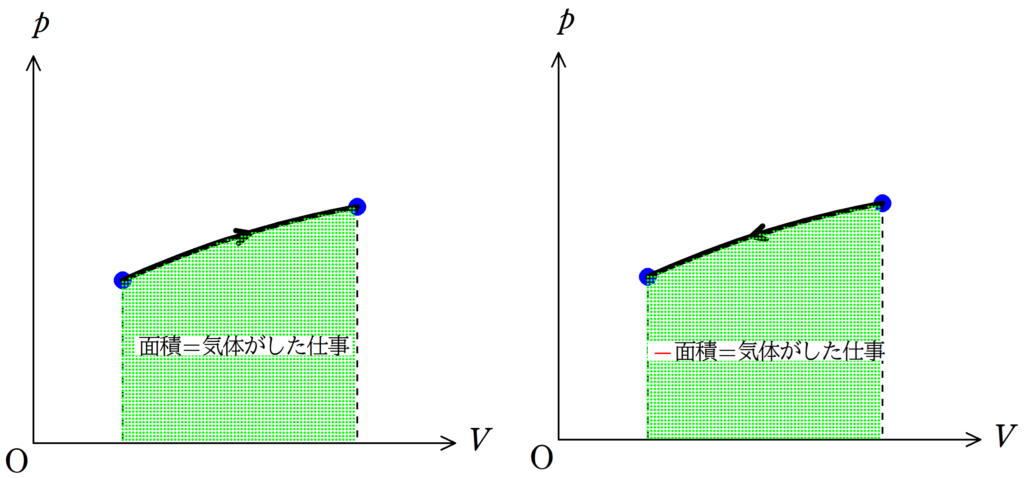
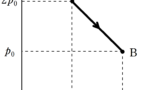
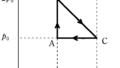
気体がした仕事は上図のように緑色部分の面積を求めることで計算ができる.
ただし,状態変化の矢印が右向きのときは
面積=気体がした仕事
であるが,状態変化の矢印が左向きのときは
-面積=気体がした仕事
である.
また,内部エネルギー変化$\varDelta U$は
$\varDelta U=\dfrac{3}{2}\left(pV-p_{1}V_{1}\right)$ $\dots (2\ast)$
問題分に単原子分子理想気体とかいてあるときは,次のことを使うことができる.
定積モル比熱が$\dfrac{3}{2}R$である.すなわち
内部エネルギー$U$は
$U=\dfrac{3}{2}nRT=\dfrac{3}{2}pV$
内部エネルギーの変化$\Delta U$は
$\Delta U=\dfrac{3}{2}nR\Delta T=\dfrac{3}{2}(p_{2}V_{2}-p_{1}V{1})$
※$n$:物質量,$T$:絶対温度,$p$:圧力,$V$:体積
$(\ast)$,$(2\ast)$と熱力学第一法則より,状態1から体積が$V$になるまでに気体が吸収する熱量$Q$は
$\eqalign{Q&=\varDelta U+W\\&=\dfrac{3}{2}\left(pV-p_{1}V_{1}\right)+\dfrac{1}{2}\left(p+p_{1}\right)(V-V_{1})\\&=\dfrac{1}{2}\left(4pV-pV_{1}+p_{1}V-4p_{1}V_{1}\right)\\&=-\dfrac{2(p_{1}-p_{2})}{V_{2}-V_{1}}V^{2}+\dfrac{5(p_{1}V_{2}-p_{2}V_{1})}{2(V_{2}-V_{1})}V-\dfrac{5p_{1}V_{2}-p_{2}V_{1}-4p_{1}V_{1}}{V_{2}-V_{1}}V_{1}}$
ここで,
$\dfrac{dQ}{dV}=-\dfrac{4(p_{1}-p_{2})}{V_{2}-V_{1}}V+\dfrac{5(p_{1}V_{2}-p_{2}V_{1})}{2(V_{2}-V_{1})}$
より,$\dfrac{dQ}{dV}=0$となる$V$は,
$V=\dfrac{5(p_{1}V_{2}-p_{2}V_{1})}{8(p_{1}-p_{2})}$
ここで,$Q$を縦軸,$V$を横軸としたグラフは

このグラフより,$V=\dfrac{5(p_{1}V_{2}-p_{2}V_{1})}{8(p_{1}-p_{2})}$より前は体積が増えるたびに$Q$が増加し,その後減少に転じる.
したがって,$V=\dfrac{5(p_{1}V_{2}-p_{2}V_{1})}{8(p_{1}-p_{2})}$は吸熱から放熱に変わる体積となる.
これが,$V_{2}$より大きいとき,吸熱から放熱に変わらないので
$\therefore \dfrac{5(p_{1}V_{2}-p_{2}V_{1})}{8(p_{1}-p_{2})}>V_{2}$

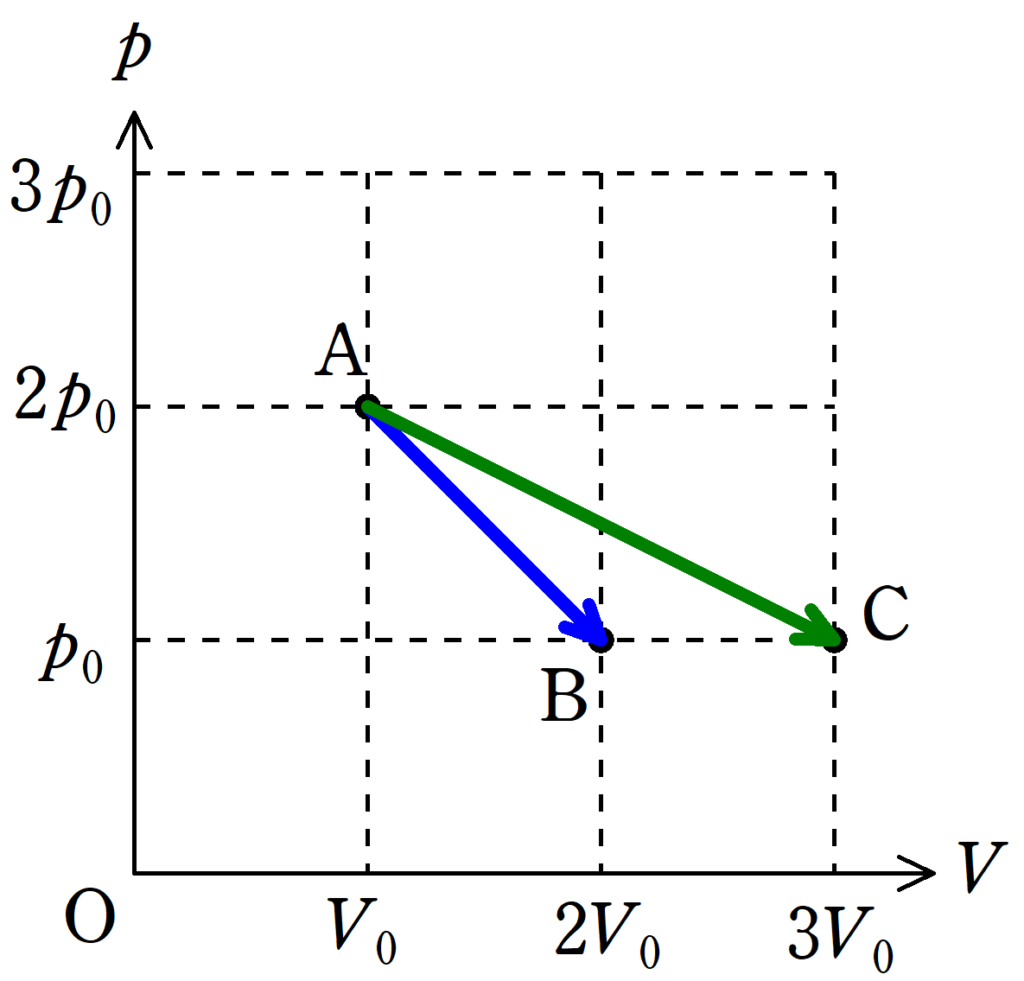
ちなみに,下図の青色の直線は途中から放熱に変わり,緑色の直線は吸熱のままです.


コメント