2024年の東工大,大問1は東工大の中でもなかなか取り組みにくい問題でした.問題に書かれていることにしたがっていけば解けなくはないですが,「なぜそのように考えていいのか?」がよくわからず,モヤモヤしたまま解く人も多かったんじゃないかと思います.
この記事では,その中でも理解しにくい[C]の小球の円運動についての説明をしていきます.
詳しい問題の設定はここにのせないのでご了承ください。
疑問点の確認
[C]の問題文の一部を引用すると次のようなことが書かれています.
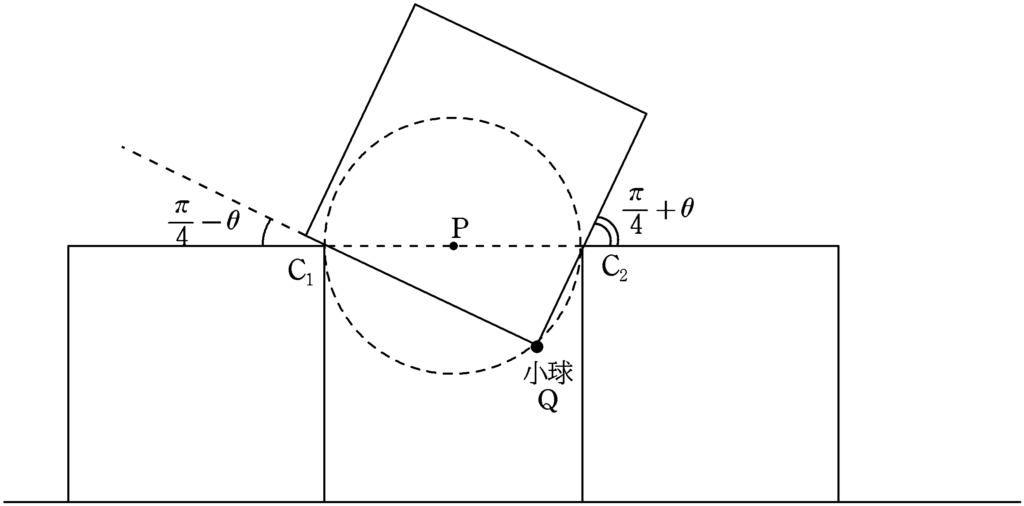
[C] ….$M$が十分大きく,$\rm B_{1}$と$\rm B_{2}$のいずれも静止したままである場合には,小球は床からの高さ$l$の点Pを中心として単振り子と同じ運動をする.
2024年東京工業大入試問題
ここで,疑問点を整理すると,
1.なぜ小球は円運動するのか.
2.(h)は小球の向心方向の運動方程式を立てて解くが,なぜ小球に$\rm B_{1},B_{2}$が$\rm A$に及ぼす垂直抗力の合力$G$がはたらくのか.
3.なぜ合力$G$は$\rm P$の方向に向くのか.
以上3点を解説していきます.
1.なぜ小球は円運動するのか.
この答えは簡単です.立方体$\rm B_{1}$と立方体$\rm A$の接点を$\rm C_{1}$,立方体$\rm B_{2}$と立方体$\rm A$の接点を$\rm C_{2}$とします.また,小球の位置を点$\rm Q$とします.すると,常に
$\angle{\rm C_{1}QC_{2}}=\dfrac{\pi}{2}$

が成り立つから,「円周角の定理の逆」より,$\rm Q$は点$\rm P$を中心とした半径$\dfrac{l}{2}$の円上を動きます.
2.(h)は小球の向心方向の運動方程式を立てて解くが,なぜ小球に$\rm B_{1},B_{2}$が$\rm A$に及ぼす垂直抗力の合力$G$がはたらくのか.
問(h)の合力$G$を求める際に小球の向心方向の運動方程式を立てることで問題を解きます.その際に,小球にはたらく力として,$G$と重力がはたらくとしているのですが,小球に直接$G$がはたらいている感じはしません.
あくまでも$G$を受けるのは立方体$\rm A$です.このことについて解説します.
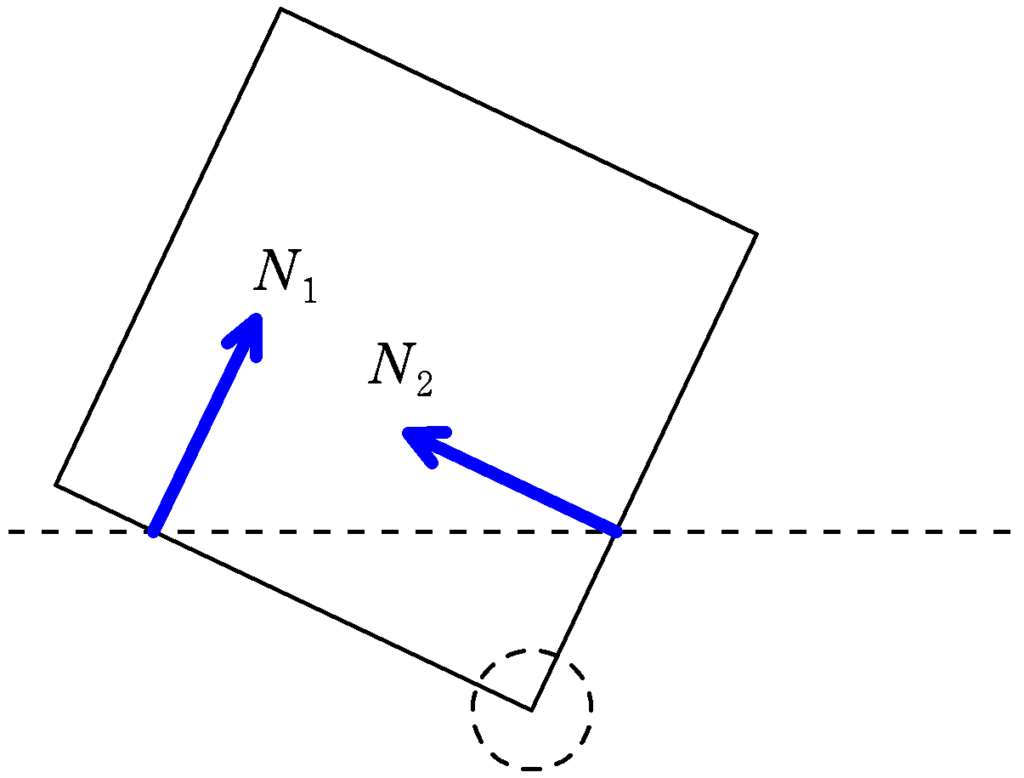
まず,立方体$\rm A$には,$\rm B_{1},B_{2}$から垂直抗力$N_{1},N_{2}$がはたらきます.($N_{1},N_{2}$はこちらで設定したものです)
ここで,立方体は「質量を無視できる」ので,どのような運動をしていようと「力がつり合っています」
運動方程式$ma=F$において,$m=0$なら,$F=0$
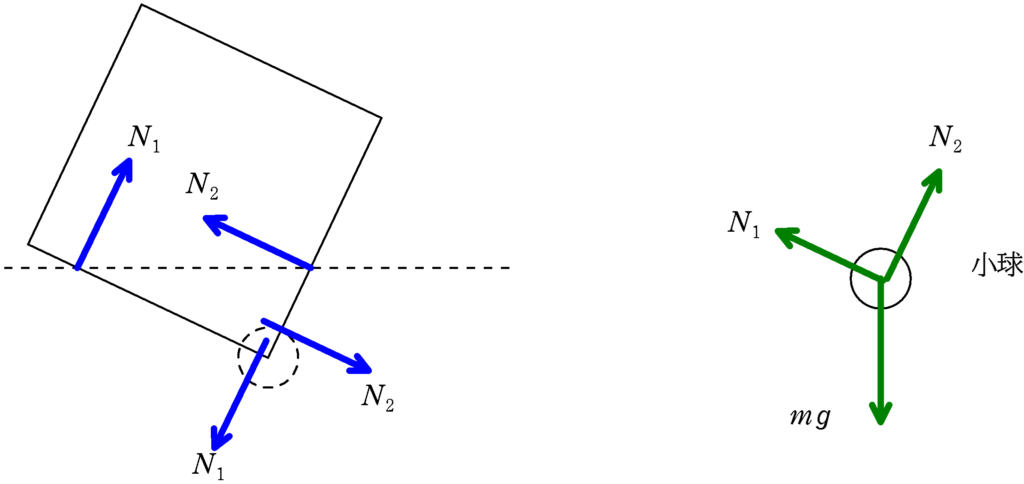
小球が立方体$\rm A$におよぼす力は立方体$\rm A$がつり合うように,$N_{1}$と大きさが同じで反対方向に,同じく$N_{2}$と大きさが同じで反対方向に力を及ぼします.(上図の点線○が小球がある位置です)
すると,作用反作用の法則より,小球には右上図のような力,つまり重力$mg$と$N_{1},N_{2}$がはたらくことになります.
この$N_{1},N_{2}$は結局$\rm B_{1},B_{2}$が$\rm A$におよぼす力と同じ大きさ同じ向きになります.
つまり,小球には重力$mg$と合力$G$がはたらくことは正しいということです.
3.なぜ合力$G$は$\rm P$の方向に向くのか.
最後になぜ合力$G$は点$\rm P$の方向,つまり小球の円運動の接線と垂直な方向にはたらくのか,です.
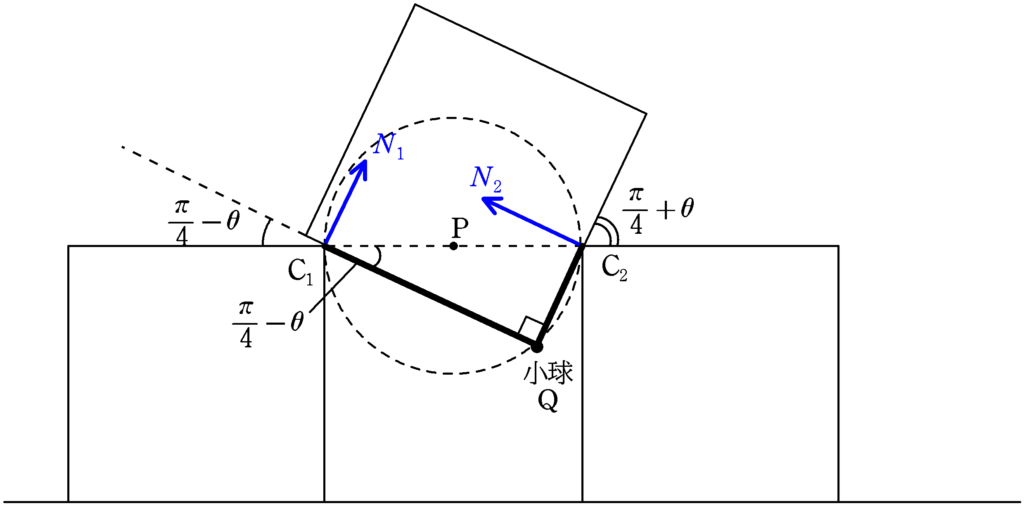
まず,$N_{1}$と$N_{2}$の大きさの比から求めていきたいと思います.立方体$\rm A$を対象にして点$\rm Q$まわりの力のモーメントのつり合いの式を立てます.(立方体$\rm A$は質量を無視できるので,回転していても力のモーメントの和はゼロになります.)
上図において,三角形$\rm C_{1}QC_{2}$を考えると,${\rm C_{1}C_{2}}=l$であるから
${\rm C_{1}Q}=l\cos\left(\dfrac{\pi}{4}-\theta \right)$
${\rm C_{2}Q}=l\sin\left(\dfrac{\pi}{4}-\theta \right)$
★力のモーメントのつり合いの式より
$l\cos\left(\dfrac{\pi}{4}-\theta \right)\times N_{1}=l\sin\left(\dfrac{\pi}{4}-\theta \right)\times N_{2}$
よって,
$N_{1} : N_{2}=\sin\left(\dfrac{\pi}{4}-\theta \right):\cos\left(\dfrac{\pi}{4}-\theta \right)$
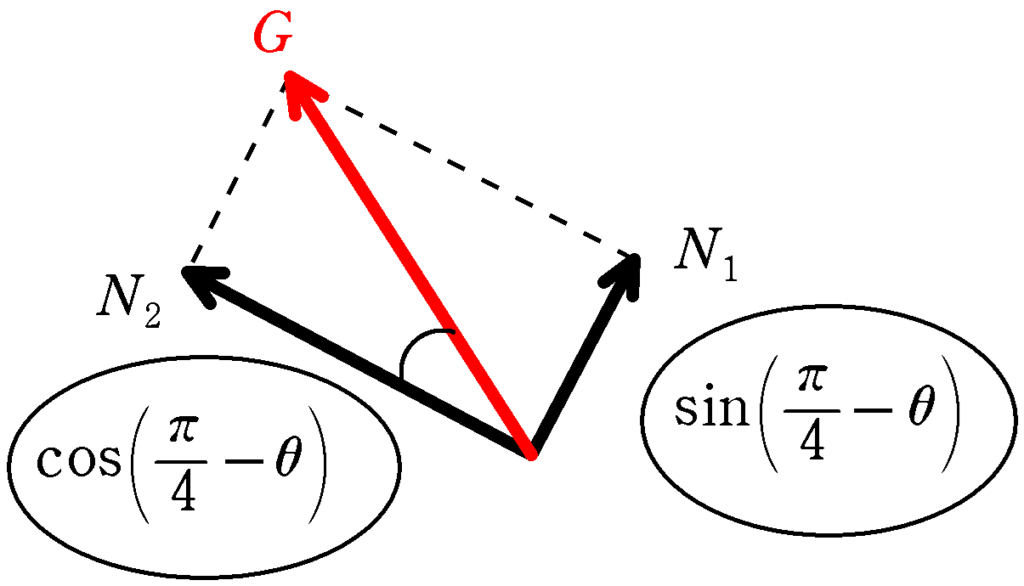
このことから,$G$と$N_{2}$のなす角は$\dfrac{\pi}{4}-\theta$であることがわかります.
もし$\rm C_{1}Q$と$\rm PQ$のなす角が$\dfrac{\pi}{4}-\theta$であれば,$G$は$\rm Q$から$\rm P$の方向を向くことがわかります.調べていきましょう.
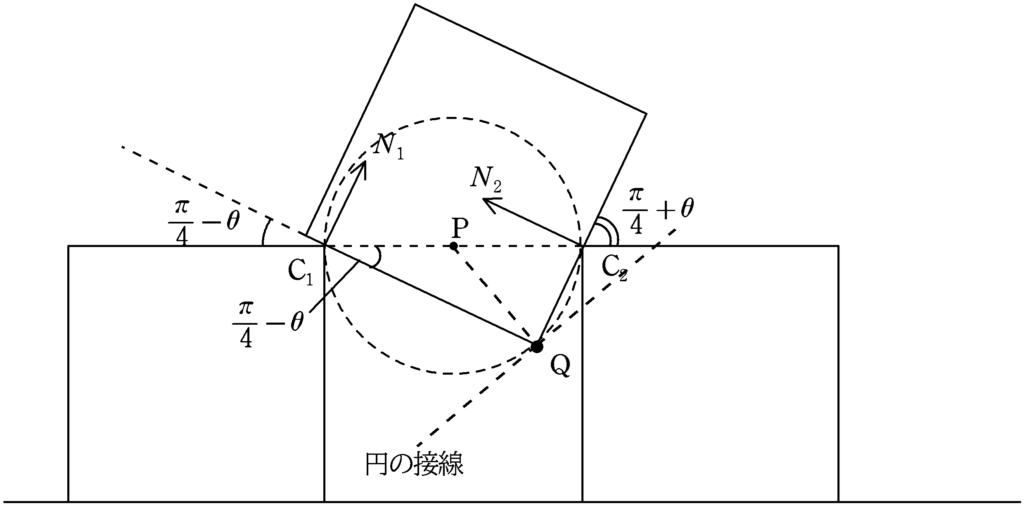
上図では$\rm P$と$\rm Q$を結び,$\rm Q$における円の接線をかきました.
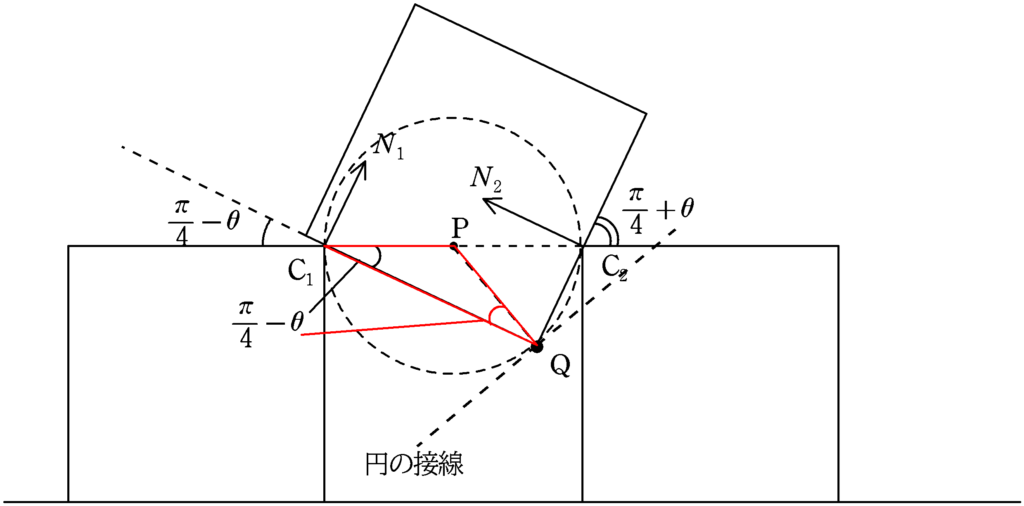
ここで,三角形$\rm C_{1}PQ$に着目すると,この三角形は$\rm PC_{1}=PQ$の2等辺三角形でなので,$\angle{\rm PC_{1}Q}=\angle{\rm C_{1}QP}=\dfrac{\pi}{4}-\theta$となります.
つまり,確かに$G$は$\rm Q$から$\rm P$の方向を向くわけです.
おわり
今までの考察から,小球には重力$mg$と垂直抗力の合力$G$がはたらき,$G$は常に$\rm P$に向くことがわかりました.
これは点$\rm P$と点$\rm Q$が糸でつながれていて単振り子運動しているときと全く同じように考えることができるわけです.


コメント